数学建模中的插值与拟合技术解析
版权申诉
55 浏览量
更新于2024-07-01
收藏 2.62MB PPT 举报
"插值和拟合是数学建模中常用的技术,用于通过有限的数据点构建连续函数。本文主要讨论了一维和二维插值方法,包括MATLAB中的插值函数和示例。"
插值是一种在给定离散数据点间构造函数的方法,目的是找到一个尽可能接近这些点的光滑函数。在数学建模中,插值常用于估算未知数据点的值或创建平滑曲线来代表离散数据集。插值方法有多种,如最邻近插值、线性插值、三次样条插值和立方插值。
一维插值在MATLAB中通常使用`interp1`函数实现。这个函数接受四个参数:`x`是插值节点,`y`是在这些节点上的被插值点,`xi`是要进行插值的新的自变量值,`method`指定了插值方法。默认方法是线性插值,但也可以选择`nearest`(最邻近插值)、`spline`(三次样条插值)或`cubic`(立方插值)。所有方法都需要`x`是单调的,且`xi`不能超出`x`的范围。
Runge现象是一个在插值过程中可能出现的问题,即当插值节点过于集中在某些区域时,插值函数可能会出现剧烈波动,导致不准确的结果。三次样条插值通常可以提供更平滑的插值曲线,避免Runge现象。
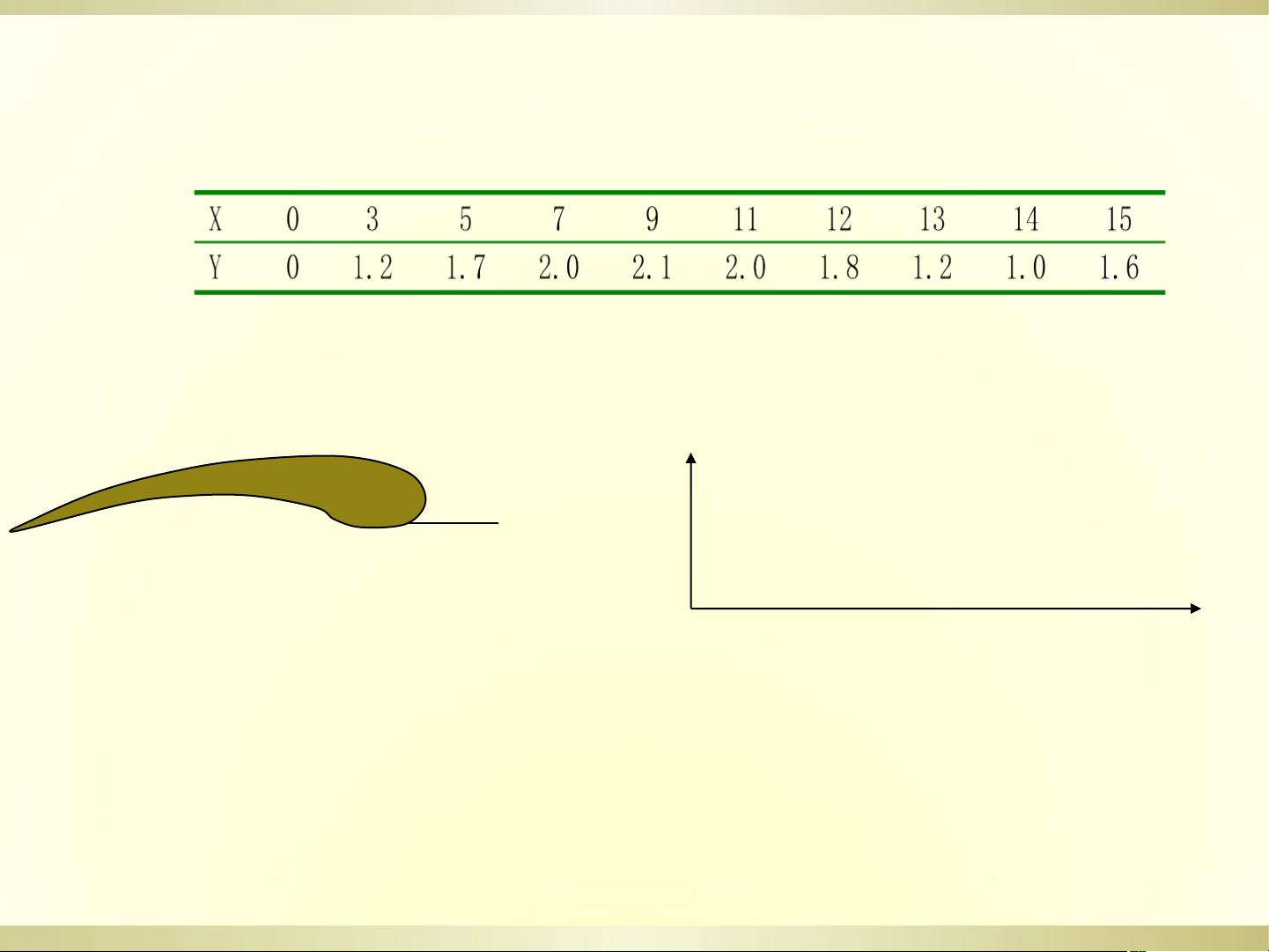
在提供的例子中,例1展示了使用三次样条插值 (`'spline'`) 的过程,比较了插值函数与原始函数的接近程度。例2说明了如何利用插值来估计温度变化,其中数据点每隔1小时测量一次,通过`spline`插值可以估计出每1/10小时的温度。例3涉及飞机机翼下轮廓线的数据插值,分别使用线性和三次样条插值来计算当`x`每改变0.1时对应的`y`值,展示了不同插值方法的效果差异。
二维插值类似,但通常处理的是多维数据,例如在地理信息系统或图像处理中。尽管此处未详细介绍,但MATLAB的`interp2`函数可以用于二维插值任务。
插值和拟合是数据分析和建模中的关键工具,它们能够帮助我们理解和预测数据趋势,尤其是在数据点稀疏或者需要平滑曲线的情况下。理解并熟练运用各种插值方法,对于处理实际问题具有重要意义。
2022-01-18 上传
2009-10-07 上传
2021-10-03 上传
2021-10-09 上传
129 浏览量
112 浏览量
卷积神经网络
- 粉丝: 376
最新资源
- 易语言开发的115网盘信息读取模块教程
- 高效开发插件必备:org.eclipse.jdt.rar包解读
- 大屏拼接显示系统V2.3.7控制软件功能解析
- AutoCAD2010机械制图核心教程完整版
- swspec:探索C语言编写的软件光谱仪
- YQLightLable:仿iOS解锁动画的自定义Label组件
- 易语言实现115下载地址解析方法
- PHP聊天室初学者下载示例
- IIS短文件名泄露漏洞检测工具
- Caffe安装必选:protobuf-2.5.0压缩包使用教程
- iTerm 2 Monokai 主题:Emacs风格颜色方案应用
- regioneR:基于置换测试的基因组区域关联分析工具
- iOS源码:实现登录页面回调与页面刷新
- C# 100多个常用类库快速开发指南
- OC封装图片获取功能,直接调用返回NSData格式
- 易语言实现10进制与16进制转换工具