算法设计：递归动态规划与分治法解析

"这份资料是关于算法设计的期末试卷及答案，主要涵盖了计算机科学（cs）领域的知识，包括递归动态规划、分治法、分支限界法和回溯法等核心算法概念及其应用。" 一、递归动态规划算法与分治法 递归动态规划算法通常用于解决具有重叠子问题和最优子结构的问题，如最长公共子串和0/1背包问题。其基本步骤如下： 1. **最优解性质**：首先，分析问题的结构，确定最优解的性质，即最优解可以通过子问题的最优解来构建。 2. **递归定义最优值**：然后，定义一个状态转移方程，将问题的最优解转化为更小规模子问题的最优值。 3. **自底向上计算**：通过自底向上的方式，从基础情况开始，逐步计算出所有子问题的最优值。 4. **构造最优解**：最后，根据计算过程中的信息，反向构建出原问题的最优解。 分治法，如汉诺塔问题，同样涉及问题的分解和子问题的解决，但子问题是独立的。分治法通常包含以下步骤： 1. **分解**：将原问题拆分为若干个规模较小且相互独立的子问题。 2. **解决**：直接解或递归解子问题。 3. **合并**：将子问题的解合并以获得原问题的解。 二、分治法的典型算法设计模式 该模式适用于处理如归并排序、快速排序等问题，包括以下几个阶段： 1. **基础情况**：如果问题规模小于某个阈值（n0），则直接解决。 2. **分解**：将问题分解为子问题。 3. **递归解决**：递归地解决每个子问题。 4. **合并**：将子问题的解组合为原问题的解。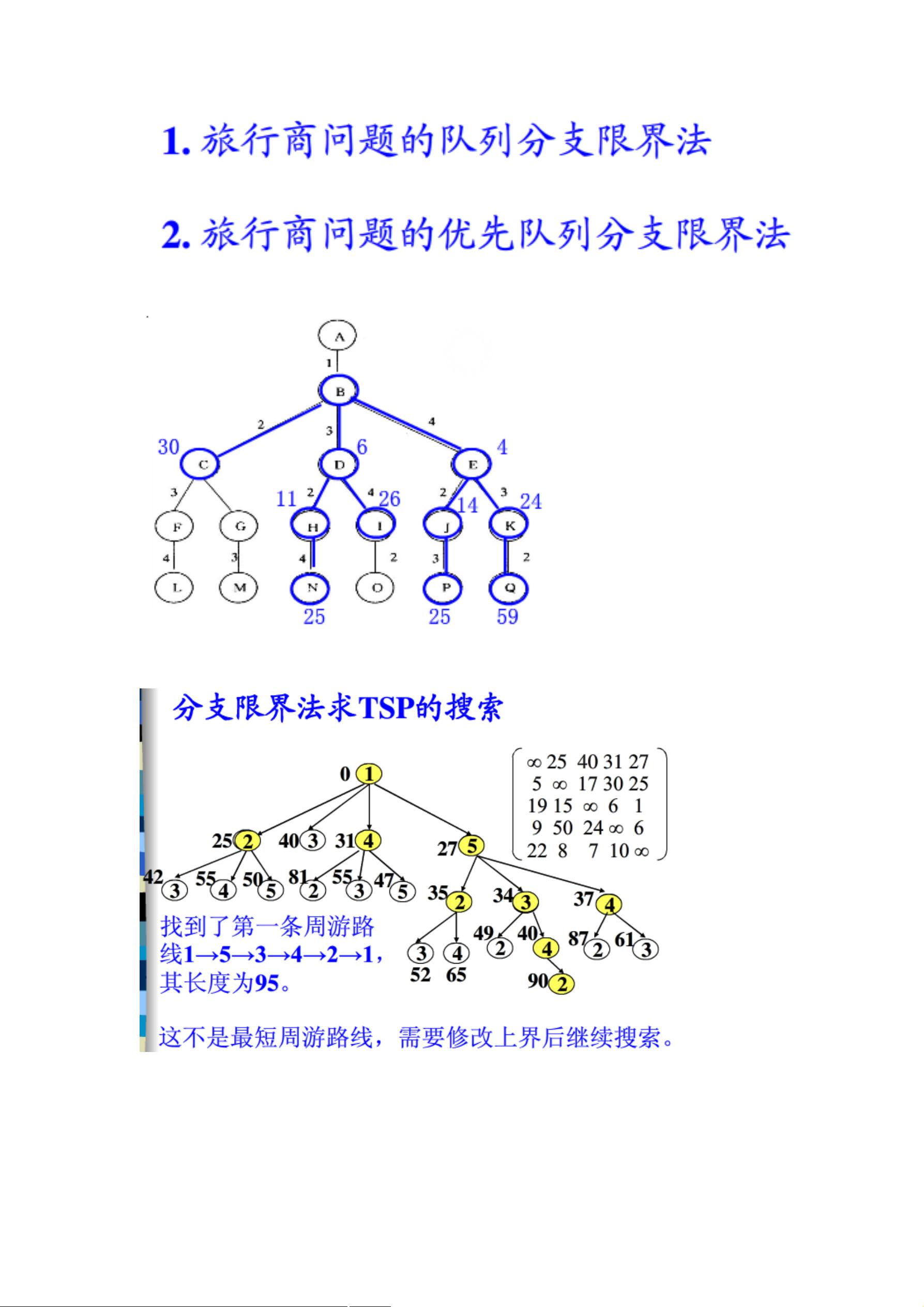 三、分支限界法 分支限界法主要用于解决离散优化问题，如0/1背包和旅行售货员问题。其搜索策略如下： 1. **节点生成**：在当前节点，生成所有可能的儿子节点。 2. **节点选择**：按照某种策略（如优先队列）选择下一个活节点，通常是具有最佳边界函数值的节点。 3. **推进搜索**：通过不断选择最有利节点，向解空间中可能存在最优解的方向进行搜索。 四、回溯法 回溯法是通过深度优先搜索解决约束满足问题，如八皇后问题等，主要包括： 1. **解空间定义**：明确问题的解空间结构。 2. **搜索策略**：采用深度优先策略搜索解空间。 3. **剪枝函数**：在搜索过程中应用剪枝函数，避免无效路径，提高效率。 通过以上四种方法，可以有效地解决各种复杂的问题，它们在计算机科学领域中具有广泛的应用，如数据结构优化、图形算法、搜索问题和决策制定等。理解并熟练掌握这些算法对于提升编程能力、解决实际问题至关重要。