数据结构详解：Treap的构造与操作

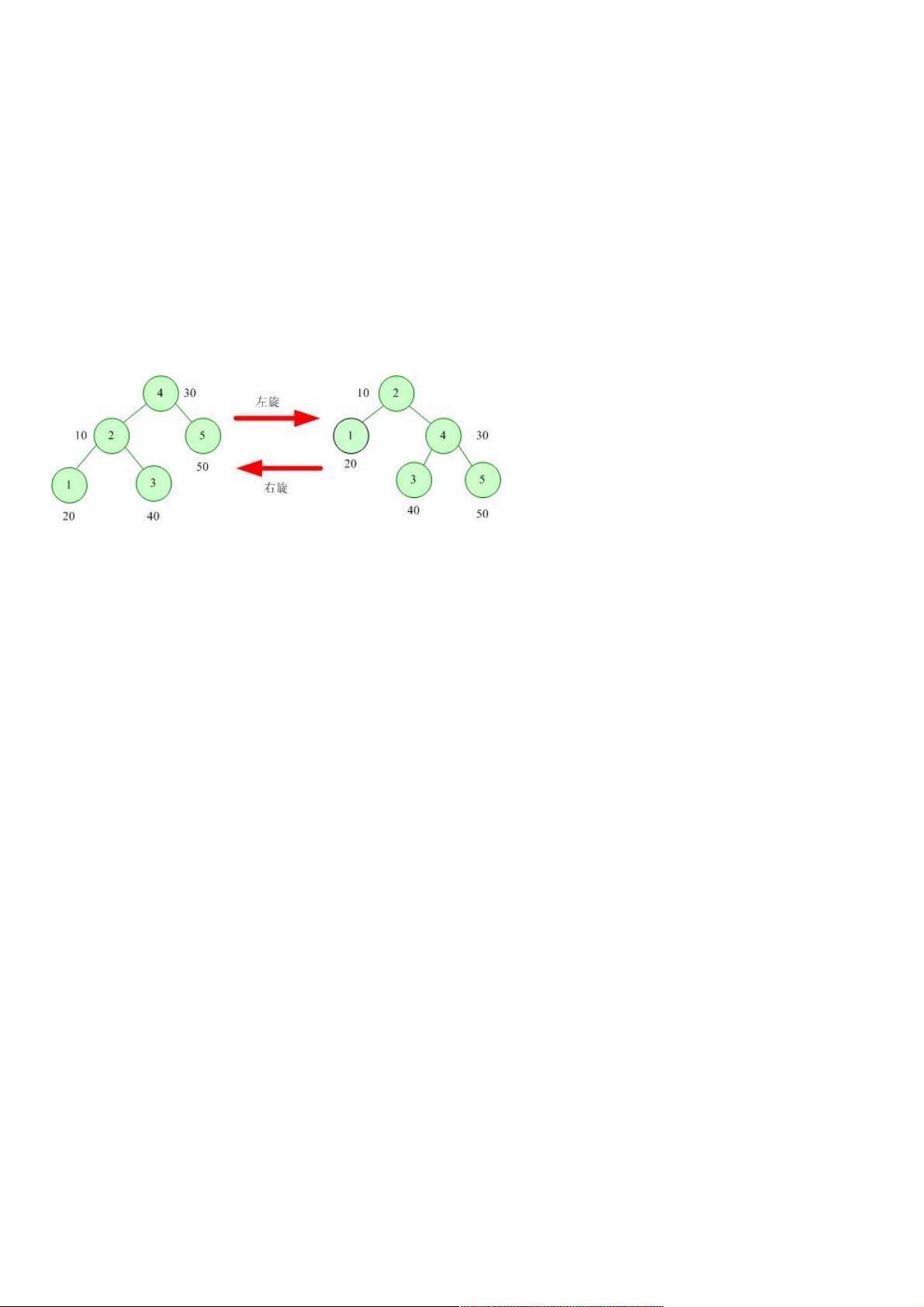
数据结构之Treap详解深入剖析了平衡二叉树的一种特殊变体——Treap（二叉搜索树与堆的结合）。Treap的独特之处在于每个节点除了包含常规的键值对外，还额外记录了一个优先级。这种设计使得Treap同时具备二叉搜索树的有序性和最小堆的特性。 在Treap的基本操作中，核心是旋转操作，用于保持树的平衡和堆的性质。主要有左旋和右旋两种情况：左旋（左旋）将当前节点的右子树提升到其父节点的左侧，而右旋（右旋）则相反，将左子树提升到右侧。这些旋转通过更新节点指针实现，如`Treap_Left_Rotate`和`Treap_Right_Rotate`函数所示，参数为引用是为了避免复制节点。 插入操作在Treap中涉及二分查找找到合适的位置，然后创建新节点并插入。新节点的优先级可能打破原有的堆序，这时就需要通过旋转来调整，确保堆的性质得到维持。插入步骤包括从根节点开始，根据新值与当前节点的比较决定在左子树或右子树中插入，并在必要时进行适当的旋转。 查找操作在Treap中同样遵循二分查找原则，时间复杂度为O(lgn)，这是所有基于二叉搜索树的数据结构共享的特性。删除操作虽然复杂度也为O(lgn)，但需要更细致地处理子树的重新平衡，因为删除可能导致堆序的破坏。 Treap作为一种兼具搜索和排序特性的数据结构，其高效性和灵活性使其在某些场景中具有优势。理解并掌握Treap的旋转操作和基本操作对于实际编程和算法设计至关重要，尤其在需要兼顾搜索性能和堆性质的应用中。