高级数据结构：AVL树与平衡二叉搜索树解析

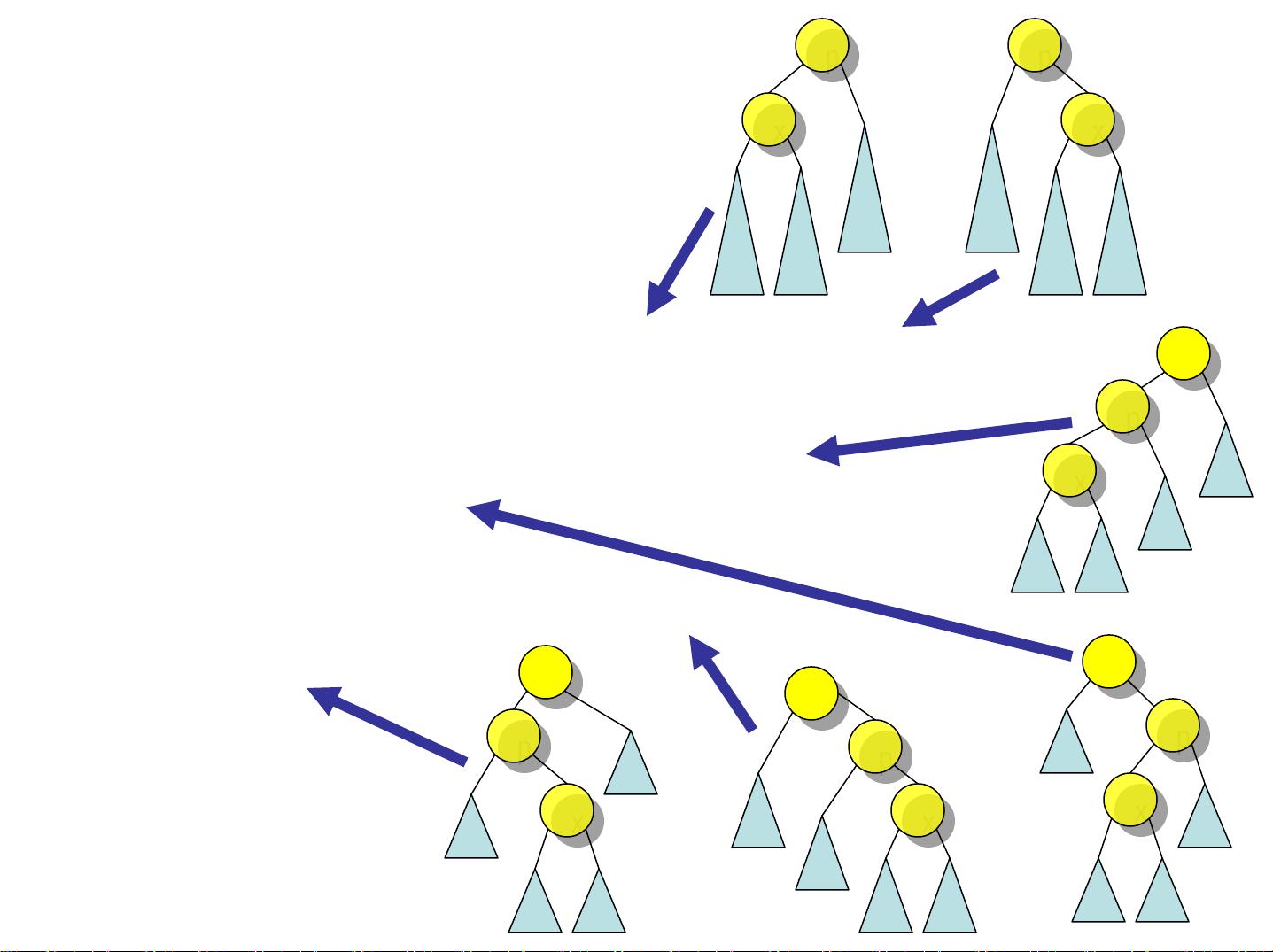
"刘汝佳讲解的高级数据结构课程，主要涵盖了ACM竞赛中常见的高级数据结构，包括平衡二叉树、可并优先队列、线段树和树状数组的基础知识，以及RMQ（Range Minimum Query）和LCA（Lowest Common Ancestor）的应用。" 在计算机科学中，高级数据结构是解决问题的关键工具，尤其是在算法竞赛如ACM中。本课程重点讲解了几个关键的数据结构： 1. 平衡二叉树：基本的二叉搜索树（BST）规定左子树的值小于根节点，右子树的值大于根节点。然而，如果树不平衡，会导致某些操作（如查找、插入和删除）的效率降低。为了保持高效性，我们引入了平衡二叉树的概念，其高度是O(log n)，其中n是节点数量。过于不平衡的树可能导致高度线性，从而严重影响性能。 2. AVL树：AVL树是一种自平衡的二叉搜索树，通过限制任何节点的左右子树高度差不超过1来确保平衡。AVL树的平衡性质保证了查找、插入和删除操作的最坏时间复杂度为O(log n)。当插入或删除导致树不平衡时，通过旋转操作（单旋转和双旋转）恢复平衡。 - 单旋转：分为左旋和右旋，用于解决单边过高的问题。 - 双旋转：当不平衡发生在较远的子节点时，需要进行两次旋转，通常先进行一次单旋转，再进行另一次单旋转。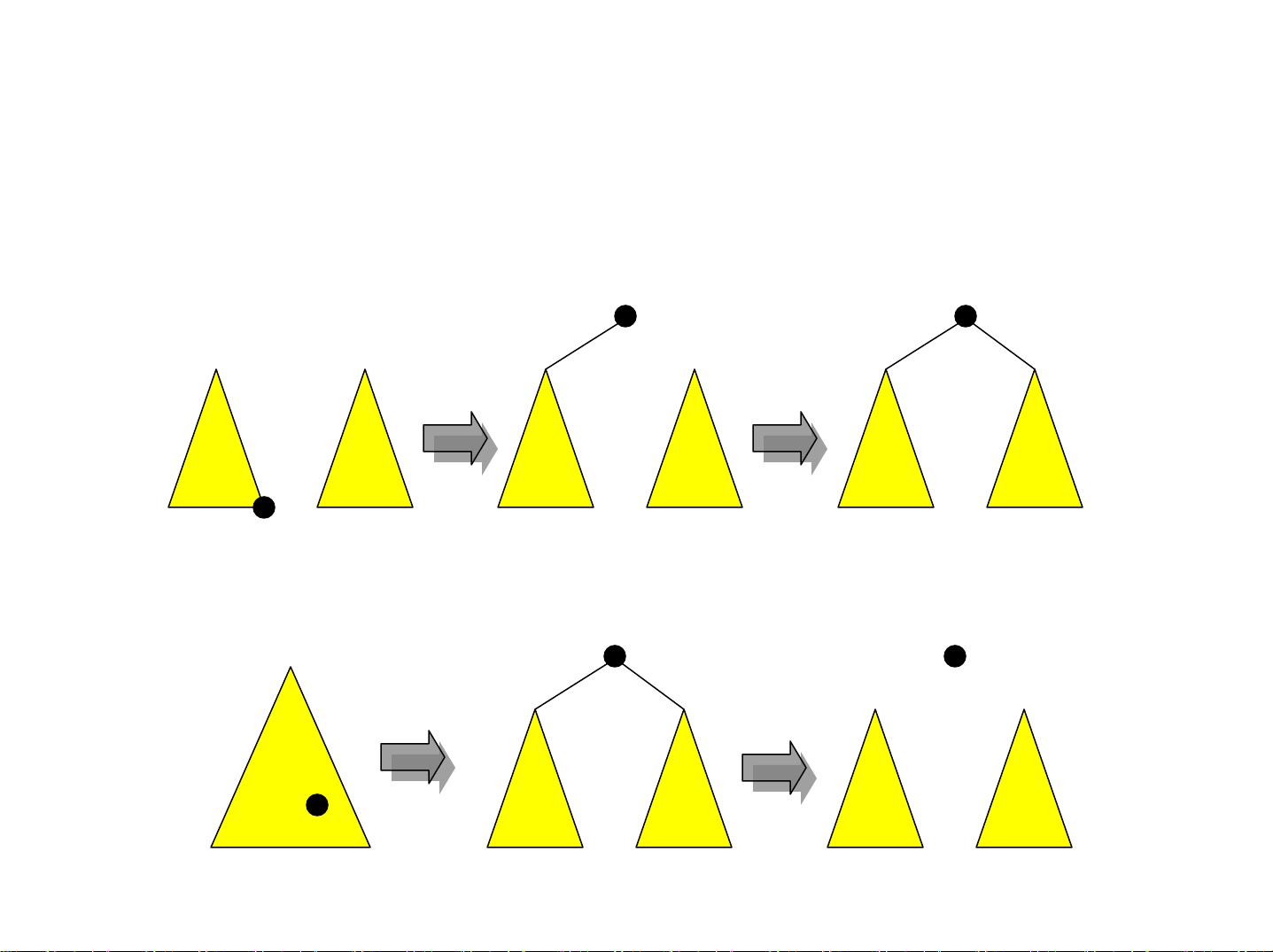 3. 可并优先队列（也称为二项堆或二叉堆）：是一种可以高效合并和操作的优先队列，常用于动态维护最小元素的问题。 4. 线段树和树状数组：这两种数据结构用于高效处理区间查询和区间更新问题。线段树是对数组的一种分治表示，可以快速查询和修改某个区间的所有元素。树状数组（也称为 Fenwick Tree）则使用位操作进行区间查询和更新，具有更低的空间需求。 5. RMQ（Range Minimum Query）：寻找数组（或由其他数据结构表示的序列）中一段连续子序列的最小值。 6. LCA（Lowest Common Ancestor）：在树中找到两个给定节点的最近公共祖先。 学习这些高级数据结构对于提升算法能力和解决复杂问题至关重要，特别是在需要高效处理大量数据和执行复杂操作的场景中。掌握它们将有助于在ACM等算法竞赛中取得优异成绩。