对极几何与三角测量详解：从基础到应用

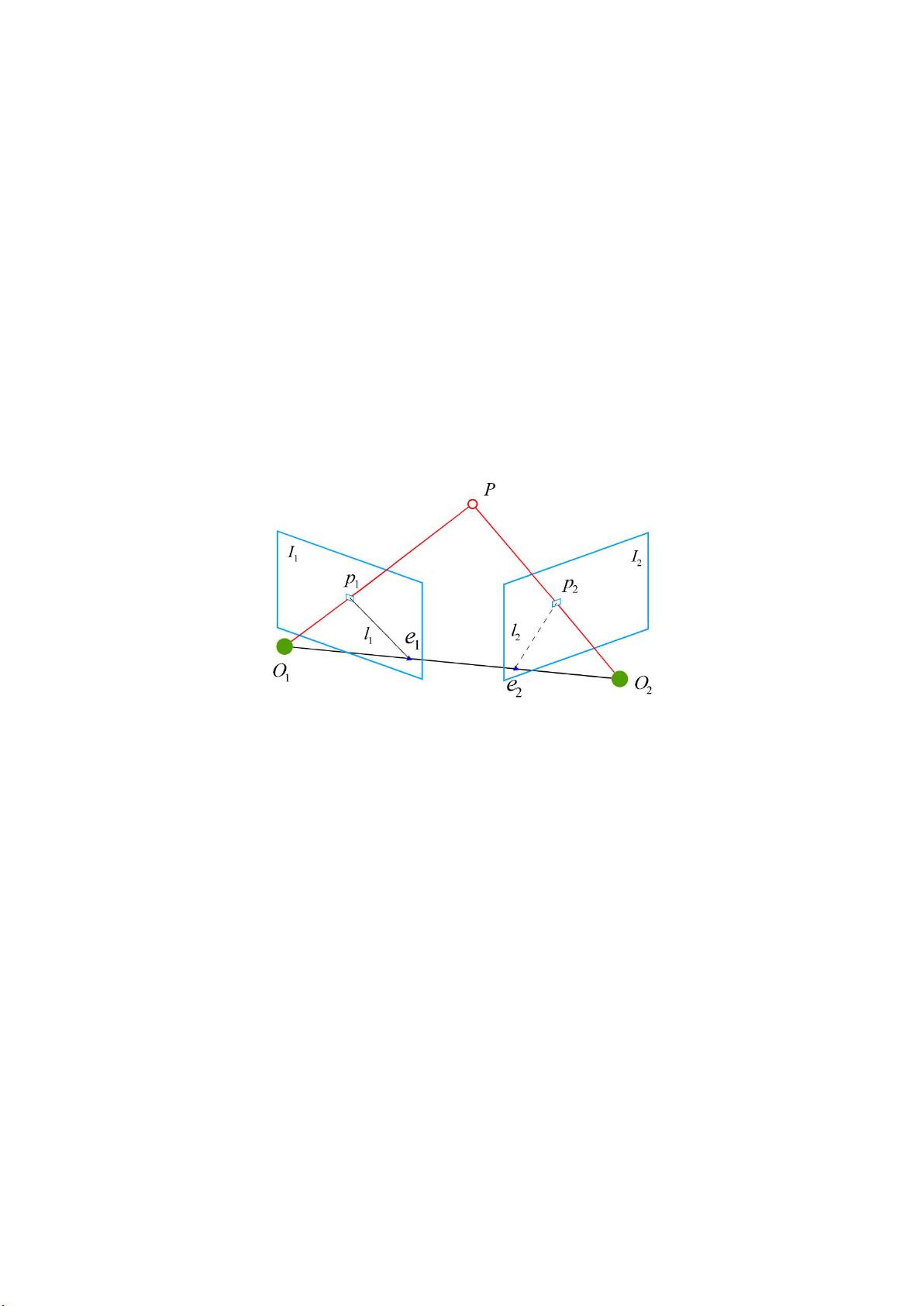
"对极几何与三角测量是计算机视觉领域中的关键概念，它们在多视图几何中扮演着重要角色，特别是在相机定位、立体视觉和SLAM（Simultaneous Localization And Mapping）系统中。对极几何描述了从不同视角观察同一场景时，图像特征之间的约束关系，而三角测量则是通过这些约束恢复3D点的位置。" 一、对极几何的基本思想 对极几何是处理双目或多目视觉系统中图像匹配问题的基础理论。它涉及到两个摄像机的相对位置和姿态，以及它们共同观察的3D点。在对极几何中，存在一个称为极平面的特殊平面，它由3D点、两个相机光心和基线（两相机中心连线）构成。两个相机的成像平面与极平面相交，形成两条极线，每条极线都经过相应的极点（相机光心在对方图像上的投影）。当3D点在第一幅图像上投影为点p1时，其在第二幅图像上的对应点p2必然位于与p1对应的极线上，这一特性极大地简化了特征匹配过程，将二维搜索降为一维搜索。 二、基础矩阵和本征矩阵 基础矩阵(Fundamental Matrix)和本征矩阵(Essential Matrix)是描述两幅图像之间几何关系的数学工具。本征矩阵只包含两相机间的相对旋转和平移信息，是在归一化坐标系下的表示。基础矩阵则更进一步，除了位姿信息外，还包含了相机的内参数，如焦距和主点坐标，它是在图像坐标系中定义的。通过3D点的投影关系，可以推导出这两个矩阵。例如，如果一个3D点P在第一幅图像上的投影为p1，经过相机内参K变换后得到归一化坐标x1，而在第二幅图像上经过旋转R和平移t后的投影为p2，其归一化坐标为x2，那么x2和x1之间的关系可以通过基础矩阵F表示，即x2'Fx1=0。这里的x2'表示x2的转置，遵循矩阵乘法规则。 三、三角测量 三角测量是利用对极几何约束来恢复3D点位置的过程。在已知两幅图像的对应特征点对以及相机的内参和相对姿态后，可以使用三角法计算出3D点的坐标。具体来说，通过两个不同视角的投影方程，可以建立两个线性方程组，然后解这个方程组以找出唯一的3D点。在实践中，由于噪声和匹配误差，通常采用最小二乘法或其他优化算法来估计3D点的精确位置。 总结，对极几何与三角测量是计算机视觉中的核心工具，它们使得在多个视角下重建3D环境成为可能，这对于自动驾驶、机器人导航、虚拟现实等领域的应用至关重要。理解和掌握这些理论，能帮助开发者有效地解决相机定位、立体视觉和SLAM系统中的关键问题。