数据拟合方法：从线性到正交多项式

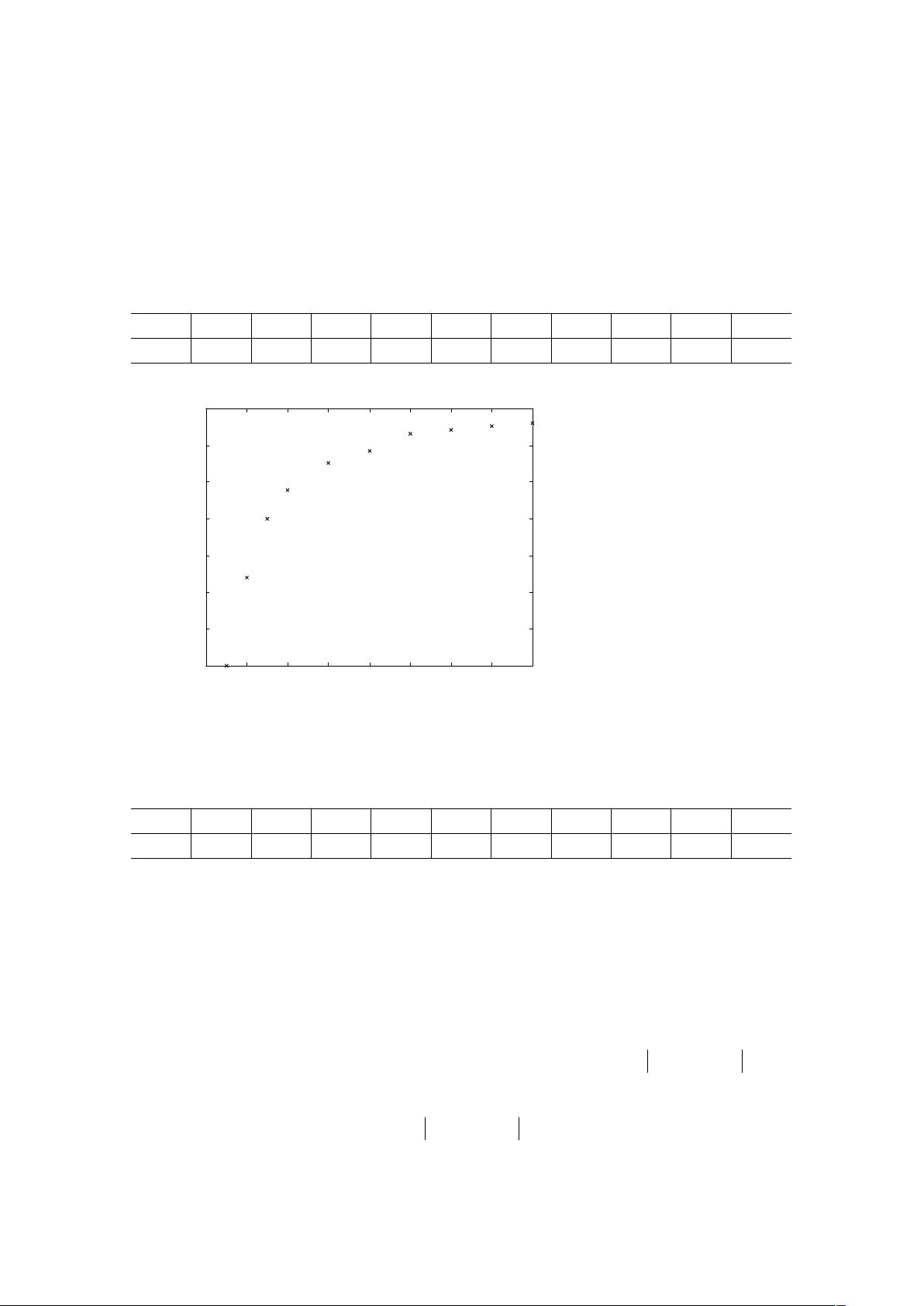
本文档主要探讨了数据拟合的方法，这是在实验科学、社会科学以及行为科学等领域处理大量数据时常用的一种技术。数据拟合的目标是找到一个能够反映数据变化规律的函数，以解释数据或据此做出预测。与数据插值不同，拟合函数不需要通过所有数据点，而是力求贴近数据趋势。 在实际应用中，比如在一个化学反应的例子中，我们可能需要找到质量浓度y与时间t的关系。如果我们假设这个关系可以用一个n次多项式来表示，如 \( y = a_0 + a_1x + a_2x^2 + \ldots + a_nx^n \)，那么我们需要通过数据来确定这个多项式的系数。通常，多项式的阶数n应该小于数据点的数量m。 对于这个n次多项式拟合问题，我们可以建立一个正规方程组来求解，这个方程组的结构是超定的，即方程的数量大于未知数的数量（m > n）。解决这种最小二乘拟合问题相当于找到超定方程组的最小二乘解。然而，由于正规方程组的系数矩阵是病态的，这意味着微小的输入误差可能导致较大的解的误差。为了克服这个问题，可以对多项式进行正交化变换，将原多项式系转换为一组正交多项式系，使得正规方程的系数矩阵变为对角矩阵，从而提高计算的稳定性。 正交多项式系是由点集 \( x_1, x_2, \ldots, x_m \) 上的幂函数通过正交变换得到的，它们满足一定的正交条件。构建正交多项式系的基本步骤包括：首先定义 \( q_0(x) = 1 \)，然后通过迭代过程生成后续的正交多项式 \( q_k(x) \)，每次迭代会使用前两个较低次的正交多项式，并根据特定的系数 \( a_k \) 和 \( b_k \) 更新。 数据拟合是通过选择合适的函数模型来逼近观测数据的过程，正交多项式系提供了一种有效且稳定的手段，尤其在处理高阶多项式拟合和病态方程组时。理解并熟练掌握这些方法对于分析和预测各种复杂数据集的行为至关重要。