USIP：3D点云中的无监督稳定兴趣点检测

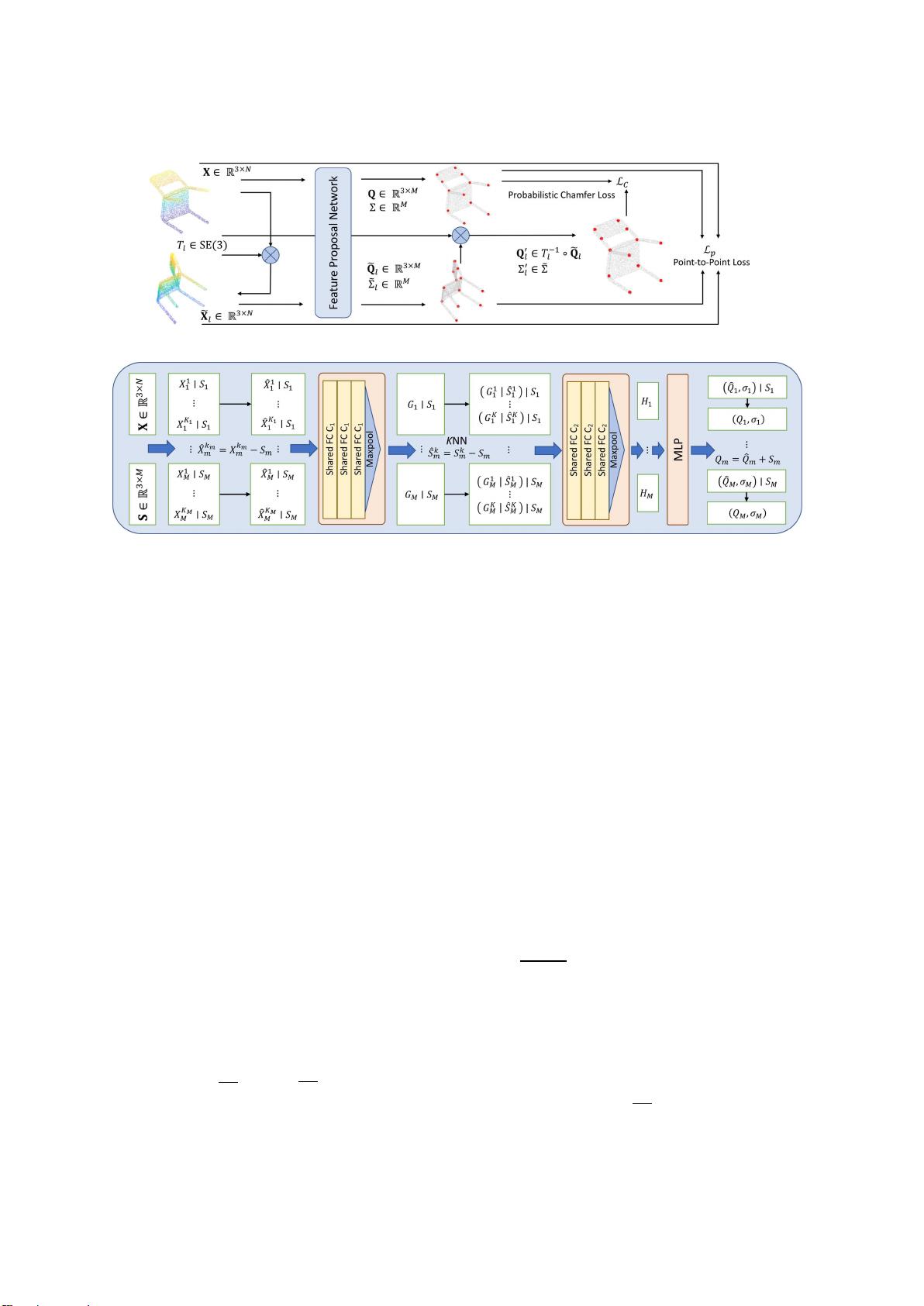
"USIP是无监督稳定兴趣点检测器，专为3D点云设计，能够在各种变换下检测出高度可重复和精确的关键点，无需任何地面实况训练数据。该检测器由特征建议网络构成，通过学习点云的稳定关键点及随机生成的变换对。USIP使用概率倒角损失来提升关键点的可重复性和定位精度。广泛的实验验证了其在模拟和真实3D点云数据集上的优越性能，适用于几何配准、SLAM、3D对象识别等任务。与2D图像的关键点检测相比，3D点云的检测更具挑战性，因为手工制作的检测器较少且效果有限。USIP的代码可在项目网站获取。" 在计算机视觉和机器人领域，3D兴趣点检测是不可或缺的一部分，尤其是在使用3D点云作为数据结构时。USIP检测器解决了这个领域的关键问题，即在SE(3)变换下的稳定性，这对于诸如几何配准、SLAM（Simultaneous Localization and Mapping）和3D对象识别等应用至关重要。USIP通过特征建议网络学习点云中的稳定关键点，同时训练网络适应不同的变换对，以增强关键点的不变性。 为了解决传统手工制作检测器在3D点云处理上的局限性，USIP采取了无监督学习的方法，无需特定环境的标注数据，这意味着它可以应用于各种未见过的场景。通过引入概率倒角损失，USIP确保了检测到的关键点不仅在多个视图之间有高可重复性，而且在定位精度上也有显著提升，这对于保持关键点的匹配一致性至关重要。 在实验部分，USIP在多种数据集上展示了其优秀性能，包括基于激光雷达、RGB-D传感器和CAD模型的点云数据。与现有的手工制作和深度学习的3D关键点检测方法相比，USIP在可重复性和定位准确性上表现出色，表明其在实际应用中的潜力。 此外，USIP的作者还进行了简并性分析，以防止可能影响检测器性能的问题，并提供了相应的解决方案。这一分析确保了USIP在面对各种复杂情况时的稳健性。 USIP是3D点云处理领域的一个突破，为无监督学习的3D关键点检测提供了新的视角。通过克服手工制作检测器的限制，USIP能够处理变换中的3D点云，有望推动计算机视觉和机器人技术的进步。用户可以通过项目网站获取相关的代码，以便在自己的研究或应用中使用。