增强RSA安全性：RBMRSA随机比特填充技术

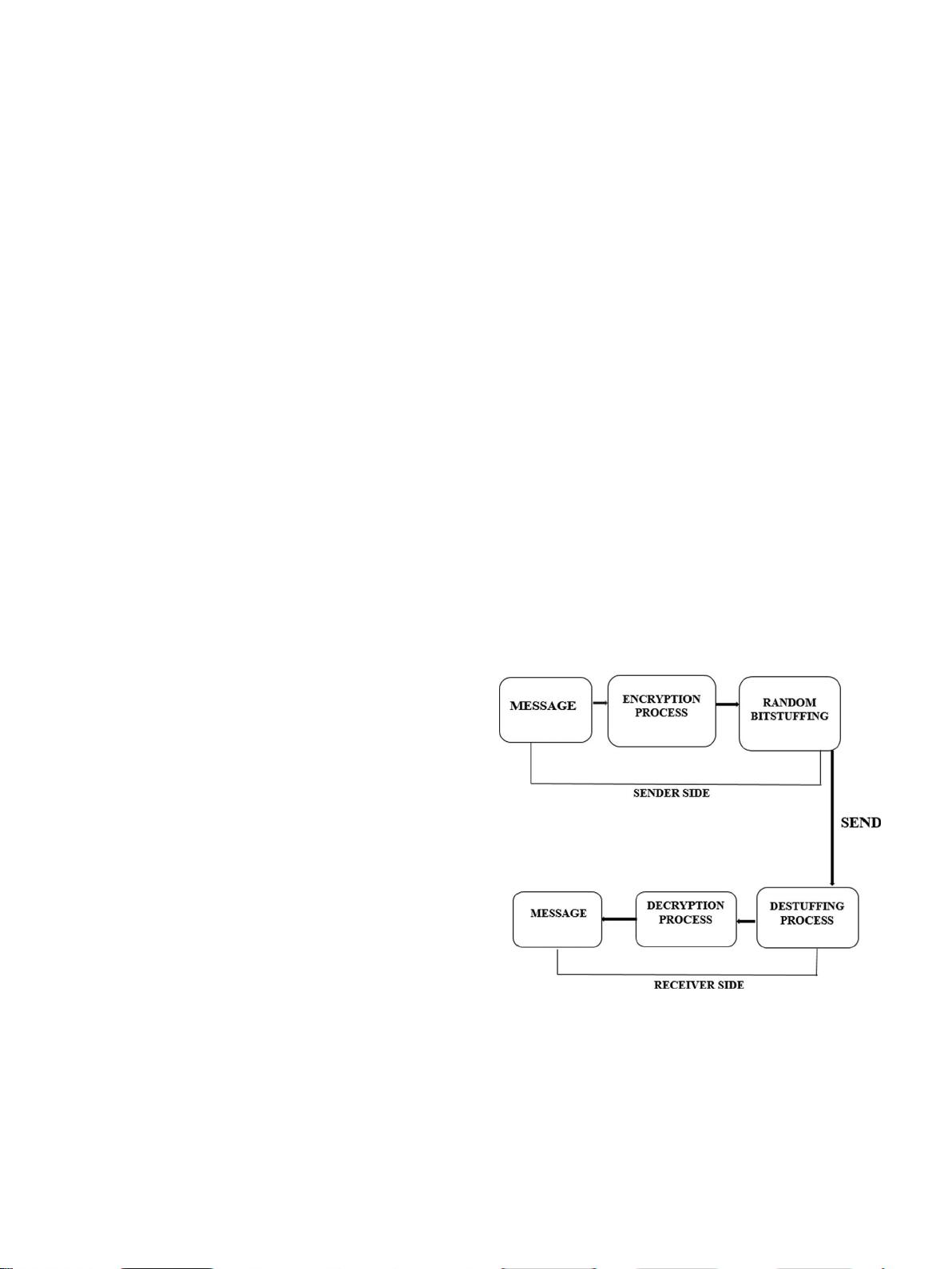
"该文提出了一种改进的RSA算法，名为RBMRSA，旨在提高信息安全性和防御各种攻击。研究者通过增强位插入算法提升了RSA的加密安全性，同时保持了1024密钥长度，避免了密钥扩展。RBMRSA在安全性上表现出优于传统RSA的性能，尽管在执行时间上可能有所增加。文章通过数学评估和实验对比，使用雪崩效应和计算复杂度作为衡量标准，验证了其改进的有效性。" 在信息安全领域，RSA算法是一种广泛应用的公钥加密技术，由Ron Rivest、Adi Shamir和Leonard Adleman于1977年提出。它基于大整数因子分解的困难性，为数据提供了机密性和完整性保障。然而，随着计算机技术的进步，传统RSA算法的密钥长度逐渐显得不足，容易受到如穷举搜索攻击等威胁。 RBMRSA是针对这一问题的解决方案，它在RSA基础上引入了随机比特填充技术，增强了加密过程中的随机性，以提高对不同攻击的抵抗力。随机比特插入算法可以增加密文的混淆程度，使得攻击者更难以通过分析模式找出加密规则，从而提高了安全性。这种改进还旨在增加数据的扩散性，即使不增加密钥长度，也能让加密后的数据更加难以破解。 文章中提到的雪崩效应是指输入的微小变化导致输出的巨大变化，这是衡量加密算法强度的重要指标。如果一个加密算法具有良好的雪崩效应，那么任何输入的微小变化都会在整个输出中产生不可预测的变化，这使得攻击者更难以通过分析部分信息推断出全部信息。 此外，计算复杂度是评估加密算法性能的另一个关键因素，它涉及到算法运行所需的时间和资源。虽然RBMRSA在安全性上有所提升，但可能会带来更高的计算复杂度，这意味着加密和解密过程可能需要更长的时间。然而，考虑到安全性的提升，这种牺牲可能是值得的。 RBMRSA提供了一种改进的加密方法，能够在不显著增加计算负担的情况下，提高数据加密的安全性，尤其对抗网络攻击。这对于依赖网络进行敏感信息交换的企业和个人来说，具有重要的实际意义。