NI-Louvain: 社交网络中的影响力驱动社区检测算法

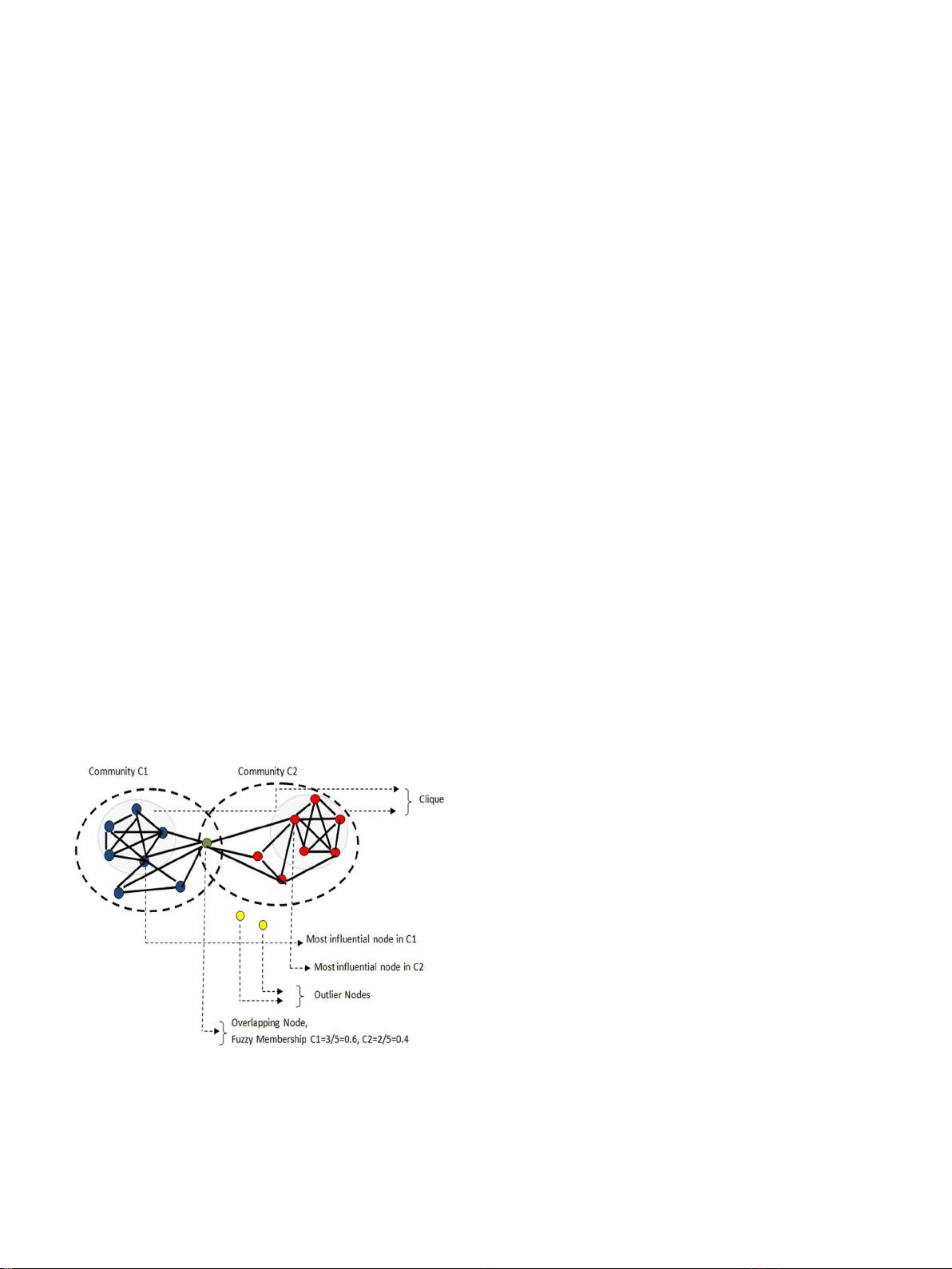
"NI-Louvain：基于影响分析的社区检测算法研究"是一篇发表在沙特国王大学学报的计算机科学研究论文，主要探讨了社区发现这一在社交媒体挖掘领域中至关重要的课题。传统算法往往忽视了网络中每个节点对社区结构的影响，而这对于准确识别社区特性至关重要。作者Dipika Singha和Rakhi Garg针对这一问题提出了一个新的算法——NI-Louvain。 NI-Louvain算法的核心在于它考虑了每个节点在群体中的影响力，不仅聚焦于社区划分，还试图确定每个社区内的主导节点。算法分为三个步骤：首先，通过降低图的密度来简化处理，通过集团划分来实现；接着，采用Louvain的多级算法对简化后的图进行社区检测，这种方法在模块化值上表现出色，超越了诸如边缘介数、标签传播、领先特征、Louvain、快速贪婪、walktrap和信息地图等现有算法。 在第三步，算法将处理后的结果社区映射回原始图的节点，这样可以更好地识别重叠社区、每个节点模糊的社区归属，以及每个社区内的最具影响力节点，甚至能检测到离群节点。这种对节点影响力的关注使得NI-Louvain在复杂社交网络中展现了更强的适应性和准确性。 文章的背景指出，随着互联网的普及和社交网络的盛行，社区检测技术的应用范围广泛，如推荐系统、用户行为分析等。然而，NI-Louvain的独特贡献在于其对节点影响力因素的整合，这无疑提升了社区检测的精确性和有效性。 该研究论文于2021年发布，并遵循了Creative Commons Attribution-NonCommercial-NoDerivatives (CC BY-NC-ND) 4.0许可协议，这意味着读者可以自由地访问和分享文章，但不允许商业使用或修改内容。整体而言，NI-Louvain算法是一项创新的工作，对理解社交网络中的社区结构和节点角色具有重要意义。"