ARAPReg：参数化形状生成器的无监督学习方法

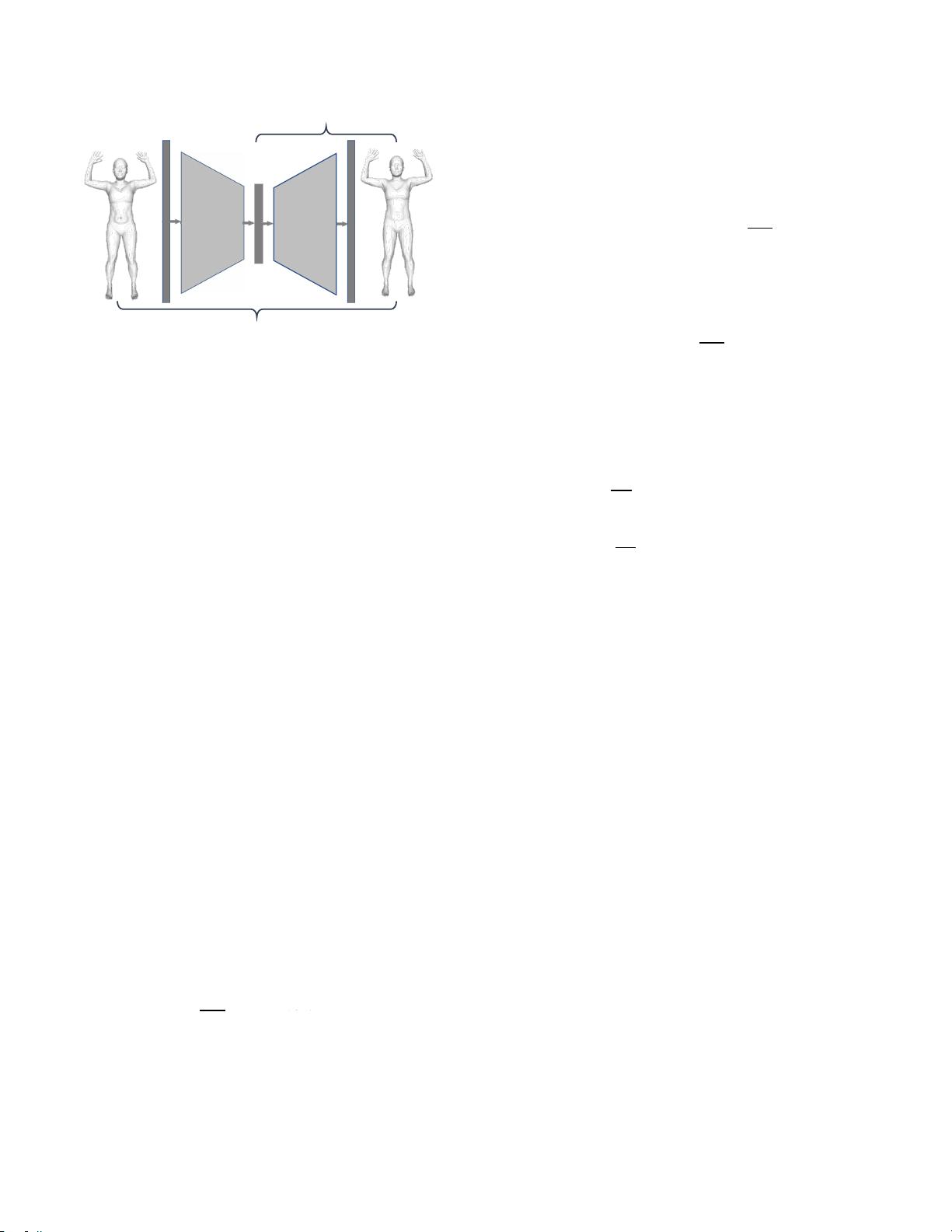
ARAPReg是一种创新的无监督学习方法，旨在从可变形形状的集合中训练形状生成器，特别关注于保持形状的局部刚性。这种方法由UT奥斯汀的研究团队提出，包括黄启星、张在伟、Xiangru Huang、江俊峰、Bo Sun、Chandrajit Bajaj等专家。传统上，形状生成器往往面临如何捕捉并保持形状变化中的关键结构难题，比如人脸的特征或动物的脚趾位置。 ARAPReg的核心在于其独特的无监督损失函数，该损失基于ARAP（Approximate Rigidity and AreaPreserving）能量的Hessian谱分解。ARAP能量模型强调形状之间的局部刚性保持，确保生成的新形状在相邻部分之间的变形尽可能接近刚体运动。这种损失设计巧妙地分离了形状变化与姿势变化，提供了更清晰的表示，并允许通过标准模型如变分自编码器（VAE）和自动解码器（AD）进行有效训练。 与现有形状生成方法相比，ARAPReg的优势在于其对各种形状类别的适应性，如人类、动物和骨骼，尤其是在处理大规模几何变化时表现出色。这种方法不仅能够复现复杂的形状变换，而且能够保持生成形状的自然约束，这对于视觉计算任务如神经形态发生恢复、数据驱动的形状重建以及基于图像的重建等领域具有重要意义。 通过实验验证，ARAPReg在公共基准数据集上的性能显著优于同类技术，证明了其在形状生成领域的有效性。研究者提供的代码和数据可在GitHub上获取，以便研究人员进一步探索和应用这一创新的无监督学习策略。