深度学习方向感知特征：非刚性形状匹配的新突破

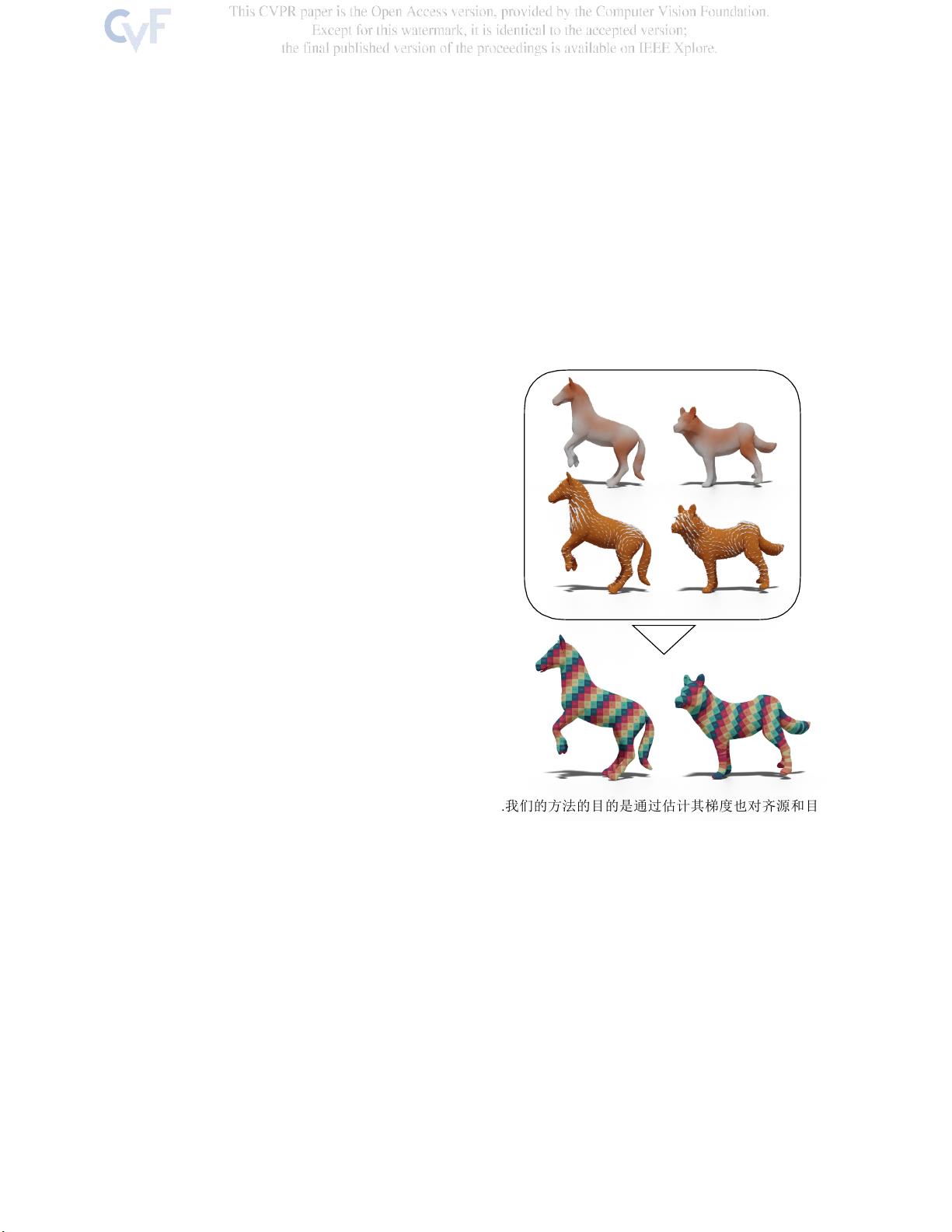
深度方向感知功能地图（DUO-FM）是一种创新的深度学习方法，针对非刚性形状匹配问题提供了一种解决方案。传统的全内在网络在处理形状内部对称性时存在歧义，而功能图框架通过复杂功能图实现了方向保持，使用向量场转移的功能表示来强制保持形状的方向一致性。DUO-FM的核心在于结合了DiffusionNet架构，这是一种对离散化变化具有鲁棒性的模型，同时引入了基于矢量场的损失，无需依赖外部不稳定描述符，能够实现无监督下的方向感知特征学习。 该方法首先回顾了非刚性形状对应学习的重要性，它在3D形状分析中扮演着关键角色，包括统计形状分析和变形纹理转移等领域。早期的方法主要侧重于特征描述符的学习，如[26]，或者通过预测每个点的对应顶点ID，如[28, 31, 37, 51]。然而，这些方法缺乏一致性，并可能受到形状离散化的敏感性影响。 近期的技术发展聚焦于整体地图谱预测，特别是函数映射表示，它们利用谱特征将映射转换为小矩阵，显著推动了这一领域的发展。关键在于学习特征函数并应用于整体预测，这种方法降低了对监督数据的需求，提供更强的正则化，使特征对离散化变化更为稳健，并且在存在固定模板形状的情况下简化了预测过程。 DUO-FM的独特之处在于其完全无监督的学习环境，通过估计描述符的梯度，确保源和目标形状在功能上保持一致。这种设计不仅提高了匹配的精度，而且减少了对大量标注数据的依赖，对于实际应用具有显著优势。此外，该方法的源代码已公开在GitHub上，方便研究人员和开发者进行进一步的研究和实践。 总结来说，深度方向感知功能地图为解决非刚性形状匹配问题提供了一个强大的工具，通过结合方向感知、鲁棒的离散化处理和无监督学习，为3D形状分析领域的研究者和实践者带来了突破性的进展。