并行最优传输GAN算法：提升GAN训练效果与模式多样性

"并行最优传输GAN算法是针对生成对抗网络（GAN）训练质量和模式覆盖问题的一种新方法，由吉尔·亚伯拉罕、严佐汤和姆·德拉蒙德提出。该算法在低维表示空间内并行执行最优传输，以改善GAN训练的稳定性和生成样本的质量，增加数据分布的模式覆盖。研究表明，这种方法在CIFAR-10、OxfordFlowers和CUBBirds数据集上实现了显著的定性和定量提升。" 生成对抗网络（GANs）是一种强大的生成模型，由两个相互竞争的网络组成：生成器（Generator）和鉴别器（Discriminator）。生成器尝试从随机噪声中生成逼真的样本，而鉴别器试图区分真实数据与生成的样本。然而，GANs在训练过程中存在一些固有问题，如低模态多样性和样本失真，这些问题主要源于距离度量的不准确估计。 最优传输（Optimal Transport）理论在统计学和机器学习中有广泛应用，其在解决大规模问题时表现出良好的直观性和数值稳定性。在GANs中，最优传输被用来估计Wasserstein距离，有助于缓解训练不稳定性，如消失梯度和模式崩溃。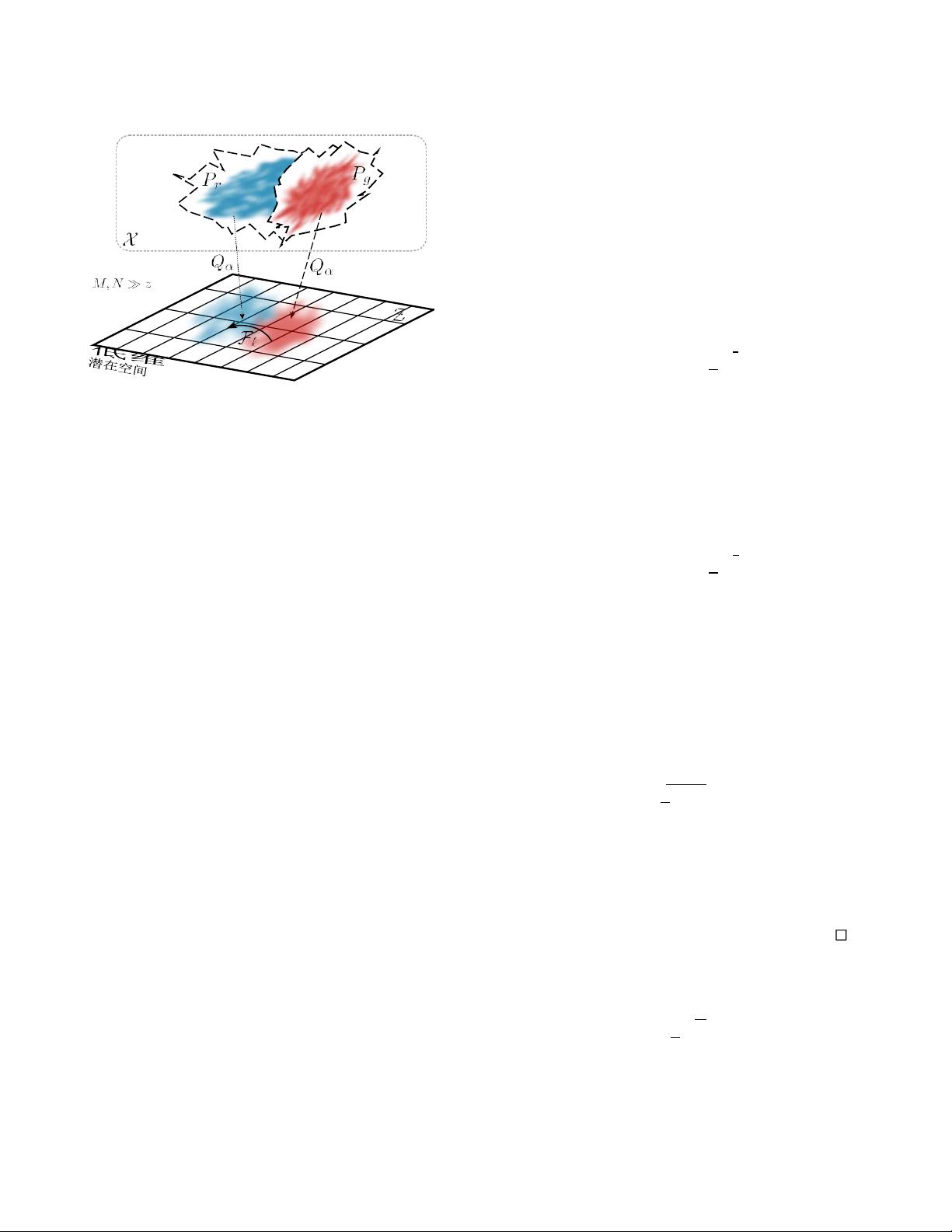 论文中提出的并行最优传输GAN算法引入了一个新的正则化项，这个项在数据分布的低维表示空间中并行执行，以加速Wasserstein距离的估计收敛速度。通过这种方式，算法能够提供更稳定的训练过程，生成更高质量的样本，并增加对原始数据分布的模式覆盖。 实验结果表明，这种方法在多个数据集上的表现优于传统GAN训练，包括在CIFAR-10（一个常用的彩色图像数据集）、OxfordFlowers（花卉识别数据集）和CUBBirds（鸟类识别数据集）上，不仅提高了生成样本的视觉质量，还量化地提升了模式多样性。 这一并行最优传输GAN算法为解决GAN训练中的挑战提供了新的视角，通过优化距离度量的估计，提高了生成模型的性能，有望在图像生成和其他应用领域带来更优秀的成果。