光场盲运动去模糊：理论与算法突破

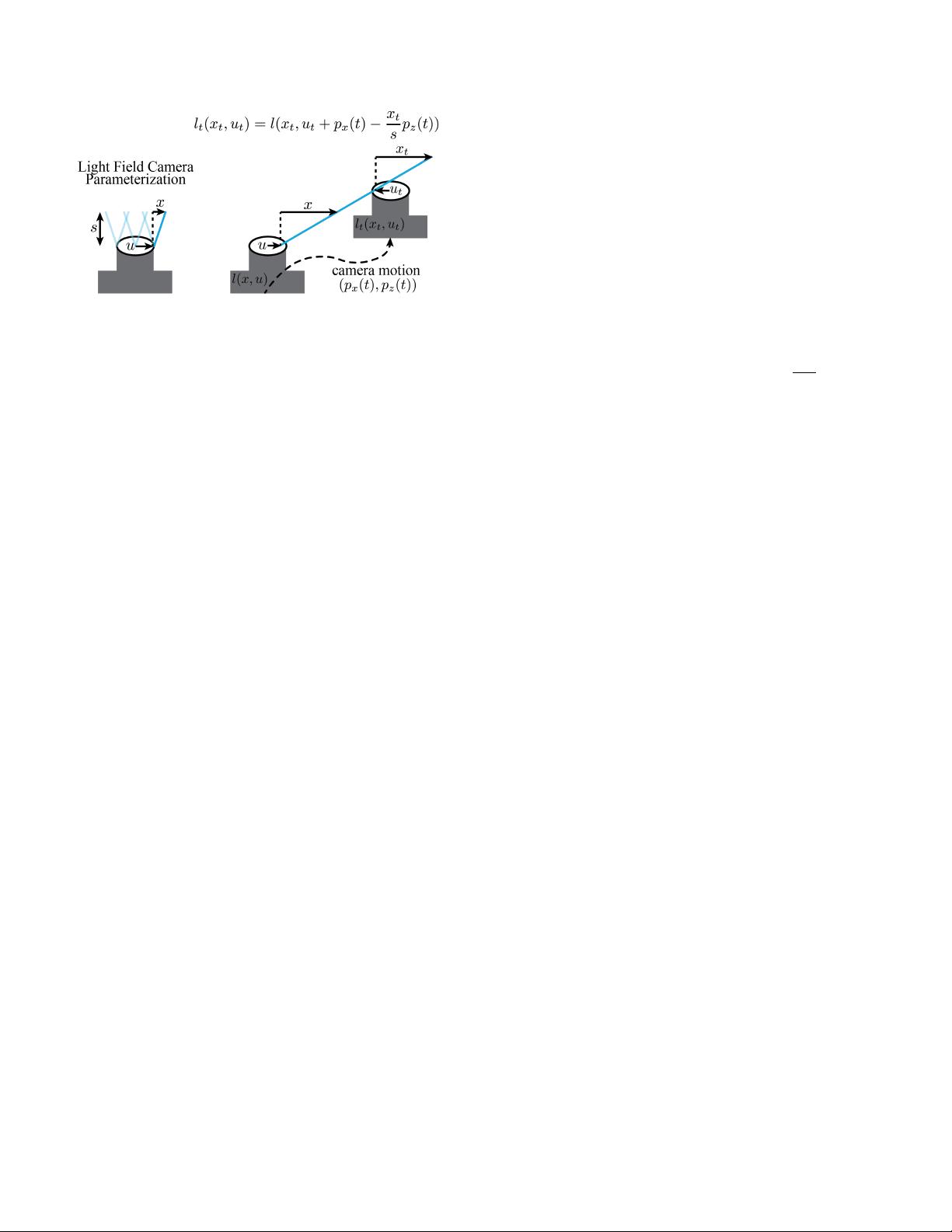
光场盲运动去模糊方法的研究 本研究论文探讨了在三维摄像机运动的光场中去除运动模糊的问题，其主要背景是运动模糊是由物体和摄像机之间的相对运动导致的，尤其是在光场相机中，由于场景深度范围广泛和相机的平面外运动，运动模糊的影响尤为显著。作者普拉图尔山口Srinivasan和Ren Ng，以及Ravi Ramamoorthi来自加州大学伯克利分校和圣地亚哥分校，他们的研究专注于理解运动模糊对光场的影响，并提出了一种创新的处理策略。 论文首先介绍了运动模糊的普遍性，指出传统的二维图像处理无法完全捕捉到这种现象的复杂性。他们观察到，对于平移运动，光场模糊可以简化为清晰光场与摄像机运动路径内核的卷积，这一特性使得在光场中应用简单的去卷积技术成为可能，从而恢复出清晰的图像，这是传统图像处理中不具备的能力，因为运动模糊的程度会随深度变化（如图1A和1B所示）。 对于更复杂的平面外运动，他们理论推导了一个前向模型，表示运动模糊光场是沿相机运动路径的尖锐光场经过积分变换的结果。通过分析原始域和傅立叶域中的运动模糊光场，他们发现捕捉到的4D光场提供了关键信息，有助于区分传统二维图像无法提供的运动模糊特征。在不依赖于精确场景几何形状的情况下，他们提出了一种盲运动去模糊算法，能够在不知晓合成运动路径的情况下，准确地恢复出光场的清晰度和相机的运动轨迹（如图9所示的实际手持摄像机运动案例）。 这项工作不仅提升了对运动模糊现象的理解，还提供了一种实用的工具，特别是在光场相机的应用中，如增强现实、虚拟现实和三维重建等领域。它扩展了运动去模糊技术的传统边界，使得在处理动态场景时能更有效地恢复细节和清晰度。