首页
矩阵A,B满足AX= B,X是啥矩阵
矩阵A,B满足AX= B,X是啥矩阵
时间: 2024-02-03 11:02:03
浏览: 162
如果矩阵 $A$ 和 $B$ 满足 $AX=B$,那么 $X$ 矩阵应该是 $A$ 的逆矩阵与 $B$ 的乘积,即 $X=A^{-1}B$。其中,$A$ 的逆矩阵存在的前提是 $A$ 是一个可逆矩阵,也就是说 $A$ 的行列式不为零。如果 $A$ 不可逆,则方程组 $AX=B$ 可能无解或者有无限解。
阅读全文
相关推荐
AXI矩阵
AXI矩阵
矩阵方程AX=B的实部正定解 (1998年)
首先,对于矩阵方程AX=B,其中A、B属于复数域上的矩阵,研究者们关注的是当存在解时,解矩阵X的实部是否能够保持正定。这里需要明确何为实部正定矩阵。若对于所有非零复向量x,矩阵A的实部H(A)与x的点积大于零,即Re...
使用增广矩阵求解Ax=B
当我们遇到一组线性方程,如Ax=B,其中A是一个系数矩阵,x是未知数向量,而B是常数项向量时,使用增广矩阵是一种有效的方法来找到解决方案。在给定的标题"使用增广矩阵求解Ax=B"中,我们关注的是如何通过...
一类矩阵方程组AX=B,XD=E的对称解与反对称解 (2015年)
考虑矩阵方程组AX=B,XD=E的对称解与反对称解,利用对称(反对称)矩阵的性质和矩阵对的标准相关分解(CCD),给出了矩阵方程组对称解(反对称解)存在的充分必要条件及解的一般表达式,并讨论了对任意给定矩阵的最佳逼近问题.
矩阵方程AX=B,XC=D的(M,N)-反对称解 (2016年)
这里,通解意味着所有满足方程AX=B,XC=D的(M,N)-反对称矩阵X的集合。而解的表达式则提供了一个普遍形式,使得对于任意给定的A和C矩阵,都可以构造出一个对应的(M,N)-反对称解X。 此外,研究还考虑了最佳逼近问题。...
求上三角系数矩阵的线性方程组Ax=b的解
求上三角系数矩阵的线性方程组Ax=b的解,数值计算,求解方程
求解矩阵方程AX=B的多步迭代算法.docx
该算法的收敛性定理是:若矩阵A为列满秩矩阵,则由算法1产生的矩阵序列{Xk}收敛于矩阵方程AX=B在Rn×n内的唯一解X*=A+B;若矩阵A为非列满秩矩阵,则由算法1产生的矩阵序列{Xk}收敛于矩阵方程AX=B在Rn×n内的最小 ...
矩阵方程AX=B的广义Hermite解及最佳逼近问题
矩阵方程AX=B的广义Hermite解及最佳逼近问题,梁茂林,,本文给出广义酉矩阵和广义Hermite矩阵的定义,通过奇异值分解讨论了其性质;对给定矩阵X,B,得到了矩阵方程AX=B有广义Hermite解的充要条�
用C语言求解N阶线性矩阵方程Ax=b的简单解法
double a[dim+1][dim+1], b[dim+1], x[dim+1]分别用于存储系数矩阵A、常数向量b和未知向量x。temp作为临时变量用于交换或计算。 2. **输入矩阵元素**: getarray(int n)函数用于从用户处获取n阶系数矩阵...
jacobi(A,b):用JACOBI数值方法计算矩阵Ax = B的结果的代码-matlab开发
在本文中,我们将深入探讨如何使用MATLAB编程语言实现雅可比迭代法(Jacobi Iteration)来解决线性方程组Ax = B的问题。雅可比方法是一种经典的数值求解技术,尤其适用于大型稀疏矩阵。让我们首先理解雅可比方法的...
用C语言求解N阶线性矩阵方程Ax=b的简单解法.docx
这里的A是一个N×N的矩阵,x是待求解的未知数向量,b是一个已知的N维向量。在数学中,这种类型的方程组很常见,并且有多种方法可以解决这类问题。本文将重点介绍如何使用C语言实现高斯消元法来求解该方程组。 #### ...
分辨率 Ax=B:求解线性系统 Ax=B 的程序-matlab开发
对于Ax=B的系统,我们可以使用inv(A)*B来找到x的值。然而,直接计算逆矩阵可能会导致数值不稳定,特别是当矩阵接近奇异时,因此在实际应用中应谨慎使用。 接下来,辅因子(或余子矩阵的行列式)是计算矩阵秩和...
一类线性流形上矩阵方程AX = B的反问题 (2009年)
本文的标题《一类线性流形上矩阵方程AX = B的反问题》和描述指出文章将探讨在特定线性流形上,给定X和B时,求解满足方程AX = B的矩阵A的问题,以及给定A*时,寻找在特定解集合SE中逼近A*的矩阵^A的问题。 文章的...
矩阵方程AX=B的中心对称解及其最佳逼近* (2007年)
基于一种新的思路,本文将一类约束矩阵方程问题化为无约束矩阵方程问题,从而轻易地获得了简洁且满意的结果.
Jacobi:使用Jacobi方法的序列化和并行化形式求解矩阵方程Ax = B
该项目使用Jacobi算法的顺序和并行版本处理矩阵方程Ax = B。 Jacobi算法的并行化形式使用Java的Fork / Join将问题递归分解为由许多线程并行解决的较小部分。 这两种测试器方法可用于直接在控制台上测试简单的小尺寸...
矩阵方程AX=B的正交(P, Q)-对称解 (2014年)
定义了正交(P, Q)-对称矩阵的概念,通过矩阵的正交投影构造了它的结构,针对正交(P, Q)-对称矩阵的正交不变性,采用直接代入法把问题转化为...最后得出矩阵方程AX=B有正交(P, Q)-对称解的充要条件及通解表达式。
Efficient Successive Over-Relaxation Method:此代码使用带状 SOR 求解线性系统 Ax=b,其中 A 是对称带状矩阵。-matlab开发
目标:此代码求解线性系统 Ax=b,其中 A 是对称带状矩阵,使用带状 SOR。 A首先以compact存储方式存储和下一个 SOR 应用于紧凑存储。 输入:此代码接受对称带状矩阵 A,初始猜测 x0, 向量 b,SOR 参数 omega 和容差...
MATLAB高斯消去法、LU分解法求Ax=b,求逆矩阵
在MATLAB环境中,高斯消去法和LU分解法是解决线性代数方程组Ax=b的重要工具,同时也常用于求解矩阵的逆和计算行列式。这两种方法都基于矩阵的运算,但LU分解法提供了更为高效和灵活的解决方案。 高斯消去法是一种...
代数多重网格线性求解器:该程序求解 Ax=b,其中 A 是 M 矩阵。 可以在 AMG_test.m 找到测试用例-matlab开发
该程序基于86中Ruge和Stuben的算法实现。有一组参数可供用户根据自己的应用进行调整,包括连接阈值、松弛参数、平滑器类型和平滑步数等。欢迎用户使用修改此代码。 但是,作者根本不作任何保证。...
CSDN会员
开通CSDN年卡参与万元壕礼抽奖
海量
VIP免费资源
千本
正版电子书
商城
会员专享价
千门
课程&专栏
全年可省5,000元
立即开通
全年可省5,000元
立即开通
大家在看
chessClock:一个简单的Arduino Chess Clock,带有3个按钮和LCD 240X320屏幕
弗洛伊斯国际象棋时钟 一个带有3个按钮和240X320 LCD屏幕的简单Arduino国际象棋时钟 这是隔离期间开发的一个简单的棋钟项目。主要灵感来自@naldin的 。我更改了他的代码,所以我只能使用三个按钮(暂停,黑白)来选择国际象棋比赛中最常用的时间设置,并在LCD屏幕上显示小时数。该项目目前处于停滞状态,因为我使用的Arduino Nano已损坏,我找不到新的。尽管项目运行正常,但您只需要正确地将LCD屏幕连接到相应的SPI引脚,并将按钮连接到所需的任何数字引脚即可。另外,我仍然需要在时钟上打印3D框或找到一个3D框使其播放。很快,我将更新此页面。
学堂云《信息检索与科技写作》单元测试考核答案
学堂云《信息检索与科技写作》单元测试考核答案 【对应博文见链接:】https://blog.csdn.net/m0_61712829/article/details/135173767?csdn_share_tail=%7B%22type%22%3A%22blog%22%2C%22rType%22%3A%22article%22%2C%22rId%22%3A%22135173767%22%2C%22source%22%3A%22m0_61712829%22%7D
【蒙特卡洛模拟】这个项目旨在通过强化学习和蒙特卡洛模拟的结合,解决银行购买股票的最优策略和预期利润折现率的问题KL.zip
【蒙特卡洛模拟】这个项目旨在通过强化学习和蒙特卡洛模拟的结合,解决银行购买股票的最优策略和预期利润折现率的问题【KL】.zip
码垛机器人说明书
对于随机货盘来说,码垛机器人是唯一的选择。尽管如此,机器人装载也面临比较多的问题,如果要以较高的速度进行生产,将更加困难重重。一个处理随机装载的机器人码垛机需要特殊的软件,通过软件,机器人码垛机与生产线的其他部分相连接,这是个巨大的进步。
《智能调度集中系统暂行技术条件》.pdf
智能调度
最新推荐
用C语言求解N阶线性矩阵方程Ax=b的简单解法
`double a[dim+1][dim+1]`, `b[dim+1]`, `x[dim+1]`分别用于存储系数矩阵A、常数向量b和未知向量x。`temp`作为临时变量用于交换或计算。 2. **输入矩阵元素**: `getarray(int n)`函数用于从用户处获取n阶系数矩阵...
C++ Eigen库计算矩阵特征值及特征向量
特征向量是满足 Ax = λx 的非零向量x。 使用Eigen库计算矩阵特征值和特征向量 Eigen库提供了一个名为EigenSolver的类,用于计算矩阵的特征值和特征向量。下面是一个简单的示例代码: ```cpp #include #include ...
矩阵求导包括矩阵对矩阵求导.docx
这是因为X^TA的偏导数关于X是A,而AX的偏导数关于X是AT。所以总导数是这两个部分的和,因为它们是独立的。 接下来,我们转向“矩阵对矩阵求导”,也称为弗雷德霍姆导数或弗雷德霍姆积分算子。在这个情况下,我们有...
免安装JDK 1.8.0_241:即刻配置环境运行
资源摘要信息:"JDK 1.8.0_241 是Java开发工具包(Java Development Kit)的版本号,代表了Java软件开发环境的一个特定发布。它由甲骨文公司(Oracle Corporation)维护,是Java SE(Java Platform, Standard Edition)的一部分,主要用于开发和部署桌面、服务器以及嵌入式环境中的Java应用程序。本版本是JDK 1.8的更新版本,其中的241代表在该版本系列中的具体更新编号。此版本附带了Java源码,方便开发者查看和学习Java内部实现机制。由于是免安装版本,因此不需要复杂的安装过程,解压缩即可使用。用户配置好环境变量之后,即可以开始运行和开发Java程序。" 知识点详细说明: 1. JDK(Java Development Kit):JDK是进行Java编程和开发时所必需的一组工具集合。它包含了Java运行时环境(JRE)、编译器(javac)、调试器以及其他工具,如Java文档生成器(javadoc)和打包工具(jar)。JDK允许开发者创建Java应用程序、小程序以及可以部署在任何平台上的Java组件。 2. Java SE(Java Platform, Standard Edition):Java SE是Java平台的标准版本,它定义了Java编程语言的核心功能和库。Java SE是构建Java EE(企业版)和Java ME(微型版)的基础。Java SE提供了多种Java类库和API,包括集合框架、Java虚拟机(JVM)、网络编程、多线程、IO、数据库连接(JDBC)等。 3. 免安装版:通常情况下,JDK需要进行安装才能使用。但免安装版JDK仅需要解压缩到磁盘上的某个目录,不需要进行安装程序中的任何步骤。用户只需要配置好环境变量(主要是PATH、JAVA_HOME等),就可以直接使用命令行工具来运行Java程序或编译代码。 4. 源码:在软件开发领域,源码指的是程序的原始代码,它是由程序员编写的可读文本,通常是高级编程语言如Java、C++等的代码。本压缩包附带的源码允许开发者阅读和研究Java类库是如何实现的,有助于深入理解Java语言的内部工作原理。源码对于学习、调试和扩展Java平台是非常有价值的资源。 5. 环境变量配置:环境变量是操作系统中用于控制程序执行环境的参数。在JDK中,常见的环境变量包括JAVA_HOME和PATH。JAVA_HOME是JDK安装目录的路径,配置此变量可以让操作系统识别到JDK的位置。PATH变量则用于指定系统命令查找的路径,将JDK的bin目录添加到PATH后,就可以在命令行中的任何目录下执行JDK中的命令,如javac和java。 在实际开发中,了解并正确配置JDK对于Java开发者来说是一个基础且重要的环节。掌握如何安装和配置JDK,以及如何理解JDK中的源码和各种工具,对于进行Java编程和解决问题至关重要。
管理建模和仿真的文件
管理Boualem Benatallah引用此版本:布阿利姆·贝纳塔拉。管理建模和仿真。约瑟夫-傅立叶大学-格勒诺布尔第一大学,1996年。法语。NNT:电话:00345357HAL ID:电话:00345357https://theses.hal.science/tel-003453572008年12月9日提交HAL是一个多学科的开放存取档案馆,用于存放和传播科学研究论文,无论它们是否被公开。论文可以来自法国或国外的教学和研究机构,也可以来自公共或私人研究中心。L’archive ouverte pluridisciplinaire
【提升效率与稳定性】:深入掌握单相整流器的控制策略
# 摘要 单相整流器作为电力电子技术的基础设备,广泛应用于电力系统和工业自动化领域。本文首先概述了单相整流器的基本概念,详细分析了其工作原理,包括电力电子器件的角色、数学模型以及控制策略。随后,针对控制技术进行了深入探讨,包括传统控制技术如PID控制和高级控制策略如模糊逻辑控制及自适应控制的应用。进一步地,本文提出了一系列提升单相整流器性能的方法,如效率提升策略、系统稳定性措施,以及性能评估与优化方案。最后,文章探讨了单相整流器在不同领域的应用案例,并对新兴技术与市场趋势进行了展望。 # 关键字 单相整流器;电力电子器件;数学模型;控制策略;性能提升;应用案例 参考资源链接:[单相PWM整
你看这是ashx映射的cs文件初始代码,你看这里边根本就没有写对action参数进行任何操作但你.ashx?action=submit这样去做他就能返回出数据这是为什么
在ASP.NET中,.ashx文件(也称为HTTP处理程序)用于处理HTTP请求并返回响应。即使在初始代码中没有对action参数进行任何操作,系统仍然可以通过默认的ProcessRequest方法处理请求并返回数据。 当你在URL中传递参数(如?action=submit)时,这些参数会被包含在请求的查询字符串中。虽然你的代码没有显式地处理这些参数,但默认的ProcessRequest方法会接收这些参数并执行一些默认操作。 以下是一个简单的.ashx文件示例: ```csharp <%@ WebHandler Language="C#" Class="MyHandler" %> us
机器学习预测葡萄酒评分:二值化品尝笔记的应用
资源摘要信息:"wine_reviewer:使用机器学习基于二值化的品尝笔记来预测葡萄酒评论分数" 在当今这个信息爆炸的时代,机器学习技术已经被广泛地应用于各个领域,其中包括食品和饮料行业的质量评估。在本案例中,将探讨一个名为wine_reviewer的项目,该项目的目标是利用机器学习模型,基于二值化的品尝笔记数据来预测葡萄酒评论的分数。这个项目不仅对于葡萄酒爱好者具有极大的吸引力,同时也为数据分析和机器学习的研究人员提供了实践案例。 首先,要理解的关键词是“机器学习”。机器学习是人工智能的一个分支,它让计算机系统能够通过经验自动地改进性能,而无需人类进行明确的编程。在葡萄酒评分预测的场景中,机器学习算法将从大量的葡萄酒品尝笔记数据中学习,发现笔记与葡萄酒最终评分之间的相关性,并利用这种相关性对新的品尝笔记进行评分预测。 接下来是“二值化”处理。在机器学习中,数据预处理是一个重要的步骤,它直接影响模型的性能。二值化是指将数值型数据转换为二进制形式(0和1)的过程,这通常用于简化模型的计算复杂度,或者是数据分类问题中的一种技术。在葡萄酒品尝笔记的上下文中,二值化可能涉及将每种口感、香气和外观等属性的存在与否标记为1(存在)或0(不存在)。这种方法有利于将文本数据转换为机器学习模型可以处理的格式。 葡萄酒评论分数是葡萄酒评估的量化指标,通常由品酒师根据酒的品质、口感、香气、外观等进行评分。在这个项目中,葡萄酒的品尝笔记将被用作特征,而品酒师给出的分数则是目标变量,模型的任务是找出两者之间的关系,并对新的品尝笔记进行分数预测。 在机器学习中,通常会使用多种算法来构建预测模型,如线性回归、决策树、随机森林、梯度提升机等。在wine_reviewer项目中,可能会尝试多种算法,并通过交叉验证等技术来评估模型的性能,最终选择最适合这个任务的模型。 对于这个项目来说,数据集的质量和特征工程将直接影响模型的准确性和可靠性。在准备数据时,可能需要进行数据清洗、缺失值处理、文本规范化、特征选择等步骤。数据集中的标签(目标变量)即为葡萄酒的评分,而特征则来自于品酒师的品尝笔记。 项目还提到了“kaggle”和“R”,这两个都是数据分析和机器学习领域中常见的元素。Kaggle是一个全球性的数据科学竞赛平台,提供各种机器学习挑战和数据集,吸引了来自全球的数据科学家和机器学习专家。通过参与Kaggle竞赛,可以提升个人技能,并有机会接触到最新的机器学习技术和数据处理方法。R是一种用于统计计算和图形的编程语言和软件环境,它在统计分析、数据挖掘、机器学习等领域有广泛的应用。使用R语言可以帮助研究人员进行数据处理、统计分析和模型建立。 至于“压缩包子文件的文件名称列表”,这里可能存在误解或打字错误。通常,这类名称应该表示存储项目相关文件的压缩包,例如“wine_reviewer-master.zip”。这个压缩包可能包含了项目的源代码、数据集、文档和其它相关资源。在开始项目前,研究人员需要解压这个文件包,并且仔细阅读项目文档,以便了解项目的具体要求和数据格式。 总之,wine_reviewer项目是一个结合了机器学习、数据处理和葡萄酒品鉴的有趣尝试,它不仅展示了机器学习在实际生活中的应用潜力,也为研究者提供了丰富的学习资源和实践机会。通过这种跨领域的合作,可以为葡萄酒行业带来更客观、一致的评价标准,并帮助消费者做出更加明智的选择。
"互动学习:行动中的多样性与论文攻读经历"
多样性她- 事实上SCI NCES你的时间表ECOLEDO C Tora SC和NCESPOUR l’Ingén学习互动,互动学习以行动为中心的强化学习学会互动,互动学习,以行动为中心的强化学习计算机科学博士论文于2021年9月28日在Villeneuve d'Asq公开支持马修·瑟林评审团主席法布里斯·勒菲弗尔阿维尼翁大学教授论文指导奥利维尔·皮耶昆谷歌研究教授:智囊团论文联合主任菲利普·普雷教授,大学。里尔/CRISTAL/因里亚报告员奥利维耶·西格德索邦大学报告员卢多维奇·德诺耶教授,Facebook /索邦大学审查员越南圣迈IMT Atlantic高级讲师邀请弗洛里安·斯特鲁布博士,Deepmind对于那些及时看到自己错误的人...3谢谢你首先,我要感谢我的两位博士生导师Olivier和Philippe。奥利维尔,"站在巨人的肩膀上"这句话对你来说完全有意义了。从科学上讲,你知道在这篇论文的(许多)错误中,你是我可以依
【单相整流器终极指南】:电气工程师的20年实用技巧大揭秘
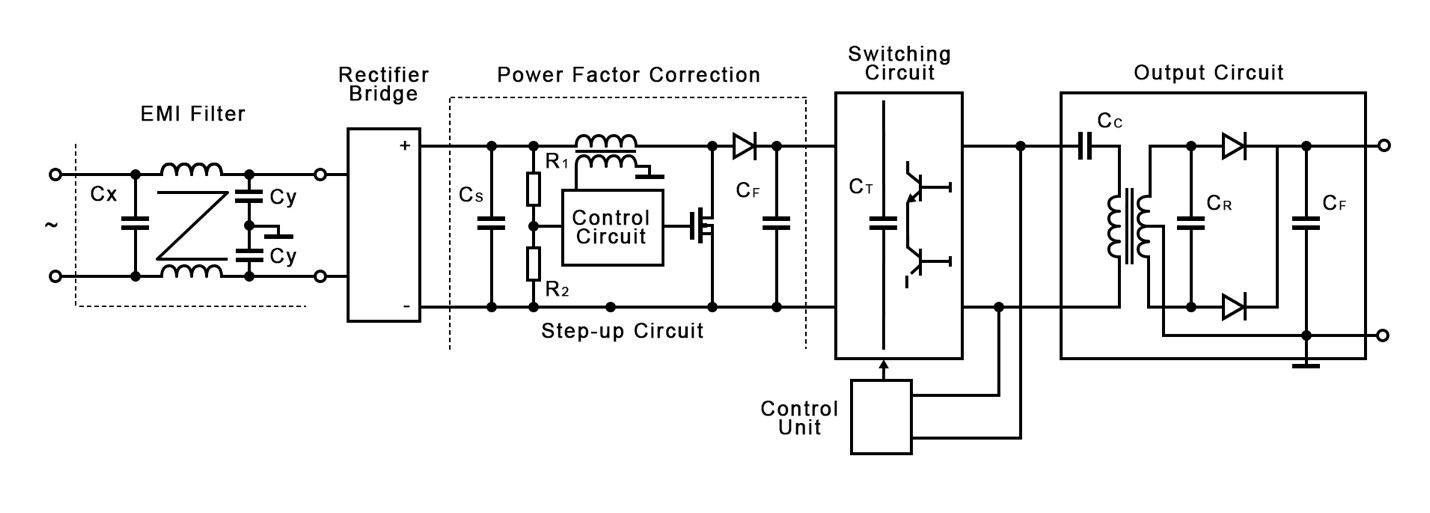 # 摘要 单相整流器是电力电子技术中应用广泛的设备,用于将交流电转换为直流电。本文首先介绍了单相整流器的基础知识和工作原理,分析了其设计要点,性能评估方法以及在电力系统和电子设备中的应用。接着,探讨了单相整流器的进阶应用和优化策略,包括提高效率和数字化改造。文章还通过具体案例分析,展示了单