首页信息论与编码huffman编码
信息论与编码huffman编码
时间: 2023-07-10 19:41:56 浏览: 59
好的,你想了解关于信息论和编码中的Huffman编码,是吗?
首先,信息论是一门研究信息传输和处理的学科,它的主要任务是研究信息的量、质和传输的效率等问题。编码技术则是信息论的一个重要分支,它通过对信息进行编码和解码,实现信息的传输和处理。
Huffman编码是一种常用的无损数据压缩编码技术,它通过建立一个字符集的二叉树来实现编码。在Huffman编码中,每个字符都由一个唯一的二进制编码表示,编码长度与该字符出现的频率成反比。这样,在压缩数据时,出现频率较高的字符将会被分配一个较短的编码,而出现频率较低的字符将会被分配一个较长的编码,从而实现数据的压缩和解压缩。
Huffman编码被广泛应用于数据压缩和网络传输中,它可以大大减少数据的存储和传输成本,提高数据传输效率。
CSDN会员
开通CSDN年卡参与万元壕礼抽奖
最新推荐
信息论与编码课程设计实验报告java
基于java的n元huffman编码及其译码,基于java的与huffman编码相结合的游程编码。 其中包括实现思想,实验源代码,实验截图等。
信息论与编码实验报告(含代码 哈弗曼编码 香农编码)
1. 在VC6.0的环境下实现Huffman编码; 2. 在VC6.0的环境下实现Shannon编码; 3. 在VC6.0的环境下实现4个数的全排列。
node-v10.9.0-x86.msi
Node.js,简称Node,是一个开源且跨平台的JavaScript运行时环境,它允许在浏览器外运行JavaScript代码。Node.js于2009年由Ryan Dahl创立,旨在创建高性能的Web服务器和网络应用程序。它基于Google Chrome的V8 JavaScript引擎,可以在Windows、Linux、Unix、Mac OS X等操作系统上运行。
Node.js的特点之一是事件驱动和非阻塞I/O模型,这使得它非常适合处理大量并发连接,从而在构建实时应用程序如在线游戏、聊天应用以及实时通讯服务时表现卓越。此外,Node.js使用了模块化的架构,通过npm(Node package manager,Node包管理器),社区成员可以共享和复用代码,极大地促进了Node.js生态系统的发展和扩张。
Node.js不仅用于服务器端开发。随着技术的发展,它也被用于构建工具链、开发桌面应用程序、物联网设备等。Node.js能够处理文件系统、操作数据库、处理网络请求等,因此,开发者可以用JavaScript编写全栈应用程序,这一点大大提高了开发效率和便捷性。
在实践中,许多大型企业和组织已经采用Node.js作为其Web应用程序的开发平台,如Netflix、PayPal和Walmart等。它们利用Node.js提高了应用性能,简化了开发流程,并且能更快地响应市场需求。
塞北村镇旅游网站设计与实现
城市旅游产业的日新月异影响着村镇旅游产业的发展变化。网络、电子科技的迅猛前进同样牵动着旅游产业的快速成长。随着人们消费理念的不断发展变化,越来越多的人开始注意精神文明的追求,而不仅仅只是在意物质消费的提高。塞北村镇旅游网站的设计就是帮助村镇发展旅游产业,达到宣传效果,带动一方经济发展。而在线消费与查询正在以高效,方便,时尚等的特点成为广大互联网用户的首选。塞北村镇旅游网站设计与开发以方便、快捷、费用低的优点正慢慢地进入人们的生活。人们从传统的旅游方式转变为在线预览,减轻了劳动者的工作量。使得旅游从业人员有更多时间来获取、了解、掌握信息。
塞北村镇旅游网站根据当地旅游风景和特色的实际情况,设计出一套适合当地旅游信息网站,通过网络,实现该网站的推广从而达到宣传的效果。
本系统在设计方面采用JSP和Java语言以及html脚本语言,同时采用B/S模式,进行各个界面和每个功能的设计与实现,后台管理与设计选用了SQL Server 2005数据库,前台设计与后台管理相结合,共同完成各功能模块的功能。
其他类别Jsp考试系统-jspks.rar
JSP考试系统_jspks.rar是一个为计算机专业学生和教师设计的JSP源码资料包,它提供了一个全面的、易于使用的在线考试平台。这个系统是基于Java Server Pages (JSP)技术构建的,这是一种用于创建动态网页的服务器端技术。通过这个系统,用户可以创建、管理和参加在线考试。这个系统的主要功能包括:用户注册和登录,试题管理(包括添加、修改和删除试题),试卷管理(包括创建、编辑和删除试卷),考试管理(包括开始、暂停和结束考试),成绩管理(包括查看和统计成绩)等。此外,系统还提供了丰富的试题类型,如选择题、填空题、判断题和简答题等,以满足不同的考试需求。JSP考试系统的界面设计简洁明了,操作方便,无论是教师还是学生都可以轻松上手。对于教师来说,他们可以通过这个系统轻松地管理试题和试卷,节省了大量的时间和精力。对于学生来说,他们可以随时随地参加在线考试,方便快捷。总的来说,JSP考试系统_jspks.rar是一个非常实用的JSP源码资料包,它不仅可以帮助学生更好地学习和掌握JSP技术,也可以帮助教师更有效地管理在线考试。无论是对于学生还是教师,这个系统都是一个不可或缺的工具。重
RTL8188FU-Linux-v5.7.4.2-36687.20200602.tar(20765).gz
REALTEK 8188FTV 8188eus 8188etv linux驱动程序稳定版本, 支持AP,STA 以及AP+STA 共存模式。 稳定支持linux4.0以上内核。
管理建模和仿真的文件
管理Boualem Benatallah引用此版本:布阿利姆·贝纳塔拉。管理建模和仿真。约瑟夫-傅立叶大学-格勒诺布尔第一大学,1996年。法语。NNT:电话:00345357HAL ID:电话:00345357https://theses.hal.science/tel-003453572008年12月9日提交HAL是一个多学科的开放存取档案馆,用于存放和传播科学研究论文,无论它们是否被公开。论文可以来自法国或国外的教学和研究机构,也可以来自公共或私人研究中心。L’archive ouverte pluridisciplinaire
:YOLOv1目标检测算法:实时目标检测的先驱,开启计算机视觉新篇章
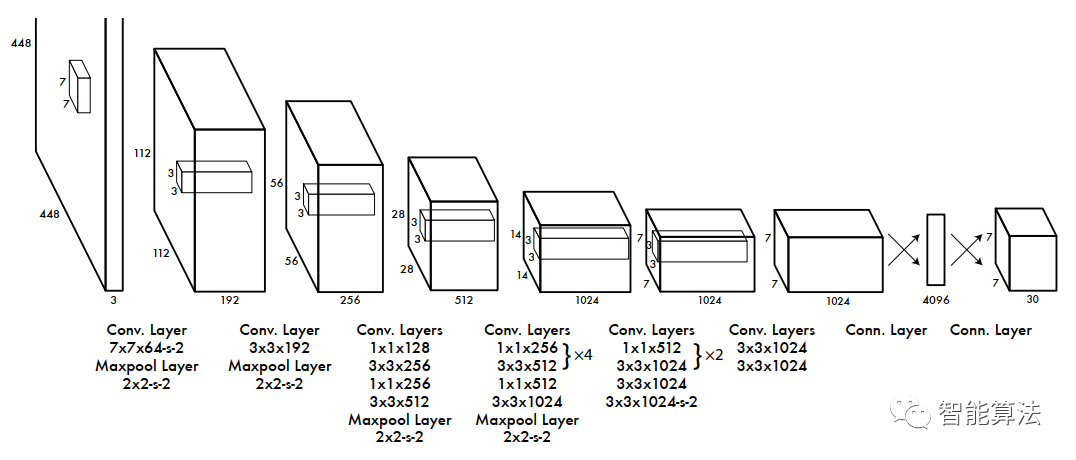
# 1. 目标检测算法概述
目标检测算法是一种计算机视觉技术,用于识别和定位图像或视频中的对象。它在各种应用中至关重要,例如自动驾驶、视频监控和医疗诊断。
目标检测算法通常分为两类:两阶段算法和单阶段算法。两阶段算法,如 R-CNN 和 Fast R-CNN,首先生成候选区域,然后对每个区域进行分类和边界框回归。单阶段算法,如 YOLO 和 SSD,一次性执行检
info-center source defatult
这是一个 Cisco IOS 命令,用于配置 Info Center 默认源。Info Center 是 Cisco 设备的日志记录和报告工具,可以用于收集和查看设备的事件、警报和错误信息。该命令用于配置 Info Center 默认源,即设备的默认日志记录和报告服务器。在命令行界面中输入该命令后,可以使用其他命令来配置默认源的 IP 地址、端口号和协议等参数。
c++校园超市商品信息管理系统课程设计说明书(含源代码) (2).pdf
校园超市商品信息管理系统课程设计旨在帮助学生深入理解程序设计的基础知识,同时锻炼他们的实际操作能力。通过设计和实现一个校园超市商品信息管理系统,学生掌握了如何利用计算机科学与技术知识解决实际问题的能力。在课程设计过程中,学生需要对超市商品和销售员的关系进行有效管理,使系统功能更全面、实用,从而提高用户体验和便利性。
学生在课程设计过程中展现了积极的学习态度和纪律,没有缺勤情况,演示过程流畅且作品具有很强的使用价值。设计报告完整详细,展现了对问题的深入思考和解决能力。在答辩环节中,学生能够自信地回答问题,展示出扎实的专业知识和逻辑思维能力。教师对学生的表现予以肯定,认为学生在课程设计中表现出色,值得称赞。
整个课程设计过程包括平时成绩、报告成绩和演示与答辩成绩三个部分,其中平时表现占比20%,报告成绩占比40%,演示与答辩成绩占比40%。通过这三个部分的综合评定,最终为学生总成绩提供参考。总评分以百分制计算,全面评估学生在课程设计中的各项表现,最终为学生提供综合评价和反馈意见。
通过校园超市商品信息管理系统课程设计,学生不仅提升了对程序设计基础知识的理解与应用能力,同时也增强了团队协作和沟通能力。这一过程旨在培养学生综合运用技术解决问题的能力,为其未来的专业发展打下坚实基础。学生在进行校园超市商品信息管理系统课程设计过程中,不仅获得了理论知识的提升,同时也锻炼了实践能力和创新思维,为其未来的职业发展奠定了坚实基础。
校园超市商品信息管理系统课程设计的目的在于促进学生对程序设计基础知识的深入理解与掌握,同时培养学生解决实际问题的能力。通过对系统功能和用户需求的全面考量,学生设计了一个实用、高效的校园超市商品信息管理系统,为用户提供了更便捷、更高效的管理和使用体验。
综上所述,校园超市商品信息管理系统课程设计是一项旨在提升学生综合能力和实践技能的重要教学活动。通过此次设计,学生不仅深化了对程序设计基础知识的理解,还培养了解决实际问题的能力和团队合作精神。这一过程将为学生未来的专业发展提供坚实基础,使其在实际工作中能够胜任更多挑战。