MATLAB插值函数在科学计算中的应用：解决复杂数学问题的利器

# 1. MATLAB插值函数简介

MATLAB插值函数是一种强大的工具，用于估计未采样点的数据值。它在科学计算、工程和数据分析等广泛领域中有着重要的应用。插值函数通过使用已知数据点来近似未知数据点，从而实现数据的平滑和预测。

MATLAB提供了各种插值函数，包括线性插值、多项式插值、双线性插值和双二次插值。这些函数可以处理一维和二维数据，并支持各种边界条件和插值方法。通过选择合适的插值函数和参数，可以实现高精度的插值结果，满足不同的应用需求。

# 2. MATLAB插值函数的理论基础

### 2.1 插值概念和数学原理

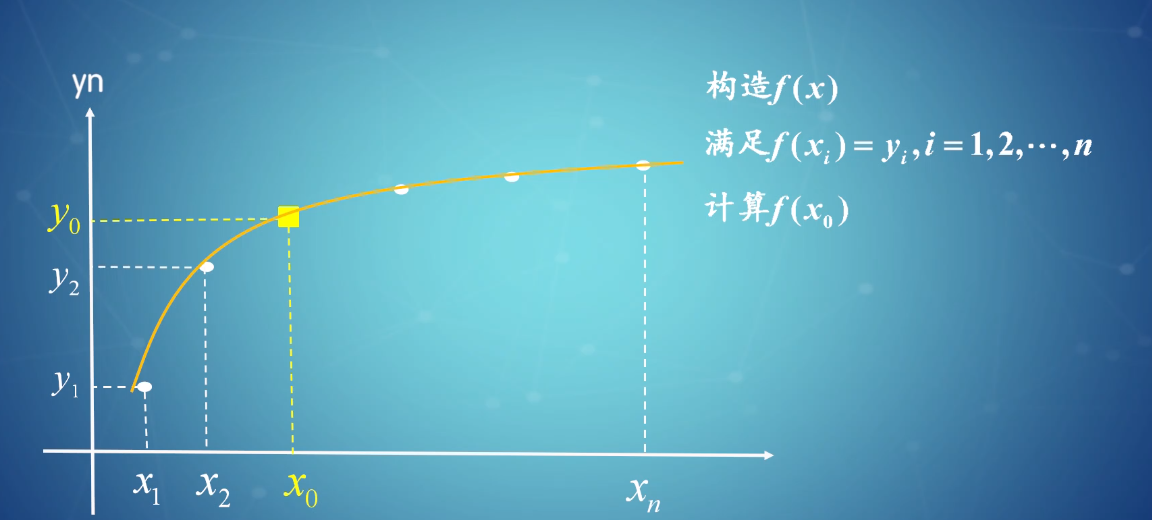
**插值**是一种数学技术，用于根据已知数据点估计未知数据点。在MATLAB中，插值函数通过使用数学公式来创建平滑曲线或曲面，该曲线或曲面穿过已知数据点。

插值的数学原理基于**泰勒展开式**。泰勒展开式可以将一个函数在某个点附近的函数值表示为一个多项式。对于插值，我们使用多项式来逼近未知数据点。

### 2.2 常见的插值方法

MATLAB提供了多种插值方法，每种方法都有其独特的优点和缺点。常见的插值方法包括：

- **线性插值：**使用两条已知数据点之间的直线来估计未知数据点。
- **多项式插值：**使用低阶多项式来拟合已知数据点，然后使用该多项式来估计未知数据点。
- **样条插值：**使用分段多项式来拟合已知数据点，从而产生一个光滑的曲线。
- **径向基插值：**使用径向基函数来估计未知数据点，该函数基于已知数据点到未知数据点的距离。

#### 2.2.1 线性插值

线性插值是最简单的插值方法。它使用两条已知数据点之间的直线来估计未知数据点。

% 已知数据点
x = [1, 2, 3];
y = [2, 4, 6];

% 要插值的数据点
x_new = 1.5;

% 线性插值
y_new = interp1(x, y, x_new);

% 输出插值结果
fprintf('插值结果：%.2f\n', y_new);

**逻辑分析：**

* `interp1` 函数用于执行线性插值。
* `x` 和 `y` 是已知数据点的 x 和 y 坐标。
* `x_new` 是要插值的数据点的 x 坐标。
* `y_new` 是插值结果。

#### 2.2.2 多项式插值

多项式插值使用低阶多项式来拟合已知数据点。

% 已知数据点
x = [1, 2, 3, 4];
y = [2, 4, 6, 8];

% 要插值的数据点
x_new = 2.5;

% 多项式插值
p = polyfit(x, y, 3); % 拟合一个三阶多项式
y_new = polyval(p, x_new);

% 输出插值结果
fprintf('插值结果：%.2f\n', y_new);

**逻辑分析：**

* `polyfit` 函数用于拟合多项式。
* `x` 和 `y` 是已知数据点的 x 和 y 坐标。
* `3` 指定多项式的阶数。
* `p` 是拟合的多项式系数。
* `polyval` 函数用于计算多项式在 `x_new` 处的函数值。
* `y_new` 是插值结果。

# 3. MATLAB插值函数的实践应用

### 3.1 一维插值函数的使用

一维插值函数用于对一维数据进行插值，即在已知数据点之间插入新的数据点。MATLAB提供了多种一维插值函数，包括线性插值和多项式插值。

#### 3.1.1 线性插值

线性插值是最简单的一维插值方法，它假设相邻数据点之间的函数值变化是线性的。MATLAB中使用`interp1`函数进行线性插值，其语法如下：

yi = interp1(x, y, xi)

其中：

* `x`：已知数据点的自变量值向量
* `y`：已知数据点的因变量值向量
* `xi`：需要插值的自变量值向量
* `yi`：插值后的因变量值向量

**代码块：**

% 已知数据点
x = [0, 1, 2, 3];
y = [0, 1, 4, 9];

% 需要插值的自变量值
xi = 1.5;

% 线性插值
yi = interp1(x, y, xi);

% 输出插值结果
fprintf('插值结果：%.2f\n', yi);

**逻辑分析：**

该代码块使用`interp1`函数对已知数据点进行线性插值。`x`和`y`向量分别表示自变量值和因变量值，`xi`表示需要插值的自变量值。`interp1`函数返回插值后的因变量值`yi`，并输出插值结果。

#### 3.1.2 多项式插值

多项式插值使用多项式函数拟合已知数据点，然后使用该多项式函数进行插值。MATLAB中使用`polyfit`和`polyval`函数进行多项式插值，其语法如下：

% 多项式拟合
p = polyfit(x, y, n);

% 多项式插值
yi = polyval(p, xi);

其中：

* `x`：已知数据点的自变量值向量
* `y`：已知数据点的因变量值向量
* `n`：多项式的阶数
* `