排序算法的稳定性分析：稳定排序与不稳定排序，专家级别的编码选择

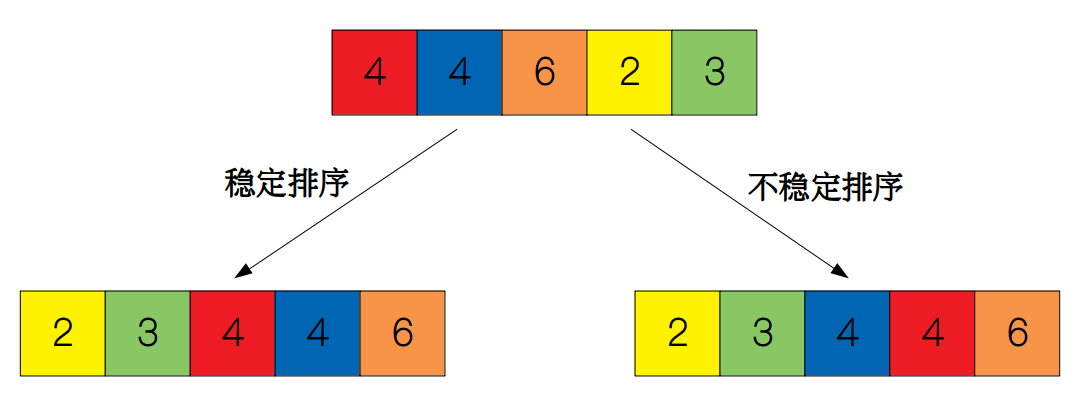
# 1. 排序算法的基础与分类

排序算法是编程中的基础内容，也是衡量一个开发者能力的标尺之一。在数据处理的众多场景中，排序算法的运用极为广泛，因此了解排序算法的基础知识以及分类是每个IT专业人士的必备技能。

## 1.1 排序算法的基本概念

排序算法的基本目的是对一组数据按照特定的顺序重新排列。这在数据库查询、数据挖掘和用户界面中非常重要。排序不仅涉及到数据的外观，还影响到数据处理的效率。

## 1.2 排序算法的性能指标

通常，我们用时间复杂度和空间复杂度来衡量排序算法的性能。时间复杂度描述了算法完成排序任务所需时间与输入数据规模之间的关系，而空间复杂度则反映了算法在执行过程中临时需要占用的存储空间大小。

## 1.3 排序算法的分类

排序算法可以被分类为比较排序和非比较排序。比较排序依赖比较元素之间的大小关系进行排序，例如快速排序、归并排序；非比较排序不依赖比较操作，如计数排序、桶排序。进一步地，比较排序可以分为稳定的和不稳定的，而稳定排序算法能够保证具有相同值的元素在排序后保持原有的顺序。

通过理解这些基本概念和性能指标，我们为进一步学习和讨论各种具体排序算法打下了坚实的基础。接下来，我们将深入探索稳定排序算法的理论与实践。

# 2. 稳定排序算法的理论与实践

### 2.1 稳定排序算法的定义和重要性

稳定排序算法在处理具有相同排序关键字的元素时，会保持它们在原始数据中的相对顺序。这一特性在很多实际应用中极为重要，比如在多字段排序时，保持某些字段的相对顺序，或在稳定性对于结果正确性至关重要的场景。

#### 2.1.1 稳定排序的理论基础

从理论层面讲，稳定排序算法关注的是排序过程中元素之间的相对位置。在数学上，一个排序算法被认为是稳定的，如果对于任意两个相等的元素 `A` 和 `B`，如果在输入序列中 `A` 出现在 `B` 前面，那么在排序后的序列中 `A` 仍然应该出现在 `B` 的前面。

#### 2.1.2 稳定性对排序结果的影响

稳定性对于最终排序结果的影响主要表现在如下几个方面：

1. **数据处理：** 在数据处理的场景中，例如数据库查询结果排序，稳定排序能确保具有相同排序关键字的记录保持它们在数据集中的原始顺序，这有利于数据的进一步分析。
2. **复杂排序：** 当需要根据多个关键字进行排序时，稳定排序可以首先根据一个关键字进行稳定排序，然后对结果再按照下一个关键字进行稳定排序。这种方法使得最终排序结果符合多个关键字的排序需求。

### 2.2 常见稳定排序算法解析

在众多排序算法中，一些算法天然具有稳定性。以下是最为常见的几种稳定排序算法的详细解析。

#### 2.2.1 归并排序的原理及实现

归并排序是一种分治算法，核心在于将输入数据分成大小相同的两半，分别进行排序后，再将排序好的两部分合并成一个最终的排序序列。归并排序的稳定性来源于合并过程中对元素的处理方式。

def merge_sort(arr):
    if len(arr) > 1:
        mid = len(arr) // 2
        L = arr[:mid]
        R = arr[mid:]

        merge_sort(L)
        merge_sort(R)

        i = j = k = 0

        while i < len(L) and j < len(R):
            if L[i] <= R[j]:
                arr[k] = L[i]
                i += 1
            else:
                arr[k] = R[j]
                j += 1
            k += 1

        while i < len(L):
            arr[k] = L[i]
            i += 1
            k += 1

        while j < len(R):
            arr[k] = R[j]
            j += 1
            k += 1

    return arr

# 示例数组
arr = [38, 27, 43, 3, 9, 82, 10]
sorted_arr = merge_sort(arr)
print(sorted_arr)

上面的代码段展示了归并排序的基本实现。归并排序的每一步操作都保证了原有相等元素的相对顺序不会改变，从而确保了其稳定性。

#### 2.2.2 插入排序的优势与应用

插入排序是一种简单直观的排序算法。对于一个未排序的数据，它会将数据分为已排序和未排序两部分，每次从未排序部分取出第一个元素，在已排序部分中找到合适的位置将其插入，直到未排序部分为空。

def insertion_sort(arr):
    for i in range(1, len(arr)):
        key = arr[i]
        j = i - 1
        while j >= 0 and key < arr[j]:
            arr[j + 1] = arr[j]
            j -= 1
        arr[j + 1] = key
    return arr

# 示例数组
arr = [38, 27, 43, 3, 9, 82, 10]
sorted_arr = insertion_sort(arr)
print(sorted_arr)

插入排序的优势在于其简单性和在部分情况下的高效性。它是最适合小规模数据集的排序方法之一，同时由于其稳定性，在某些应用中它比其他更为复杂的算法更受欢迎。

#### 2.2.3 堆排序的稳定性探讨

堆排序是一种选择排序，通过构建堆这种数据结构进行排序，但堆排序本身并不稳定。在构建堆的过程中，可能会破坏相等元素的原始顺序。但是，通过一些策略，例如在构建堆时使用特定的比较器来维护稳定性，可以实现稳定版本的堆排序。

def heapify(arr, n, i):
    largest = i
    l = 2 * i + 1
    r = 2 * i + 2

    if l < n and arr[i] < arr[l]:
        largest = l

    if r < n and arr[largest] < arr[r]:
        largest = r

    if largest != i:
        arr[i], arr[largest] = arr[largest], arr[i]
        heapify(arr, n, largest)

def heap_sort(arr):
    n = len(arr)
    for i in range(n // 2 - 1, -1, -1):
        heapify(arr, n, i)

    for i in range(n - 1, 0, -1):
        arr[i], arr[0] = arr[0], arr[i]
        heapify(arr, i, 0)

    return arr

# 示例数组
arr = [38, 27, 43, 3, 9, 82, 10]
sorted_arr = heap_sort(arr)
print(sorted_arr)

堆排序通常不如其他稳定排序算法受欢迎，但是在需要快速排序大数组时，它是一个可行的选择。对于稳定性有要求的应用场景，堆排序可能不是最佳选择，除非能保证通过其他方式弥补其不稳定性。

### 2.3 稳定排序算法的性能优化

稳定排序算法虽然在很多应用中至关重要，但它们的性能通常比不稳定排序算法要差。优化稳定排序算法的性能，对于实际应用来说是一个非常重要的研究课题。

#### 2.3.1 算法时间复杂度分析

稳定排序算法的常见时间复杂度包括 `O(n^2)` 和 `O(n log n)`，其中 `O(n log n)` 的算法往往性能更好，尤其是对于大规模数据集。在实现稳定排序算法时，优化的重点通常在于减少比较和交换操作的次数。

#### 2.3.2 空间复杂度与效率权衡

在考虑稳定排序算法的性能优化时，空间复杂度也是一个不容忽视的因素。例如，归并排序的空间复杂度为 `O(n)`，如果输入数据非常庞大，可能会造成内存使用上的压力。因此，优化稳定排序算法时，找到时间和空间复杂度之间的最佳平衡点是关键。

graph TD
    A[稳定排序算法] --> B[时间复杂度分析]
    A --> C[空间复杂度考虑]
    B --> D[比较次数优化]
    B --> E[递归深度优化]
    C --> F[内存管理优化]
    C --> G[外部存储利用]

优化稳定排序算法的性能，往往需要通过算法设计和实现细节的不断打磨。在实际应用中，可能需要根据数据特性和具体需