OpenFOAM湍流模型选择指南：精确模拟的关键决策


# 摘要
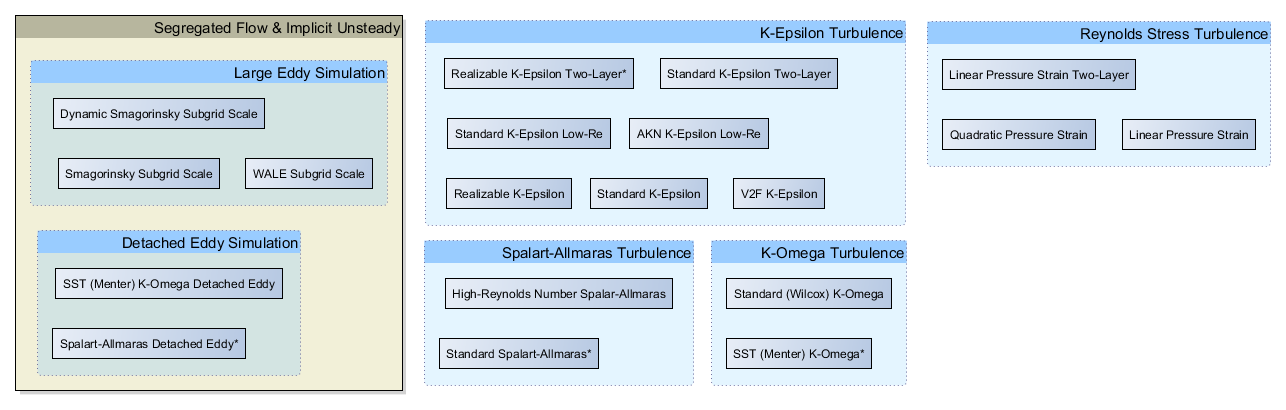
OpenFOAM是一个强大的开源计算流体动力学(CFD)工具，广泛应用于湍流模型的研究和工程实践中。本文首先介绍了OpenFOAM及其在湍流模型方面的应用，然后深入探讨了湍流模型的理论基础，包括RANS、LES和DNS模型的分类及其选择标准。随后，本文详细解析了湍流模型在OpenFOAM中的配置、求解流程以及后处理分析方法，强调了模型参数设置和求解策略的重要性。案例实践章节通过具体案例分析，阐述了如何优化和调整湍流模型以适应不同物理问题。最后，本文展望了湍流模型研究的前沿方向，如数据驱动模型、多尺度多物理场耦合模型，以及OpenFOAM在湍流研究中的应用前景，探讨了精确模拟与工业应用的结合和挑战。

# 关键字
OpenFOAM；湍流模型；RANS；LES；DNS；后处理分析

参考资源链接：[OpenFOAM编程指南中文版.pdf](https://wenku.csdn.net/doc/6412b4b4be7fbd1778d40866?spm=1055.2635.3001.10343)
# 1. OpenFOAM与湍流模型简介

OpenFOAM（Open Field Operation and Manipulation）是一个强大的计算流体动力学（CFD）工具，它提供了丰富的求解器和功能强大的库来模拟和分析复杂的流体问题。在CFD领域，湍流模型作为解决实际流动问题的关键组件，扮演着至关重要的角色。本章将简介OpenFOAM的基础知识，并引入湍流模型的概念，为后续章节深入讨论各类湍流模型的理论和应用打下基础。

OpenFOAM的强大之处在于其开源特性，这意味着研究者和工程师可以自由地修改和扩展其功能，以适应各种特殊的计算需求。OpenFOAM支持广泛的湍流模型，从简单的雷诺平均Navier-Stokes（RANS）模型到复杂的LES（大涡模拟）和DNS（直接数值模拟）模型，适用于不同的流动场景和精确度需求。湍流问题的解决对航空、汽车、建筑、能源等多个行业的设计与优化至关重要。

理解湍流模型，需要从流体动力学的基本原理入手，特别是雷诺应力和Navier-Stokes方程的深入研究。下一章将详细探讨湍流模型的理论基础，揭示其分类，并解释为何选择特定的湍流模型对预测流动特性具有决定性意义。随着讨论的深入，我们将逐步探索如何在OpenFOAM中配置、求解和分析湍流模型。

# 2. ```
# 第二章：湍流模型理论基础
本章将深入探讨湍流模型的理论基础，为理解后续章节中湍流模型在OpenFOAM中的实现和应用奠定坚实的理论基础。内容从湍流模型的基本分类开始，逐步阐述如何选择合适的湍流模型，再到深入分析几种常见的湍流模型理论。

## 2.1 湍流模型分类概述
湍流模型可以从不同的角度进行分类，本节将对主要的湍流模型分类进行介绍，并简要分析它们的特点。

### 2.1.1 雷诺平均Navier-Stokes(RANS)模型
雷诺平均Navier-Stokes（RANS）模型是基于将速度场分解为平均流和脉动流的假设，通过对脉动流的相关统计量进行建模来模拟湍流流动。RANS模型包括很多不同的子模型，如k-epsilon模型、k-omega模型和Reynolds Stress Model (RSM)等，它们各有适用场合。

flowchart LR
    RANS[雷诺平均Navier-Stokes模型] --> k-epsilon[k-epsilon模型]
    RANS --> k-omega[k-omega模型]
    RANS --> RSM[Reynolds Stress Model]
    k-epsilon --> 适用[典型应用]
    k-omega --> 适用
    RSM --> 适用

### 2.1.2 大涡模拟(LES)模型
大涡模拟（LES）是通过直接模拟大尺度的涡流来捕捉流动的湍流特性，而小尺度的涡流则通过次网格尺度（sub-grid scale）模型进行建模。LES模型因其能够模拟更复杂的流动结构而受到青睐，但计算成本相对较高。

### 2.1.3 直接数值模拟(DNS)
直接数值模拟（DNS）是一种理论上的湍流模拟方法，它尝试直接求解Navier-Stokes方程来模拟所有尺度上的涡流。DNS提供最精确的湍流流动描述，但由于其计算成本极高，目前仅限于简单几何形状和低雷诺数的流动。

## 2.2 湍流模型的选择标准
正确选择湍流模型对于数值模拟的成功至关重要。本节将分析选择湍流模型时需要考虑的几个关键因素。

### 2.2.1 物理问题特性
湍流模型的选择首先应基于物理问题本身的特性，比如流体的流速范围、是否有热交换、流动的稳定性等。不同物理特性的问题可能需要不同的模型来准确描述。

### 2.2.2 数值模拟资源限制
计算资源是选择湍流模型时不可忽视的因素。RANS模型通常适用于资源有限的情况，而LES和DNS则需要更高的计算能力。评估计算资源和预期结果的精度是平衡选择的重要步骤。

### 2.2.3 模型精度与计算效率的权衡
选择湍流模型涉及到模型精度与计算效率之间的权衡。高精度的模型如DNS能提供最准确的结果，但需要更长的计算时间。而高效率的模型如RANS在速度上有所优势，但可能牺牲一定的精度。因此，选择时需要根据实际需求来决定。

## 2.3 常见湍流模型的理论基础
本节将详细介绍几种常见的湍流模型的理论基础，以便读者能够更好地理解它们的工作原理和适用范围。

### 2.3.1 k-epsilon模型
k-epsilon模型是RANS模型中最常用的子模型之一，主要用于工程领域的湍流计算。它通过引入两个新的变量k和epsilon来表征湍流的脉动动能及其耗散率，从而对湍流进行模拟。

k-epsilon模型的控制方程可以表示为：
\frac{\partial}{\partial t}(\rho k) + \frac{\partial}{\partial x_i}(\rho k u_i) = \frac{\partial}{\partial x_j}\left[\left(\mu + \frac{\mu_t}{\sigma_k}\right)\frac{\partial k}{\partial x_j}\right] + G_k - \rho \epsilon
\frac{\partial}{\partial t}(\rho \epsilon) + \frac{\partial}{\partial x_i}(\rho \epsilon u_i) = \frac{\partial}{\partial x_j}\left[\left(\mu + \frac{\mu_t}{\sigma_\epsilon}\right)\frac{\partial \epsilon}{\partial x_j}\right] + C_{\epsilon 1} \frac{\epsilon}{k} G_k - C_{\epsilon 2} \rho \frac{\epsilon^2}{k}
其中，$G_k$ 是由于平均速度梯度产生的湍动能，$\mu_t$ 是湍流粘度，$\sigma_k$ 和 $\sigma_\epsilon$ 是模型常数。

### 2.3.2 k-omega模型
k-omega模型是另一种在RANS框架下的湍流模型，特别适合处理壁面附近的流动，因为它包含了一个针对近壁区流动的修正。模型中的omega变量与湍流耗散率相关。

### 2.3.3 Reynolds Stress Model (RSM)
Reynolds Stress Model (RSM) 是RANS模型中的一个高级形式，它考虑了湍流应力的各向异性特性。RSM直接模拟雷诺应力张量的传输方程，因此能够提供比k-epsilon和k-omega模型更精确的流场预测。然而，这也会导致计算上的复杂度增加。

在这一章节的结尾，我们将提供一个表格来总结这三种模型的优缺点和适用场景，以便读者更加直观地进行选择。

| 模型类型 | 优点 | 缺点 | 适用场景 |
| --- | --- | --- | --- |
| k-epsilon | 实现简单，计算速度快 | 精度较低，不适用于强旋流和强弯曲流 | 工程湍流计算 |
| k