MATLAB模拟退火算法应用大揭秘:原理、代码与案例
发布时间: 2024-12-16 01:08:17 阅读量: 1 订阅数: 3 


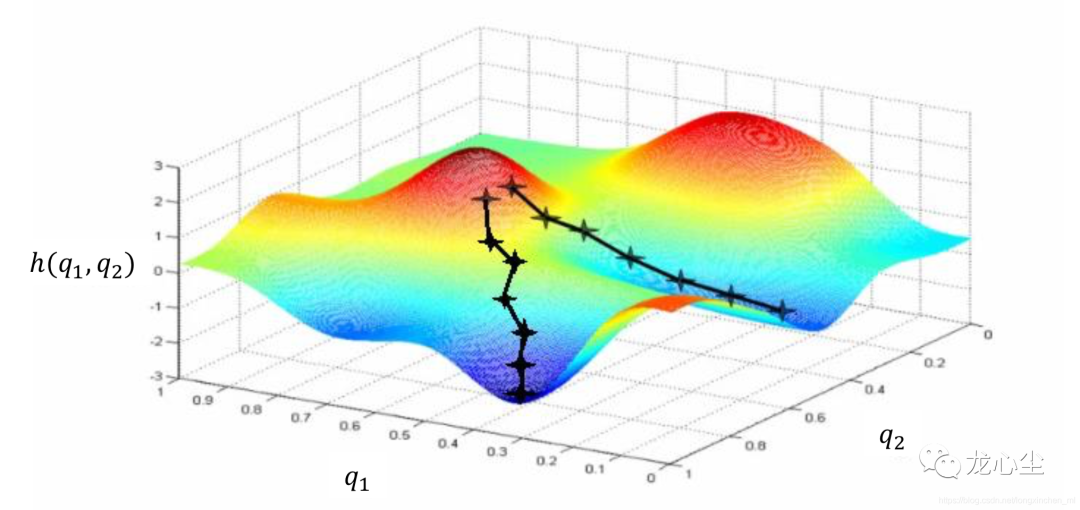
MATLAB模拟退火算法代码实例及其应用
参考资源链接:[最优化方法Matlab程序设计课后答案详解](https://wenku.csdn.net/doc/6472f573d12cbe7ec307a850?spm=1055.2635.3001.10343)
# 1. 模拟退火算法基础
## 1.1 模拟退火算法简介
模拟退火算法是一种启发式随机搜索算法,用于求解全局优化问题。灵感来源于固体物质退火过程,算法能够在搜索空间中随机“跳跃”,以概率接受更差的解,从而有效避免局部最优问题。
## 1.2 算法工作原理
模拟退火算法的核心在于模拟退火过程中温度的逐渐降低。初始时,温度较高,系统能量大,允许系统进行大规模的随机搜索。随着温度逐渐降低,搜索范围缩小,算法逐步收敛到全局最优解。
## 1.3 算法步骤与参数说明
算法主要步骤包括:初始化系统参数,如初始温度和冷却率;在每个温度下执行多次迭代搜索;按照一定的概率接受新的解。参数包括温度、冷却率、迭代次数等,这些参数需根据具体问题进行调整。
```mermaid
flowchart LR
A[初始化参数] --> B[高温随机搜索]
B --> C[逐步降温]
C --> D[收敛至最优解]
```
其中,**温度**控制算法的“跳跃”幅度,**冷却率**决定降温速度,**迭代次数**是每个温度下搜索的次数,这些都直接影响算法的效率和求解质量。
# 2. MATLAB环境搭建与算法实现
### MATLAB环境的安装与配置
在开始编写模拟退火算法之前,首先需要搭建一个合适的开发环境。MATLAB(矩阵实验室)是一个高级数学计算环境,广泛应用于数据分析、数值计算以及算法开发等众多领域。本节将详细介绍MATLAB环境的安装与配置。
#### 安装MATLAB
MATLAB的安装过程相对简单,以下是基本的安装步骤:
1. 访问MathWorks官方网站下载最新的MATLAB安装包。
2. 打开安装程序,同意软件许可协议。
3. 输入产品序列号,这可以在购买时获得。
4. 选择安装路径,注意确保有足够的磁盘空间。
5. 选择需要安装的产品组件,模拟退火算法实现通常需要MATLAB、Simulink以及相应工具箱。
6. 完成安装向导的其余步骤,系统将开始安装。
#### 配置MATLAB环境
安装完成后,需要对MATLAB环境进行一些基本配置,以确保算法能够顺利运行:
1. 打开MATLAB,通过Home选项卡中的"Set Path"按钮打开路径管理器。
2. 点击"Add Folder..."添加需要的自定义函数或脚本所在的文件夹路径。
3. 点击"Save"保存路径设置,并关闭路径管理器。
4. 设置工具箱路径,有些工具箱可能需要额外安装和配置。
5. 配置编译器,如果需要使用MATLAB与C或C++代码交互,可能需要配置编译器。
### 模拟退火算法的MATLAB实现
在MATLAB环境中搭建好开发平台后,我们就可以开始编写模拟退火算法了。以下是模拟退火算法在MATLAB中实现的一个基本框架,包括算法的主要函数与一些关键步骤。
#### 算法核心代码
```matlab
function [bestSolution, bestCost] = SimulatedAnnealingCostFunction(costFunction, initialSolution, temperatureSchedule)
% 模拟退火算法实现
% 初始化参数
currentSolution = initialSolution;
currentCost = costFunction(currentSolution);
bestSolution = currentSolution;
bestCost = currentCost;
T = temperatureSchedule.initialTemperature;
% 算法主循环
while T > temperatureSchedule.finalTemperature
for i = 1:temperatureSchedule.innerIterations
% 产生新解
newSolution = perturbSolution(currentSolution);
newCost = costFunction(newSolution);
% 接受准则
if acceptNewSolution(currentCost, newCost, T)
currentSolution = newSolution;
currentCost = newCost;
end
% 更新最佳解
if newCost < bestCost
bestSolution = newSolution;
bestCost = newCost;
end
end
T = decreaseTemperature(T);
end
end
function newSolution = perturbSolution(solution)
% 产生新解的函数
% 此处省略具体实现细节
end
function decision = acceptNewSolution(cost, newCost, temperature)
% 接受新解的准则函数
% 此处省略具体实现细节
end
function newTemperature = decreaseTemperature(temperature)
% 降温函数
% 此处省略具体实现细节
end
```
#### 参数说明与优化
在上述代码中,`costFunction`是一个用户定义的函数,用于计算解的成本或适应度。`initialSolution`是初始解,`temperatureSchedule`是一个结构体,定义了温度的初始值、最终值以及内循环次数。
- `initialTemperature`:初始温度,高初始温度有助于在搜索空间中进行广泛的探索。
- `finalTemperature`:最终温度,当温度降至此值以下时,算法停止。
- `innerIterations`:内循环的迭代次数,每次温度下降都会执行一定次数的迭代。
在优化这部分代码时,需要根据具体问题调整`perturbSolution`、`acceptNewSolution`和`decreaseTemperature`函数的实现。例如,在`perturbSolution`函数中,可以采用不同的扰动策略来生成新解,如交换、插入或逆转序列中的元素等。
在`acceptNewSolution`函数中,通常使用Metropolis准则来决定是否接受新解:
```matlab
function decision = acceptNewSolution(cost, newCost, temperature)
if newCost < cost
decision = true;
else
probability = exp((cost - newCost) / temperature);
decision = rand() < probability;
end
end
```
### 实际案例与操作步骤
为了更深入地理解MATLAB中模拟退火算法的实现,这里给出一个简单的案例——旅行商问题(TSP)的求解。
#### 旅行商问题(TSP)
旅行商问题是一个经典的优化问题,要求找出一条最短的路径,访问一系列城市并返回起点。
#### 操作步骤
1. 定义成本函数:计算旅行路径的总长度。
2. 初始解:随机生成一个路径作为初始解。
3. 设置温度计划:例如,初始温度设为路径总长度的10%,最终温度为0.001,内循环次数设为100。
4. 运行模拟退火算法:调用前面定义的`SimulatedAnnealingCostFunction`函数求解TSP。
通过调整算法参数和实现细节,MATLAB能够成为研究和解决各类优化问题的有效工具。模拟退火算法的实现不仅适用于理论研究,更能在实际工程应用中解决诸多复杂问题。
以上是在MATLAB环境下搭建模拟退火算法开发环境及实现基础框架的过程。下一章节将深入探讨模拟退火算法的理论背景及其在工程优化问题中的具体应用。
# 3. 模拟退火算法的理论与实践
## 模拟退火算法概述
模拟退火算法(Simulated Annealing, SA)是一种通用概率算法,用来在一个大的搜寻空间内寻找足够好的解。它是由S. Kirkpatrick、C. D. Gelatt和M. P. Vecchi在1983年提出的。该算法的灵感来源于固体物质退火过程,特别是物理冶金学中提到的退火现象。通过逐渐减低温度并允许系统达到热平衡,一个固体物质的原子重新排列,最小化系统的能量。类似地,模拟退火算法逐渐降低“温度”(系统能量的代表),通过概率性的接受准则,引导搜索过程跳出局部最优,进而寻找到全局最优解。
## 算法原理
模拟退火算法的核心在于“接受准则”,该准则由Metropolis准则衍生而来,公式表示如下:
\[ P(e_i \rightarrow e_j) = \left\{
\begin{array}{ll}
1 & \text{if } \Delta E > 0 \\
e^{\frac{\Delta E}{T}} & \text{if } \Delta E \leq 0
\end{array}
\right. \]
其中,\(e_i\) 和 \(e_j\) 代表系统当前状态与新状态,\(\Delta E\) 是两者之间的能量差,\(T\) 是当前系统的“温度”。当新状态的能量较低时(\(\Delta E > 0\)),新状态总被接受;如果能量较高(\(\Delta E \leq 0\)),新状态以一定的概率被接受,这概率随着温度的降低而降低。这个准则允许算法在搜索初期接受劣质解,避免陷入局部最小值,增加了达到全局最优解的机会。
### 算法流程
模拟退火算法主要包括初始化、解的产生和评价、接受准则判断、冷却过程四个步骤:
1. **初始化**:设置初始温度\(T\),最高温度\(T_{max}\),最低温度\(T_{min}\),冷却率\(\alpha\)等参数,并选择一个初始解。
2. **解的产生和评价**:在当前解的邻域中随机选择一个新的解,并计算与当前解的能量差。
3. **接受准则判断**:根据Metropolis准则判断新解是否被接受,并更新当前解。
4. **冷却过程**:按照预定的冷却计划降低系统温度,并决定是否继续迭代。
```mermaid
graph TD;
A[开始] --> B[设置初始温度T]
B --> C[选择初始解]
C --> D[产生新解]
D --> E{能量差ΔE}
E -- ΔE ≤ 0 --> F[按Metropolis准则接受新解]
E -- ΔE > 0 --> G[100%接受新解]
F --> H[降低温
```
0
0





