【排序算法深入】：LeetCode中各种排序算法的应用场景


# 摘要
排序算法是计算机科学中不可或缺的基础组成部分，它们在数据处理和存储方面发挥着核心作用。本文首先介绍了排序算法的基础知识，并详细探讨了冒泡排序、快速排序和归并排序等常见排序算法的原理及代码实现。接着，文章分析了各种排序算法的时间复杂度和空间复杂度，包括在最好、最坏和平均情况下的表现。在此基础上，文中进一步探讨了排序算法在实际面试及实际项目中的应用，如在大数据场景下的排序策略以及与其他算法结合的性能影响。通过深入剖析这些算法，本文旨在为读者提供一个全面了解排序算法及其实际应用的视角。

# 关键字
排序算法；时间复杂度；空间复杂度；大数据排序；算法优化；性能分析

参考资源链接：[LeetCode中文版算法详解：从入门到精通必备](https://wenku.csdn.net/doc/6412b6dbbe7fbd1778d48391?spm=1055.2635.3001.10343)
# 1. 排序算法的基础知识

在计算机科学与编程领域，排序算法是基础且至关重要的算法之一。排序算法的作用是对一系列元素按照特定的顺序（通常是从小到大或者从大到小）进行排列。正确理解和掌握排序算法不仅对解决实际问题有帮助，而且在面试和工作中也是衡量一个程序员基本功的重要标准。排序算法的效率通常通过时间复杂度和空间复杂度来衡量，而对于特定的应用场景，选择合适的排序算法也至关重要。本章将介绍排序算法的基本概念和分类，为后续章节深入探讨各类排序算法打下坚实的理论基础。

# 2. 常见的排序算法及其实现

## 2.1 冒泡排序算法

### 2.1.1 冒泡排序的原理

冒泡排序是一种简单的排序算法，它重复地走访过要排序的数列，一次比较两个元素，如果他们的顺序错误就把他们交换过来。走访数列的工作是重复地进行直到没有再需要交换，也就是说该数列已经排序完成。这个算法的名字由来是因为越小的元素会经由交换慢慢“浮”到数列的顶端。

从算法实现的角度来看，冒泡排序的工作原理是通过重复遍历待排序的列表，比较相邻元素，如果前一个比后一个大，就交换他们的位置。每一轮遍历都会确保列表的最大元素“冒泡”到正确的位置，对于 n 个元素，需要 n-1 轮遍历。

### 2.1.2 冒泡排序的代码实现

def bubble_sort(arr):
    n = len(arr)
    for i in range(n):
        # 假设这个列表已经排好序了
        already_sorted = True
        # 每轮遍历都将最大的数“冒泡”到正确的位置
        for j in range(n - i - 1):
            if arr[j] > arr[j + 1]:
                # 交换元素
                arr[j], arr[j + 1] = arr[j + 1], arr[j]
                already_sorted = False
        # 如果这一轮没有发生任何交换，说明列表已经排序完成
        if already_sorted:
            break
    return arr

在上面的 Python 代码中，`bubble_sort` 函数对列表 `arr` 进行排序。外层循环控制遍历的轮数，内层循环负责进行相邻元素的比较和必要的交换。变量 `already_sorted` 用来检查在某一轮遍历中是否发生了交换操作，如果没有交换发生，则说明列表已经是排序好的，可以提前终止算法。

## 2.2 快速排序算法

### 2.2.1 快速排序的原理

快速排序是目前被认为最快的排序算法之一。它的基本思想是通过一趟排序将待排记录分隔成独立的两部分，其中一部分记录的关键字均比另一部分的关键字小，则可分别对这两部分记录继续进行排序，以达到整个序列有序。

快速排序使用分治策略来把一个序列分为较小和较大的两个子序列，然后递归地排序两个子序列。具体的分割操作是，选取一个元素作为"基准"（pivot），重新排列列表，所有比基准值小的元素摆放在基准前面，所有比基准值大的元素摆放在基准后面（相同的数可以到任一边）。在这个分区退出之后，该基准就处于数列的中间位置，这个称为分区（partition）操作。递归地（recursive）把小于基准值元素的子序列和大于基准值元素的子序列排序。

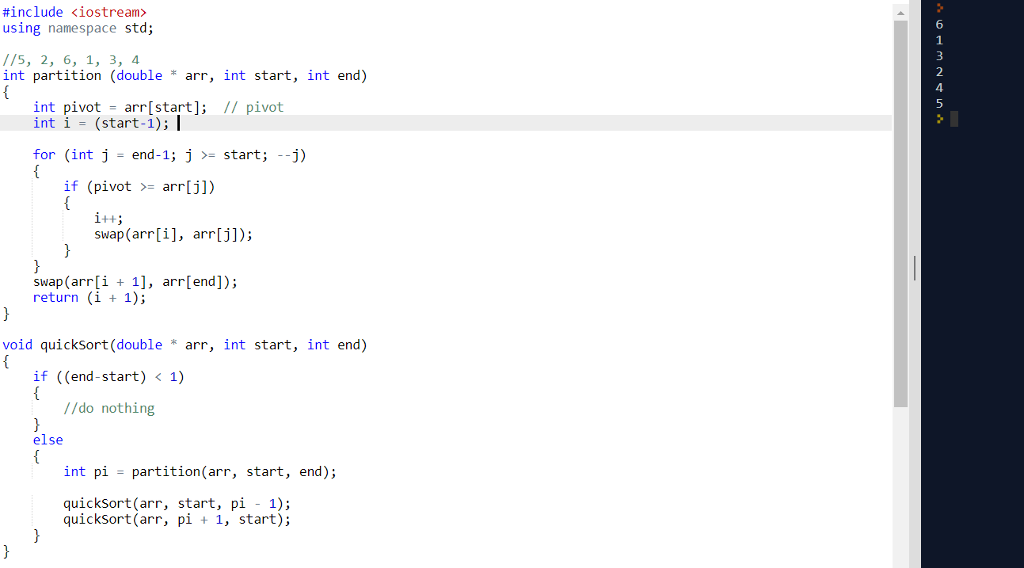
### 2.2.2 快速排序的代码实现

def quick_sort(arr):
    if len(arr) <= 1:
        return arr
    else:
        pivot = arr[0]
        less = [x for x in arr[1:] if x <= pivot]
        greater = [x for x in arr[1:] if x > pivot]
        return quick_sort(less) + [pivot] + quick_sort(greater)

上述 Python 代码通过递归实现快速排序算法。首先，如果数组只有一个元素或为空，那么它已经有序，直接返回。接着，选取列表的第一个元素作为基准，创建两个新列表 `less` 和 `greater`，分别包含小于和大于基准值的元素。最后，递归地对这两个列表进行排序，然后将结果与基准值连接起来，形成最终排序后的列表。

## 2.3 归并排序算法

### 2.3.1 归并排序的原理

归并排序是建立在归并操作上的一种有效的排序算法。该算法是采用分治法的一个非常典型的应用。即将两个或两个以上的有序表合并成一个新的有序表，即把待排序序列分为若干个子序列，每个子序列是有序的。然后再把有序子序列合并为整体有序序列。

归并排序过程主要分为两个步骤：分解（Divide）和合并（Conquer）。分解就是递归地将当前区间一分为二，直到每个子区间只有一个位置，而合并则是将两个已经有序的子序列合并成一个有序序列。

归并操作是合并排序中，用于合并两个已排序数组为一个有序数组的算法。具体步骤如下：

1. 申请空间，使其大小为两个已经排序序列之和，该空间用来存放合并后的序列。
2. 设定两个指针，最初位置分别为两个已经排序序列的起始位置。
3. 比较两个指针所指向的元素，选择相对小的元素放入到合并空间，并移动指针到下一位置。
4. 重复步骤3直到某一指针到达序列尾。
5. 将另一序列剩下的所有元素直接复制到合并序列尾。

### 2.3.2 归并排序的代码实现

def merge_sort(arr):
    if len(arr) > 1:
        mid = len(arr) // 2
        L = arr[:mid]
        R = arr[mid:]

        # 递归地对两个子列表进行排序
        merge_sort(L)
        merge_sort(R)

        i = j = k = 0

        # 合并两个有序的子列表
        while i < len(L) and j < len(R):
            if L[i] < R[j]:
                arr[k] = L[i]
                i += 1
            else:
                arr[k] = R[j]
                j += 1
            k += 1

        # 将剩余的元素复制到原列表
        while i < len(L):
            arr[k] = L[i]
            i += 1
            k += 1

        while j < len(R):
            arr[k] = R[j]
            j += 1
            k += 1
    return arr

上述 Python 代码实现了归并排序算法。首先，检查列表的