控制系统设计实战：根轨迹法中的幅值和相角，专家级优化技巧


# 摘要
本文全面介绍了控制系统设计中根轨迹法的理论基础、实践应用以及优化技巧。首先概述了控制系统设计的重要性，接着详细阐述了根轨迹法的基本原理和绘制步骤，并介绍了如何通过幅值和相角条件进行系统稳定性分析。第三章深入探讨了根轨迹分析的软件工具使用和系统性能评估，以及根轨迹法在控制系统设计中的具体应用案例。第四章则侧重于系统优化技巧，包括专家级系统优化概念、根轨迹法的幅值和相角优化，以及实际优化案例分析。最后一章讨论了非线性系统和多变量系统的根轨迹分析，以及根轨迹法与其他设计方法的融合，并对控制系统设计的未来趋势进行了展望。

# 关键字
控制系统设计；根轨迹法；系统稳定性；软件工具；系统性能评估；优化技巧；非线性系统；多变量系统

参考资源链接：[根轨迹法解析：幅值条件与相角条件的几何意义](https://wenku.csdn.net/doc/58mis5o7sb?spm=1055.2635.3001.10343)
# 1. 控制系统设计概述

控制系统设计是工程实践中的重要环节，它涉及到如何使一个物理系统按照预定的方式运行。本章将概述控制系统设计的基本理念与方法，为后续章节中深入讨论控制系统设计的具体技术，例如根轨迹法，打下坚实的基础。

## 1.1 控制系统设计的目的和原则

控制系统设计的目的是使被控制对象能够根据特定的输入，达到或维持期望的输出状态。设计原则强调系统要具备稳定性、快速性和准确性等核心特性。为了实现这些特性，控制系统设计师需要综合运用数学建模、仿真分析、参数优化等多种工具和方法。

## 1.2 控制系统设计的基本步骤

控制系统设计通常遵循以下步骤：
1. 需求分析：明确系统性能指标，包括稳态误差、响应速度、稳定性等要求。
2. 系统建模：将物理系统抽象为数学模型，如传递函数或状态空间模型。
3. 分析与设计：利用根轨迹法等工具，分析系统特性，并设计控制器。
4. 模拟仿真：在软件环境中测试和验证控制器性能。
5. 硬件实现：将控制算法实现在实际的物理装置中。
6. 调试优化：根据现场测试结果，调整和优化控制器参数。

通过这些步骤，设计者可以确保系统的可靠性和满足设计要求，为实现复杂的控制任务奠定基础。在后续章节中，我们将重点深入探讨根轨迹法，它是控制系统设计中一种强大的分析和设计工具。

# 2. 根轨迹法理论基础

根轨迹法是控制系统设计中一种强大的工具，它帮助工程师理解和设计控制系统的稳定性和性能。在这一章中，我们将深入探讨根轨迹法的理论基础，包括其原理、幅值和相角条件，以及扩展应用。

### 2.1 根轨迹法原理

#### 2.1.1 根轨迹定义与特性

根轨迹技术是由W.R. Evans在1948年首次提出的，它是一种图形化方法，用于分析和设计闭环控制系统的稳定性和性能。通过根轨迹图，工程师可以看到系统特征方程的根如何随着某个系统参数（通常是增益）的变化而变化。

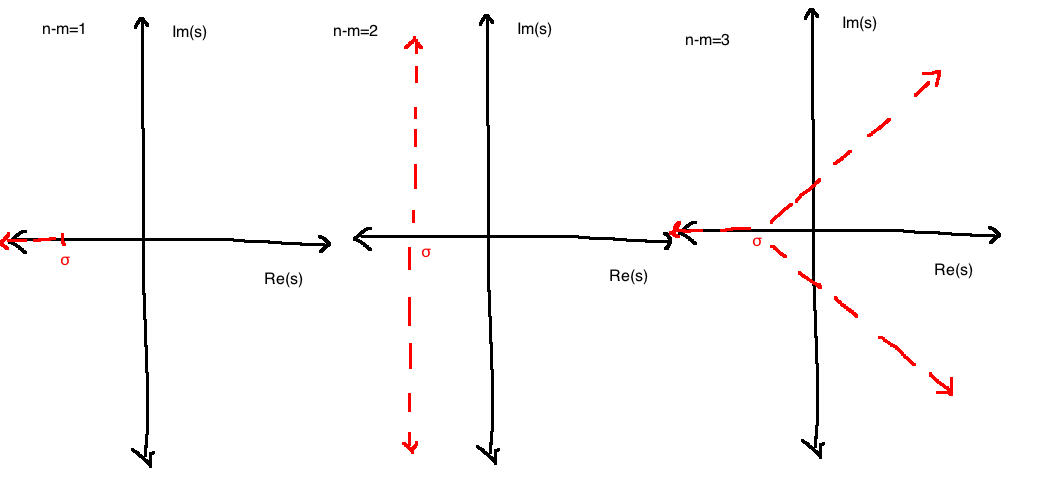
根轨迹图是复平面上的一系列轨迹，代表了系统开环传递函数的极点随开环增益变化时的运动路径。每条轨迹开始于开环极点，结束于开环零点或者无穷远处，且满足角度条件和幅值条件。

**根轨迹的特性包括：**

- 根轨迹在复平面上的分支数等于开环传递函数的极点数。
- 根轨迹的起点为开环传递函数的极点，终点为零点，若零点数量少于极点，则部分根轨迹趋向无穷远。
- 根轨迹在实轴上的分布，必须位于奇数个极点和零点的左侧。
- 根轨迹的分支在进入复平面右半部分之前，必定与实轴上的某点相交。

#### 2.1.2 根轨迹的绘制步骤

绘制根轨迹的步骤通常包括：

1. 确定开环传递函数的极点和零点。
2. 计算根轨迹的分支数（开环极点数）。
3. 标出根轨迹在实轴上的分布。
4. 计算根轨迹的渐近线（如果存在）。
5. 利用角度条件计算根轨迹的交点和终点。
6. 计算特定增益值时的根轨迹点。

在绘制根轨迹时，可以使用各种工具，如MATLAB或Python的控制系统工具箱来辅助计算和可视化。

### 2.2 根轨迹法的幅值和相角条件

根轨迹法不仅提供根轨迹图形，还根据幅值和相角条件来保证系统的稳定性和性能。

#### 2.2.1 幅值条件与增益计算

幅值条件指出了在复平面上的某个点要成为根轨迹上一点，必须满足开环增益K的幅值条件。该条件可以通过开环传递函数在该点的增益来计算，用公式表示为：

\[ |G(s)H(s)| = \frac{1}{K} \]

其中，\( G(s) \) 是开环传递函数的分子部分，\( H(s) \) 是分母部分，\( K \) 是增益，\( s \) 是拉普拉斯变换中的复变量。

#### 2.2.2 相角条件与稳定性分析

相角条件则用于检查根轨迹上某点的相位角是否满足闭环系统稳定的条件。闭环稳定性要求所有特征根均位于复平面左半部分，这意味着它们的相角必须为负。因此，可以通过计算根轨迹上某点的相角来判断系统的稳定性。

### 2.3 根轨迹法的扩展应用

根轨迹法的理论基础不仅适用于简单的单变量系统，还可以扩展到更复杂的系统设计中。

#### 2.3.1 广义根轨迹的定义

广义根轨迹的概念扩展了传统根轨迹的概念，不仅包括了开环增益的变化，还可以是其他参数的变化。例如，在具有时变参数的系统中，可以研究这些参数变化对系统根的影响。

#### 2.3.2 广义根轨迹的绘制和分析

绘制广义根轨迹的过程更为复杂，因为涉及多个参数的变化。在多参数的系统中，可以使用软件工具如MATLAB的控制系统工具箱中的`rlocus`函数来进行绘制，但需要对函数进行适当的修改以适应广义根轨迹的计算。

**使用MATLAB绘制广义根轨迹的代码示例：**

num = [3 2]; % 分子多项式系数
den = [1 7 12]; % 分母多项式系数
sys = tf(num, den); % 创建传递函数模型

K_range = [0:0.1:10]; % 定义增益范围
rlocus(sys, K_range); % 绘制根轨迹
title('广义根轨迹图');
grid on;

通过上述MATLAB代码，我们可以绘制出一个给定传递函数模型的广义根轨迹图。其中，`K_range`定义了增益的变化范围，而`rlocus`函数则负责绘制出根轨迹。

在本节中，我们对根轨迹法的理论基础进行了深入探讨，包括其定义、绘制步骤、幅值和相角条件以及广义根轨迹的概念和扩展应用。接下来，我们将在第三章中探讨根轨迹法在实践应用中的具体案例和分析方法。

# 3. 根轨迹法实践应用

## 3.1 根轨迹分析的软件工具

根轨迹法是控制系统设计中重要的分析工具，而借助计算机软件工具可以更加直观和高效地进行根轨迹分析。在众多的软件工具中，MATLAB因为其强大的数学计算能力和丰富的工具箱支持，成为了工程师进行控制系统分析的首选工具。

### 3.1.1 使用MATLAB绘制根轨迹

MATLAB提供了一个专门用于绘制根轨迹的函数——`rlocus`，这个函数可以轻松地绘制出线性时不变系统的根轨迹图。使用`rlocus`函数的基本格式如下：

sys = tf(num, den); % 创建传递函数模型
rlocus(sys); % 绘制根轨迹图

在上述代码中，`num` 和 `den` 分别代表系统的分子和分母多项式系数。执行`rlocus(sys)`后，MATLAB会显示出系统的根轨迹图。

例如，我