设计优化深度案例:Pumplinx仿真在外啮合齿轮泵中的应用探究
发布时间: 2024-12-18 23:20:28 订阅数: 2 


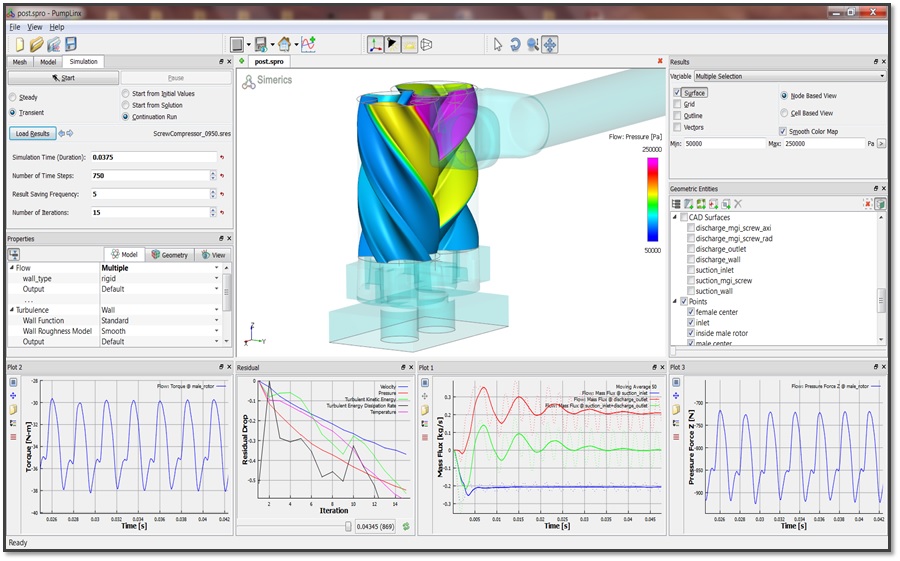
Pumplinx外啮合齿轮泵仿真教程
# 摘要
本文首先介绍了外啮合齿轮泵的工作原理和设计基础,然后详细探讨了Pumplinx仿真软件的功能、理论基础以及操作流程。文章进一步阐述了Pumplinx在齿轮泵设计优化中的具体应用,包括设计参数优化、效率提升以及故障分析。通过实际案例分析,本文展示了Pumplinx在提升齿轮泵性能方面的有效性,并对优化结果进行了评估。最后,本文展望了Pumplinx仿真技术的未来发展趋势与挑战,包括技术进步、行业应用前景以及面临的主要挑战和应对策略。
# 关键字
外啮合齿轮泵;Pumplinx仿真;设计优化;流量分析;多物理场耦合;故障分析
参考资源链接:[Simerics mp+ Pumplinx齿轮泵仿真教程:Solidworks流体域提取](https://wenku.csdn.net/doc/5hrc688sk8?spm=1055.2635.3001.10343)
# 1. 外啮合齿轮泵的工作原理与设计基础
## 1.1 工作原理概述
外啮合齿轮泵是一种常见的液压传动元件,其工作原理是利用两个相互啮合的齿轮在泵壳内转动产生容积变化来输送液体。齿轮转动时,它们之间以及齿轮与泵壳之间形成的空间在吸入端逐渐增大,产生负压吸入液体,而在排出端逐渐减小,将液体挤压出去。
## 1.2 设计中的基础考量
设计外啮合齿轮泵时,需要综合考虑多种因素。首先是泵的流量和压力,这两个参数决定了泵的总体尺寸和齿轮的几何参数。其次是材料选择,泵壳和齿轮需要耐磨损、抗腐蚀且具备良好的机械强度。此外,齿轮泵的效率、噪声、振动和寿命也是设计时必须考虑的重要因素。
## 1.3 关键设计参数的确定
精确设计外啮合齿轮泵的关键在于确定合适的齿轮参数,包括模数、齿数、压力角等。模数和齿数决定了齿轮的尺寸,而压力角影响齿轮的啮合效率和强度。泵壳的设计需要确保适当的间隙,以便齿轮能够顺畅地旋转,同时也要最小化液体泄漏。这些参数的综合考虑对实现高效、可靠和经济的齿轮泵设计至关重要。
# 2. Pumplinx仿真软件介绍
## 2.1 Pumplinx软件概述
### 2.1.1 软件功能与界面布局
Pumplinx是一款先进的流体动力学仿真软件,它集成了多种复杂的仿真算法和工具,用于模拟液压系统和组件的动态行为。该软件能够模拟流体在液压系统中的流动情况,并预测系统在各种运行条件下的性能表现。Pumplinx的界面布局经过精心设计,确保用户能以直观和高效的方式完成复杂的仿真任务。主界面通常由几个主要部分组成:项目管理、模型构建、边界条件设置、求解器控制以及结果分析等模块。
通过这个布局,工程师可以轻松地进行模型的创建、编辑,设置仿真的参数,运行仿真,并分析仿真结果。Pumplinx还提供了一系列的辅助工具,比如数据库管理、材料属性数据库和预定义的仿真模板,使得用户能够快速上手并优化他们的设计。
### 2.1.2 Pumplinx在流体仿真中的优势
Pumplinx相较于其他流体仿真软件,具有以下几个显著的优势:
1. 高效的网格生成器:Pumplinx内置的网格生成器能够快速地生成高质量的多面体网格,这对于精确模拟流体动力学行为至关重要。
2. 多物理场耦合:能够同时考虑流体流动、热传递、固体结构变形等多个物理场的相互作用。
3. 高级求解技术:Pumplinx采用了最新的数值求解技术,可以处理高度非线性问题,以及在极端工况下的流动模拟。
4. 定制化和可扩展性:软件的开放架构允许用户自定义模型和材料属性,满足特定行业和应用的需要。
## 2.2 Pumplinx仿真的理论基础
### 2.2.1 流体力学的数学模型
在流体力学中,Navier-Stokes方程是描述流体运动的基础方程。这组方程在数学上描述了流体的速度场、压强场以及其他热力学参数如何随时间和位置变化。在Pumplinx中,通过数值方法(如有限元分析或有限体积法)将这些偏微分方程离散化,用于计算机模拟。以下是一些基本的数学模型:
- 连续性方程(质量守恒):
\[
\frac{\partial \rho}{\partial t} + \nabla \cdot (\rho \mathbf{v}) = 0
\]
- 动量方程(动量守恒):
\[
\frac{\partial (\rho \mathbf{v})}{\partial t} + \nabla \cdot (\rho \mathbf{v} \mathbf{v}) = -\nabla p + \nabla \cdot \mathbf{T} + \mathbf{f}
\]
- 能量方程(能量守恒):
\[
\frac{\partial (\rho E)}{\partial t} + \nabla \cdot (\rho \mathbf{v} E) = -\nabla \cdot \mathbf{q} + \nabla \cdot (\mathbf{v} \cdot \mathbf{T}) + \rho \mathbf{f} \cdot \mathbf{v}
\]
在以上方程中,\( \rho \) 是流体密度,\( \mathbf{v} \) 是流体速度矢量,\( p \) 是压强,\( \mathbf{T} \) 是应力张量,\( \mathbf{f} \) 是体积力(如重力),\( \mathbf{q} \) 是热通量,\( E \) 是单位体积的总能量。
### 2.2.2 仿真模型的建立与验证
仿真模型的建立是使用Pumplinx进行仿真分析的第一步,通常包括以下步骤:
1. 模型几何的构建:基于实际应用创建几何模型,这可以通过CAD软件完成,然后导入Pumplinx。
2. 网格划分:将几何模型划分为有限的网格单元,Pumplinx提供自动化的网格生成器,可以适应各种复杂性级别的几何。
3. 物理边界条件的设定:定义流体的入口、出口边界条件,以及可能存在的固体表面的滑移或粘附条件等。
4. 材料属性和流体属性的指定:包括密度、粘度、热导率、比热容等。
5. 求解器的选择:根据问题的类型和需求选择合适的求解器,例如隐式或显式求解器、压力或速度求解器。
仿真模型的验证是确保仿真的结果准确的关键步骤。这通常涉及以下操作:
1. 网格无关性检验:通过增加网格的精度来检查结果的变化,确保结果不会因网格的细化而显著改变。
2. 结果对比分析:将仿真结果与实验数据或其他已验证的仿真结果进行对比。
3. 敏感性分析:对模型的关键参数进行变参分析,以判断参数的不确定性对结果的影响。
## 2.3 Pumplinx仿真的操作流程
### 2.3.1 前处理:模型构建与材料定义
前处理是进行仿真分析的重要阶段。在Pumplinx中,模型构建和材料定义是完成前处理的关键步骤:
#### 模型构建
- **几何模型导入**:首先,需要从CAD软件导出几何模型文件(如STEP或IGES格式),然后在Pumplinx中导入。
- **几何清理**:检查导入的几何模型是否有错误或重叠部分,使用Pumplinx提供的工具进行必要的修正。
- **简化和抽取**:如果模型过于复杂,可能需要简化或抽取关键特征来减小计算量。
#### 材料定义
- **选择材料库**:Pumplinx提供了一个广泛的材料库,包含多种流体和固体材料的属性数据。
- **创建自定义材料**:如果预定义材料库中没有所需的材料,可以创建一个自定义材料并输入其属性数据。
- **属性设置**:为固体部件指定材料属性(如密度、弹性模量、泊松比等),为流体指定密度、粘度以及其他可能的热物理性质。
### 2.3.2 中处理:边界条件与求解器设置
在仿真模型建立和材料属性定义之后,接下来进行边界条件的设置和求解器的配置。
#### 边界条件设置
- **定义流体域**:标识出模型中的流体区域,这是求解流动问题的基础。
- **设置边界条件**:包括速度入口、压力出口、壁面条件等,这些条件将直接影响流体的流动和性能。
- **初始化条件**:给定初始的流场参数,如速度、压强、温度分布等。
#### 求解器配置
- **选择求解器类型**:根据问题的性质,选择合适的求解器。例如,对于不可压缩流体,可以使用压力基求解器;对于可压缩流体,则可能使用密度基求解器。
- **定义求解策略**:设置求解的收敛标准,比如残差水平、迭代步数等。
- **
0
0





