【Chan算法精度评估】：提升算法准确性的关键方法


# 摘要
本文综述了算法精度评估的基础知识，并对Chan算法的理论基础、实现、优化和实证分析进行了深入探讨。首先介绍了Chan算法的历史背景、核心数学模型和假设条件，并详细分析了算法的实现步骤。接着，通过实证分析与案例研究，本文探讨了数据预处理、性能评估指标、具体应用场景下的算法应用及其效果评估。随后，文章着重阐述了提升Chan算法精度的多种策略，包括数据层面和算法层面的优化方法以及后处理技术的应用。最后，展望了Chan算法未来的发展趋势，包括新兴技术的融合、算法鲁棒性评估和评估方法创新与标准化。本文为研究和应用Chan算法提供了全面的理论支持与实践指导。

# 关键字
算法精度评估；Chan算法；性能指标；数据预处理；模型优化；未来趋势

参考资源链接：[MATLAB实现：Chan算法解决TDOA定位](https://wenku.csdn.net/doc/6s6ken703n?spm=1055.2635.3001.10343)
# 1. 算法精度评估概述

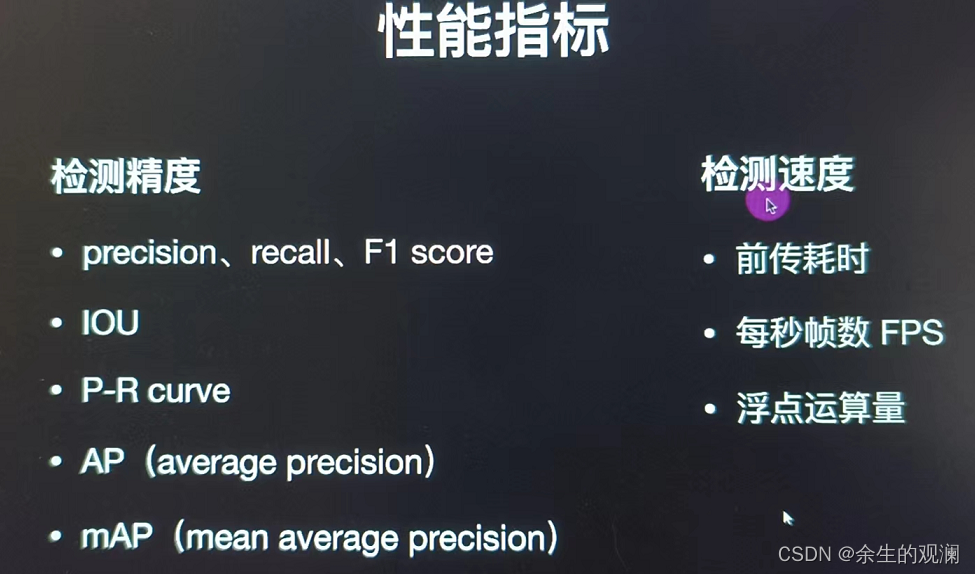
算法精度评估是衡量算法性能和可靠性的重要环节，尤其是在数据科学和机器学习领域。本章将概述精度评估的基本概念、重要性以及常规方法。我们将从算法性能评估的必要性讲起，阐明为何评估是算法开发不可或缺的一部分。随后，我们会探索不同的性能指标，如精确度、召回率和F1分数，它们如何为算法性能提供全面的视角。本章内容将为读者打下扎实的基础，为进一步深入学习Chan算法的理论与实践做好准备。

# 2. Chan算法的理论基础与实现

### 2.1 Chan算法的原理

#### 2.1.1 算法的历史背景和发展

Chan算法，作为一种经典的信号处理技术，最初由Wai-Kai Chan于20世纪末提出。在当时，该算法主要应用于数字信号处理领域，尤其在图像去噪和边缘保持方面表现出色。随着时间的推移，Chan算法经历了多次迭代和发展，尤其在计算机视觉和模式识别领域中，其应用得到了显著拓展。

算法的发展与多学科领域的交叉融合密切相关，例如统计学、机器学习和最优化理论。随着计算能力的提升，Chan算法能够处理更大规模的数据集，其应用范围也从单纯的图像处理扩展到了更为广泛的信号分析领域。随着深度学习的兴起，Chan算法与现代人工智能技术的融合也成为了研究热点之一。

#### 2.1.2 核心数学模型和假设条件

Chan算法的核心在于其数学模型，它通常基于线性代数和概率论。算法的基本假设条件是信号可以通过某个数学模型表达，且噪声与信号是独立的。在处理图像时，Chan算法假设图像的边缘可以由线性或非线性模型表示，并且图像的局部区域在像素上是平滑的。

数学上，Chan算法往往涉及到最小化一个特定的代价函数，该函数结合了数据保真项和正则化项。数据保真项用于描述信号与观测数据的匹配程度，而正则化项则用于引导解的光滑性或稀疏性。通过求解这样一个优化问题，算法能够得到一个既符合数据观测又在某种意义上的最优估计。

### 2.2 Chan算法的参数设置与优化

#### 2.2.1 参数设定的影响因素

Chan算法的性能受到多个参数的影响，这些参数的选择往往基于具体应用场景和数据集的特性。主要的参数包括正则化强度、迭代次数、以及用于平滑的邻域大小等。参数设置不当会导致算法过拟合或欠拟合，影响最终的处理结果。

正则化强度是控制算法保真度与平滑性之间平衡的关键因素。一个较小的正则化参数可能会使得算法过于强调数据的拟合，从而忽略了图像或信号的平滑性，导致噪声的放大。反之，一个过大的正则化参数可能会过度平滑信号，丢失重要特征。因此，选择合适的正则化参数对于算法性能至关重要。

#### 2.2.2 参数优化的方法和策略

参数优化是一个挑战性的任务，因为它需要在保真度和平滑性之间找到最佳平衡点。一种常用的策略是利用交叉验证来评估不同参数设置下的性能。通过选取部分数据进行训练，其他部分数据进行验证，可以有效地估计算法在未知数据上的表现。

此外，可以使用梯度下降、牛顿法等优化算法进行参数的自适应调整。在一些高级的应用中，采用贝叶斯优化和遗传算法等更复杂的方法可以进一步提升参数的优化效果。这些方法能够在全局搜索空间中寻找最佳参数，避免陷入局部最优解。

### 2.3 Chan算法的步骤分解

#### 2.3.1 算法流程的详细步骤

Chan算法的实现通常包括以下步骤：
1. 初始化参数：设置正则化强度、迭代次数等。
2. 建立代价函数：结合数据保真项和正则化项。
3. 迭代优化：通过迭代求解器逐步更新解，直至收敛。
4. 结果输出：输出去噪后的信号或图像。

初始化参数是整个算法流程的起点。在实践中，参数的设置通常基于经验规则或者通过实验确定。建立代价函数是算法的核心部分，其设计直接影响到算法的性能。

迭代优化过程是算法中最为复杂和计算密集的步骤。在每一步迭代中，需要利用诸如共轭梯度法、梯度下降等优化算法来求解代价函数的最小值。最终，算法通过多次迭代得到的解即为去噪或平滑后的结果。

#### 2.3.2 关键步骤的深入分析

在Chan算法的迭代优化步骤中，关键在于优化算法的选择和实施。例如，共轭梯度法是一种有效的迭代优化方法，它利用了Hessian矩阵的信息来加速收敛。共轭梯度法特别适合大规模稀疏系统，可以显著减少内存使用，并提高计算速度。

下面展示一个简化的Chan算法的伪代码实现，用于说明算法的基本结构：

# 初始化参数
alpha = 0.1 # 正则化强度
max_iter = 100 # 最大迭代次数

# 建立代价函数
def cost_function(signal, estimated_signal):
    # 计算数据保真项和正则化项的组合
    pass

# 迭代优化过程
def optimize(estimated_signal):
    for i in range(max_iter):
        # 计算梯度
        gradient = compute_gradient(estimated_signal)
        # 更新估计信号
        estimated_signal = update_estimate(estimated_signal, gradient)
        # 检查收敛性
        if is_converged(gradient):
            break
    return estimated_signal

# 主程序
initial_estimate = initialize_signal()
final_estimate = optimize(initial_estimate)

在此伪代码中，`compute_gradient`和`update_estimate`需要根据具体的数学模型来具体实现。`is_converged`函数用于评估算法是否已经收敛，可能是基于梯度大小的阈值判断，或者是连续迭代解的变化量。

在实际应用中，Chan算法的每一步都需要