【线程安全的最佳实践】：利用java.time中的不可变对象

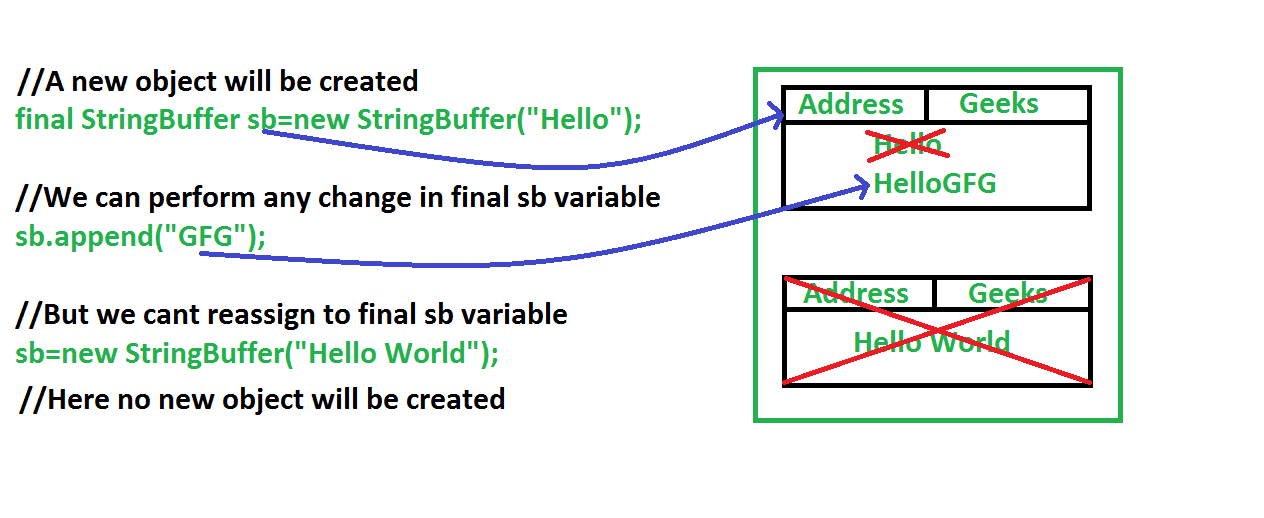
# 1. 理解线程安全的重要性

在多线程编程中，线程安全是一个核心概念。线程安全问题通常发生在多个线程同时访问和修改共享资源时，可能导致数据不一致或竞态条件。理解线程安全的重要性有助于我们设计出健壮的并发应用程序。具体来说：

## 1.1 线程安全概念

线程安全意味着当多个线程访问某个类时，这个类始终能表现出正确的行为。为实现线程安全，需要确保共享资源的访问是同步的，或者是不可变的。

## 1.2 线程安全的影响

不当的线程安全处理会导致数据损坏、应用崩溃，甚至系统安全问题。线程安全的代码维护难度大，性能也可能受到影响。

## 1.3 实现线程安全的方法

实现线程安全可以通过多种方式，包括使用同步机制、锁、或者采用无锁编程技术。其中，利用不可变对象是实现线程安全的一个有效手段，我们将通过接下来的章节详细介绍。

# 2. Java中的不可变对象

### 2.1 不可变对象的定义和特性

#### 2.1.1 不可变性的定义

不可变对象是一个一旦创建就不能被修改的对象。在Java中，不可变对象的所有字段都是最终的(final)，这意味着一旦对象被实例化，它的状态就不能再改变。不可变对象的优点之一是它们是线程安全的，因为多个线程可以安全地共享一个不可变对象的引用，而无需担心并发修改问题。尽管创建不可变对象可能会产生额外的性能成本，比如创建对象的副本，但它们带来的好处通常超过了这些成本。

#### 2.1.2 不可变对象的好处

1. **线程安全**：由于不可变对象的状态在创建后就不能改变，所以它们天然就是线程安全的，无需额外的同步措施。
2. **易于理解和维护**：不可变对象的状态永远不会改变，这使得它们的行为更容易预测，且更易于在复杂的系统中进行推理和测试。
3. **安全性**：在多线程环境中，不可变对象提供了一种避免并发修改异常的安全方式。
4. **高效的缓存**：由于不可变对象的状态不会改变，它们可以被自由地缓存和重用，这在某些情况下可以提高性能。

### 2.2 Java中的不可变类设计

#### 2.2.1 final关键字的作用

在Java中，`final`关键字是设计不可变类的关键。它可以用来声明一个字段、方法或类：

- 当应用于类时，`final`表示这个类不能被继承。
- 当应用于方法时，`final`表示这个方法不能被子类覆盖。
- 当应用于变量时，`final`表示这个变量一旦被赋值之后就不能被改变。

对于不可变类，通常将所有的成员变量声明为`final`，这样可以保证它们只能在构造函数中被初始化一次，并且之后不能被修改。

public final class ImmutableExample {
    private final String name;

    public ImmutableExample(String name) {
        this.name = name;
    }

    public String getName() {
        return this.name;
    }
}

#### 2.2.2 类成员的不可变性

在设计不可变类时，除了将成员变量声明为`final`之外，还需要确保这些变量指向的对象也不能被修改。例如，如果类有一个成员变量引用一个可变对象的数组，那么你需要提供一个防御性的复制来避免外部修改影响到不可变对象的状态。

#### 2.2.3 构造器的使用和要求

不可变类的构造器需要保证类的不可变性。这意味着构造器必须设置所有最终字段的值，并且保证在对象构造完成之后，外部代码无法修改这些字段。

public class ImmutableClass {
    private final int value;

    public ImmutableClass(int value) {
        this.value = value;
    }

    // No setters, all state is final
}

### 2.3 实践中的不可变对象使用案例

#### 2.3.1 String类的不可变性应用

Java中的`String`类是一个典型的不可变类。一旦创建了一个`String`对象，就无法更改它所表示的字符序列。这在多线程环境中非常有用，因为不同的线程可以安全地共享字符串字面量而无需担心数据竞争问题。

String str = "Hello, immutable world!";

尽管`str`变量引用的字符串对象无法改变，但它本身可以被重新赋值，指向另一个字符串对象。

#### 2.3.2 java.time包下的不可变日期时间类

Java 8 引入了全新的日期和时间API，在`java.time`包下，大部分类都是不可变的。例如`LocalDate`、`LocalDateTime`和`ZonedDateTime`等类都是设计为不可变的，它们提供了线程安全的日期和时间操作。

LocalDate date = LocalDate.of(2023, Month.MARCH, 14);

在这个例子中，我们创建了一个`LocalDate`对象来表示2023年3月14日。这个对象一旦创建，它的状态就无法改变，这确保了在并发环境下使用这个对象时的安全性。

在下一章节中，我们将深入解析`java.time`包，探究不可变日期时间对象的创建、解析与格式化等操作，以及如何利用这些特性实现线程安全的日期时间操作。

# 3. 深入解析java.time包

## 3.1 java.time包概览
java.time包在Java 8及之后的版本中被引入，是为了替代旧的java.util.Date、java.util.Calendar以及SimpleDateFormat等类而设计的现代日期和时间API。它提供了清晰的API设计和更好的时区支持，是Java中处理日期和时间的标准库。

### 3.1.1 主要类和接口介绍
在java.time包中，主要的类和接口包括：
- **LocalDate**：表示一个没有时间的日期（年-月-日）。
- **LocalTime**：表示一个没有日期的时间（时:分:秒.纳秒）。
- **LocalDateTime**：表示一个完整的日期和时间（年-月-日 时:分:秒.纳秒），不包含时区信息。
- **ZonedDateTime**：表示一个完整的日期和时间，包含时区信息。
- **Instant**：表示时间线上的一刻，通常用于表示Unix纪元时间戳。
- **ZoneId**：表示时区ID。
- **D