MATLAB深度学习应用秘籍：构建复杂模型，解决复杂问题

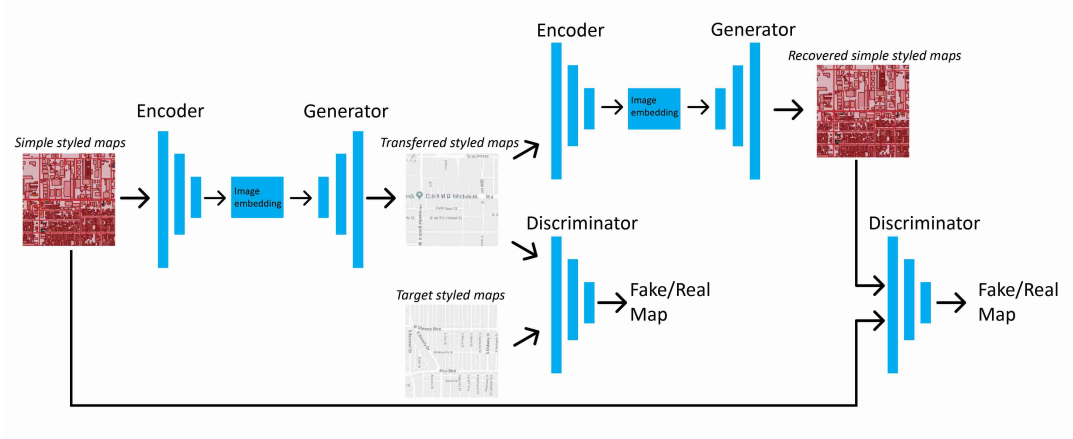
# 1. MATLAB深度学习基础

MATLAB深度学习是一种强大的技术，它使我们能够构建复杂模型来解决广泛的现实世界问题。本章将介绍MATLAB深度学习的基础知识，包括：

- **深度学习简介：**了解深度学习的概念、类型和应用。
- **MATLAB中的深度学习工具：**探索MATLAB中用于深度学习的工具和库，例如Deep Learning Toolbox和Neural Network Toolbox。
- **神经网络基础：**了解神经网络的结构、类型和训练过程。

# 2. 深度学习模型构建

### 2.1 神经网络架构设计

#### 2.1.1 卷积神经网络（CNN）

CNN 是一种专门用于处理网格状数据（如图像）的神经网络。其架构由以下层组成：

- **卷积层：**提取图像特征，使用可学习的滤波器在输入数据上滑动。
- **池化层：**减少特征图大小，提高鲁棒性。
- **全连接层：**将提取的特征映射到输出空间。

#### 2.1.2 循环神经网络（RNN）

RNN 适用于处理序列数据（如文本或时间序列）。其架构包含一个隐藏状态，该状态在处理序列的每个元素时更新。

- **基本 RNN：**最简单的 RNN 单元，具有一个隐藏状态。
- **LSTM（长短期记忆）：**一种改进的 RNN 单元，具有记忆门，可以学习长期依赖关系。
- **GRU（门控循环单元）：**另一种改进的 RNN 单元，简化了 LSTM 的结构。

#### 2.1.3 Transformer 模型

Transformer 是一种基于注意力机制的深度学习模型，用于处理序列数据。其架构包含：

- **编码器：**将输入序列转换为一组向量表示。
- **解码器：**使用注意力机制生成输出序列。
- **注意力机制：**允许模型关注序列中的特定部分。

### 2.2 训练和优化

#### 2.2.1 损失函数和优化算法

**损失函数：**衡量模型预测与真实值之间的差异。常见损失函数包括：

- **交叉熵损失：**用于分类任务。
- **均方误差：**用于回归任务。

**优化算法：**用于最小化损失函数。常见优化算法包括：

- **梯度下降：**一种迭代算法，沿梯度方向更新模型参数。
- **随机梯度下降（SGD）：**一种梯度下降的变体，每次更新使用一小批数据。
- **Adam（自适应矩估计）：**一种先进的优化算法，自适应调整学习率。

#### 2.2.2 正则化技术

正则化技术用于防止模型过拟合：

- **权重衰减：**添加一个惩罚项来限制模型权重的幅度。
- **Dropout：**在训练期间随机丢弃神经元，迫使模型学习鲁棒特征。
- **数据增强：**使用数据转换技术生成新数据，增加训练数据集的多样性。

#### 2.2.3 超参数调优

超参数是模型训练过程中的可调参数，例如学习率和正则化参数。超参数调优是通过网格搜索或贝叶斯优化等技术找到最佳超参数的过程。

# 3. 深度学习模型评估

### 3.1 评估指标

评估指标是衡量深度学习模型性能的关键因素。不同的任务类型需要不同的评估指标，以准确反映模型的有效性。

#### 3.1.1 分类任务

对于分类任务，常用的评估指标包括：

- **准确率（Accuracy）：**预测正确的样本数量与总样本数量的比率。
- **精确率（Precision）：**预测为正类的样本中，实际为正类的样本数量与预测为正类的样本数量的比率。
- **召回率（Recall）：**实际为正类的样本中，预测为正类的样本数量与实际为正类的样本数量的比率。
- **F1 分数：**精确率和召回率的加权平均值，综合考虑了模型的精确性和召回性。

#### 3.1.2 回归任务

对于回归任务，常用的评估指标包括：

- **均方误差（MSE）：**预测值与真实值之间的平方误差的平均值。
- **均方根误差（RMSE）：**均方误差的平方根。
- **平均绝对误差（MAE）：**预测值与真实值之间的绝对误差的平均值。
- **最大绝对误差（MAE）：**预测值与真实值之间的最大绝对误差。

### 3.2 模型验证和选择

模型验证和选择对于确保模型的泛化能力至关重要。

#### 3.2.1 交叉验证

交叉验证是一种用于评估模型泛化能力的技术。它将数据集随机划分为多个子集，依次使用每个子集作为测试集