CFD进阶技巧：边界条件设置与流体分析，专家级教程


参考资源链接：[使用Fluent进行UDF编程：实现自定义湍流模型](https://wenku.csdn.net/doc/5sp61tmi1a?spm=1055.2635.3001.10343)
# 1. 计算流体动力学（CFD）基础与边界条件

## 1.1 CFD的基本概念
计算流体动力学（CFD）是一种利用数值分析与数据结构技术，对流体流动和热交换问题进行分析和解决的科学。CFD技术通过计算机模拟，可以在无需实际构建物理模型的情况下，预测和可视化复杂流体动力学问题的行为。

## 1.2 CFD的工作流程
CFD分析通常遵循以下步骤：定义问题和目标、创建几何模型、网格划分、设置边界条件、选择合适的数值方法、求解计算以及分析结果。边界条件在CFD中起着至关重要的作用，它们为模型提供了必要的外部约束。

## 1.3 边界条件的作用
在CFD分析中，边界条件定义了计算域边界上的物理条件，如速度、压力和温度等。它们直接影响流体的流动和热传递特性。根据不同的实际应用场景，边界条件可以分为多种类型，比如速度入口、压力出口、壁面条件等。选择正确的边界条件是获得准确CFD分析结果的关键。

# 2. 边界条件的分类与设置

### 2.1 边界条件的理论基础
边界条件是计算流体动力学（CFD）模型中的关键部分，它们为流体域提供了必要的数学描述，使得方程具有唯一解。边界条件通常基于物理现象和实验数据来定义，以确保模拟结果的准确性和可靠性。

#### 2.1.1 物理模型与数学方程
在CFD中，流体行为由Navier-Stokes方程来描述，这是一组偏微分方程，包括连续性方程、动量方程和能量方程。为了封闭这些方程，需要引入物理模型，如湍流模型、燃烧模型等。物理模型通过数学形式对实际流体特性进行近似，以简化复杂的流动现象。

#### 2.1.2 边界条件类型概述
边界条件分为多种类型，包括 Dirichlet 边界条件（指定变量值）、Neumann 边界条件（指定变量的导数值）以及Robin 边界条件（结合了以上两种）。每种类型的边界条件对应不同的物理意义，如在壁面附近可能使用无滑移条件（Dirichlet），在远场边界可能使用自由流条件（Neumann）。

### 2.2 定压和定温边界条件的设置
定压和定温边界条件是CFD中常见的边界条件，它们分别用于模拟流体在恒定压力和恒定温度下的行为。

#### 2.2.1 定压边界条件的应用场景
定压边界条件在涉及压力变化显著的流动问题中尤为重要，例如在流体进入或离开开放空间时。在实际应用中，如喷嘴设计、阀门分析等，使用定压边界条件可以模拟流体与外界环境的交互。

flowchart LR
    A[开始模拟] --> B[应用定压边界条件]
    B --> C[计算流场]
    C --> D[确定流体在开放空间的行为]
    D --> E[结束模拟]

#### 2.2.2 定温边界条件的实现方法
定温边界条件用于模拟流体与固体壁面或其他介质间的热交换过程。在模型中引入定温边界条件，有助于理解热效应对流体流动的影响，例如在发动机冷却系统的设计中，定温边界条件可用来模拟冷却水流动。

flowchart LR
    A[开始模拟] --> B[应用定温边界条件]
    B --> C[计算热交换]
    C --> D[分析热效应影响]
    D --> E[结束模拟]

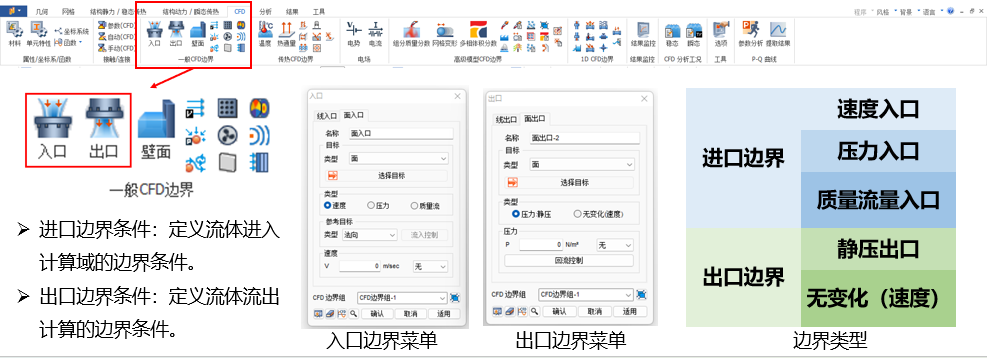
### 2.3 入口和出口边界条件的设置
入口和出口边界条件对于CFD模型中的流场分析至关重要，因为它们定义了流体流动的起始和终止条件。

#### 2.3.1 入口边界条件的参数选择
入口边界条件涉及多个参数，如速度剖面、温度、湍流强度和湍流尺度等。选择正确的参数对于模拟的准确性至关重要。在实际应用中，例如模拟风洞实验时，需要根据实验条件选择合适的入口边界条件参数。

flowchart LR
    A[选择入口边界条件] --> B[定义速度剖面]
    B --> C[设置温度参数]
    C --> D[调整湍流参数]
    D --> E[输入边界条件到模拟软件]

#### 2.3.2 出口边界条件的流态影响
出口边界条件的设置对流态具有显著影响，需要根据流体流动的预期来选择。在开放性出口的情况下，通常采用压力出口边界条件，允许流体自由地流出模拟区域。对于闭合出口，可能需要设置特定的压力或回流条件以维持流动的连续性。

flowchart LR
    A[定义出口边界条件] --> B[判断流态]
    B --> C{是否开放出口?}
    C --> |是| D[应用压力出口条件]
    C --> |否| E[应用闭合出口条件]
    D --> F[模拟流体自由流出]
    E --> G[保持流动连续性]

通过本章节的介绍，我们了解到边界条件在CFD模型中的重要性，它们是模拟流体动力学行为的基础。下一章节将详细讨论流体分析的数值方法，进一步深化对CFD仿真的理解。

# 3. 流体分析的数值方法

## 3.1 离散化技术

### 3.1.1 网格划分的原理和方法

在计算流体动力学（CFD）的数值模拟中，网格划分是将连续的物理空间离散化为有限数量的控制体积（或称单元），以便进行数值求解。网格的类型和密度会直接影响到数值模拟的准确性和计算效率。以下为几种常见的网格划分技术：

**结构网格：** 也被称为规则网格，是一种具有规律排列的网格系统，适用于几何形状简单，边界光滑的模型。结构网格的优点是生成速度快，计算精度高，但是难以适应复杂的几何结构。

graph TD;
A[开始] --> B[选择结构网格方法];
B --> C[定义边界和网格分布];
C --> D[生成网格];
D --> E[进行CFD分析];

**非结构网格：** 非结构网格由不规则的四面体、六面体或其他多面体单元组成，能够较好地适应复杂的几何形状。虽然非结构网格在生成和求解时更加灵活，但它通常需要更多的计算资源。

**混合网格：** 混合网格结合了结构网格和非结构网格的优点，适用于复杂的流体动力学分析。混合网格通过在流体区域的关键部分使用非结构网格，而在影响较小的区域使用结构网格来减少计算资源的消耗。

**贴体网格：** 贴体网格特别适用于模拟具有复杂边界条件的流场，如圆管、绕流等。通过贴合物体表面，这类网格能更准确地描述边界层内的流体行为。

### 3.1.2 离散化误差的来源与控制

离散化误差是由于用有限数量的网格来近似连续物理场而产生的误差。减少离散化误差的常用方法包括：

**网格加密：** 在流场中重要的区域（如边界层、激波、复杂几何的角落等）加密网格可以提高计算精度。

**更高阶的离散格式：** 如二阶迎风、 QUICK (Quadratic Upstream Interpolation for Convective Kinematics) 格式等，可以提供比一阶迎风格式更高的计算精度。

**多重网格技术：** 使用多层不同密度的网格来求解流体方程，通过在不同网格层之间传递信息来加速收敛和提高精度。

### 代码块和逻辑分析

# Python示例代码，生成非结构化四面体网格
import gmsh

# 定义几何模型尺寸
length = 1.0
width = 0.5
height = 0.1

# 定义几何体
points = [gmsh.model.geo.addPoint(x, y, z) for x, y, z in [
    (0, 0, 0), (length, 0, 0), (length, width, 0), (0, width, 0),
    (0, 0, height), (length, 0, height), (length, width, height), (0, width, height)

# 定义线和面
lines = [gmsh.model.geo.addLine(p1, p2) for p1, p2 in [
    (points[0], points[1]), (points[1], points[2]), (points[2], points[3]), (points[3], points[0]),
    (points[4], points[5]), (points[5], points[6]), (points[6], points[7]), (points[7], points[4]),
    (points[0], points[4]), (points[1], points[5]), (points[2], points[6]), (points[3], points[7])

# 形成外边界
loop = gmsh.model.geo.addCurveLoop(lines[:4])
surface = gmsh.model.geo.addPlaneSurface([loop])

# 生成体积
volume = gmsh.model.geo.addVolume([surface])

# 网格化几何体
gmsh.model.geo.synchronize()
gmsh.model.mesh.generate(3)

# 输出网格信息
nodes, elements, _, _, _ = gmsh.model.mesh.getNodesAndElements()
print("节点数量：", len(nodes))
print("单元数量：", len(elements))

在上述代码中，我们使用gmsh库生成了一个立方体的几何模型并对其进行了网格划分。`gmsh.model.geo.addCurveLoop` 和 `gmsh.model.geo.addPlaneSurface` 的函数调用创建了一个面，并最终通过`gmsh.model.mesh.generate(3)`生成了一个三维网格。代码还展示了如何获取生成的节点和单元数量。这样的网格划分技术能够让我们根据CFD分析的需求灵活定义计算网格。

## 3.2 求解器的选用与配置

### 3.2.1 流体动