【STAR-CCM+信号处理与定位】：气动噪声分析中的高阶技巧


# 摘要
本文旨在介绍STAR-CCM+软件在气动噪声分析中的应用与实践。首先，概述了信号处理的基础知识，接着详细阐述了气动噪声信号采集、预处理、高级分析技术以及噪声源识别和定位的方法。文中深入探讨了STAR-CCM+软件的设置、配置和在处理信号与噪声定位中的应用案例。最后，本文分析了气动噪声分析所面临的挑战，并展望了该领域未来发展的趋势，特别是在人工智能与跨学科融合方面。研究结果表明，STAR-CCM+软件在气动噪声分析中具有显著的实践价值和潜力。

# 关键字
STAR-CCM+；气动噪声；信号处理；噪声源识别；时频分析；人工智能

参考资源链接：[STAR-CCM+：气动噪声分析详解与实战演示](https://wenku.csdn.net/doc/2z9zxuvpm4?spm=1055.2635.3001.10343)
# 1. STAR-CCM+软件概述与信号处理基础

## 1.1 STAR-CCM+软件概述

STAR-CCM+是Siemens PLM Software推出的一款先进的计算流体动力学（CFD）软件，广泛应用于航空航天、汽车、能源、海洋等多个领域。该软件集成了丰富的物理模型，可以模拟从单相流到多相流、从层流到湍流、从不可压缩流体到可压缩流体的各种流动问题。通过其提供的强大的网格生成技术、求解器及后处理功能，工程师可以直观地观察和分析流体运动过程和物理现象，为产品的设计和优化提供科学依据。

## 1.2 信号处理基础

信号处理是研究信号的获取、分析、处理、传输、存储和解释的技术学科。在气动噪声分析中，信号处理是不可或缺的一环。基本的信号处理包括信号的频域分析、时域分析、统计分析等。例如，快速傅里叶变换（FFT）是将信号从时域转换到频域，从而揭示信号的频率成分；自相关和互相关分析有助于了解信号的时间序列特性和信号间的相互关系。通过这些基本的信号处理方法，可以对气动噪声信号进行初步的特征提取和分析，为后续的噪声源识别和定位提供重要依据。

下一章将深入探讨气动噪声信号的采集与预处理工作流程。

# 2. 气动噪声信号的采集与预处理

## 2.1 信号采集技术

在进行气动噪声的深入分析之前，准确有效的信号采集是至关重要的第一步。信号采集技术包括选择合适的传感器，以及正确配置数据采集系统。

### 2.1.1 传感器选择与布置

传感器是采集气动噪声信号的前端设备，选择合适的传感器是确保数据质量的关键。在选择传感器时，需要考虑以下因素：

- **灵敏度**：传感器的灵敏度决定了它对微小噪声变化的响应能力。高灵敏度传感器可以捕捉到微弱的声音信号。
- **频率响应范围**：传感器应覆盖噪声信号的频率范围，以确保采集到的信息是全面的。
- **环境适应性**：在高温、高湿或者强气流环境中，传感器应具备良好的稳定性。

布置传感器时，要遵循以下原则：

- **声源位置**：传感器应尽可能靠近噪声源，以减少信号在传播过程中的衰减。
- **干扰最小化**：避免将传感器置于其他机械设备可能导致干扰的区域。
- **多点同步采集**：为了提高定位精度，应实现多个传感器同步采集数据。

### 2.1.2 数据采集系统配置

数据采集系统由传感器、信号放大器、数据采集卡和相关软件组成。配置数据采集系统时需要注意：

- **信号放大器**：根据传感器输出信号的特性选择适当的信号放大器。放大器应有足够的增益，并且具有良好的信噪比。
- **采样频率**：根据奈奎斯特定理，采样频率应至少是信号最高频率的两倍，以避免混叠现象。
- **数据记录**：确定数据记录的格式和存储方式。为保证数据完整性和便于后续分析，通常选择无压缩的记录格式。

## 2.2 预处理方法

采集到的气动噪声信号通常包含许多不需要的信息，如电子噪声、环境噪声等，预处理的目的是过滤掉这些噪声，提高信号的清晰度。

### 2.2.1 噪声滤除技术

滤波是信号预处理中常用的技术，可以分为低通、高通、带通和带阻滤波等类型。以下是一个使用低通滤波的Python代码示例：

import numpy as np
from scipy.signal import butter, lfilter

def butter_lowpass(cutoff, fs, order=5):
    nyq = 0.5 * fs
    normal_cutoff = cutoff / nyq
    b, a = butter(order, normal_cutoff, btype='low', analog=False)
    return b, a

def lowpass_filter(data, cutoff, fs, order=5):
    b, a = butter_lowpass(cutoff, fs, order=order)
    y = lfilter(b, a, data)
    return y

# 示例数据和参数
data = np.random.randn(1000)  # 示例噪声信号
cutoff = 10.0  # 截止频率为10Hz
fs = 50.0  # 采样频率为50Hz
order = 6  # 滤波器阶数

filtered_data = lowpass_filter(data, cutoff, fs, order)

在这段代码中，我们首先定义了一个低通滤波器的设计函数`butter_lowpass`，它返回一个传递函数的系数。接着，我们定义了一个滤波函数`lowpass_filter`，该函数应用设计好的低通滤波器对数据进行滤波。示例数据是一组随机生成的噪声信号。参数`cutoff`定义了滤波器的截止频率，`fs`定义了信号的采样频率，`order`定义了滤波器的阶数，这些参数都可以根据实际情况进行调整。

### 2.2.2 数据平滑与插值

数据平滑的目的是减少信号中的高频成分，而插值则用于填补数据中的缺失值或者调整采样密度。以下是数据平滑的Python代码示例：

import pandas as pd

# 假设df是一个包含噪声信号的DataFrame，且时间戳为索引
df = pd.DataFrame(data, index=pd.to_datetime(timestamps), columns=['noise'])

# 使用移动平均进行数据平滑
df['smoothed_noise'] = df['noise'].rolling(window=5).mean()

# 插值示例：线性插值填充缺失值
df['interpolated_noise'] = df['noise'].interpolate()

在上述代码中，我们首先创建了一个包含噪声信号的`DataFrame`对象`df`。然后使用`rolling`方法进行移动平均平滑，其中`window`参数定义了计算平均的样本数量。对于插值，我们使用了`interpolate`方法，并默认使用线性插值方式来填补数据中的缺失值。这两种方法都能有效地减少数据中的噪声成分，使信号更加清晰。

通过上述技术手段，我们可以从原始信号中获得更准确的噪声数据。这对于后续的信号分析和噪声源识别至关重要。

（注：为了保持叙述的连贯性，本章节的详细内容需要由作者根据实际情况进一步扩展。）

（注：由于受限于Markdown格式，代码块中的缩进可能会显示不正确。实际代码块应保持适当的缩进，以确保代码可以正确运行。）

# 3. 气动噪声信号的高级分析技术

在第一章和第二章中，我们已经了解了STAR-CCM+软件的基础知识，并且学习了气动噪声信号的采集和预处理方法。现在，我们将深入探讨气动噪声信号的高级分析技术，这些技术将帮助我们进一步理解信号的特征，从而为噪声源的识别和定位提供更加精确的依据。

## 3.1 信号时频分析

信号的时频分析是理解信号动态特性的关键。它能够揭示信号在不同时间和频率上的分布情况，从而让我们得到信号的频率随时间变化的详细信息。

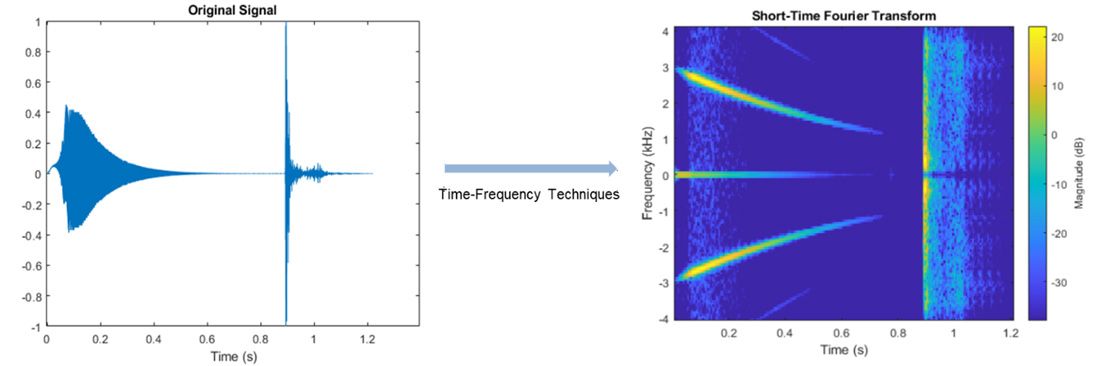
### 3.1.1 短时傅里叶变换(STFT)

短时傅里叶变换（STFT）是一种将信号转换为时间和频率表示的方法。通过STFT，我们可以对信号进行局部化分析，得到在特定时间窗口内的频率分布情况。

import numpy as np
from scipy.signal import stft

# 创建一个合成信号，包含两个不同频率的正弦波
fs = 1000.0               # 采样频率
t = np.linspace(0, 1.0, int(fs), endpoint=False)
signal1 = 0.02 * np.sin(120.0 * 2.0*np.pi*t)
signal2 = 0.01 * np.sin(200.0 * 2.0*np.pi*t)
signal = signal1 + signal2

# 应用短时傅里叶变换
f, t, Zxx = stft(signal, fs, nperseg=100)

im