梯度提升树的并行化策略：训练效率提升的秘诀

# 1. 梯度提升树模型概述

在机器学习领域，梯度提升树（Gradient Boosting Tree，GBT）是一种广泛使用的集成学习算法，以其高效性、灵活性和模型解释性而受到青睐。本章将首先介绍梯度提升树的历史背景和发展，然后阐述其与随机森林等其他集成算法的区别和联系，为读者提供一个关于梯度提升树模型的全面概述。

梯度提升树模型最初由J. H. Friedman在1999年提出，灵感来源于前向分步算法和提升方法，其核心思想是通过迭代的方式逐步构建多个弱学习器，并将其串联起来以形成一个强学习器。梯度提升树在分类、回归以及排序等任务中都有出色的表现，尤其在处理结构化数据方面，它能够构建复杂且准确的决策边界。

不同于随机森林等基于随机选择的集成模型，梯度提升树强调在前一个模型的错误上进行逐步改进，通过优化损失函数来逼近真实输出。这种方法使得梯度提升树通常比随机森林具有更高的准确度，但同时也可能带来过拟合的风险。本章的后续内容将对梯度提升树的算法原理、数学基础和实现步骤进行深入探讨。

# 2. 梯度提升树的核心算法原理

在第一章中，我们对梯度提升树模型有了一个大致的了解。本章将深入探讨梯度提升树的核心算法原理，包括其基本概念、数学基础以及算法步骤的详解，为我们深入理解和应用梯度提升树奠定理论基础。

## 2.1 梯度提升树的基本概念

### 2.1.1 梯度提升框架的起源和发展

梯度提升技术起源于20世纪90年代，最初用于解决回归问题，随后逐步扩展到分类问题以及更复杂的机器学习任务中。它的核心思想是通过组合多个弱学习器（通常是决策树）来构建一个强学习器。弱学习器的特点是仅比随机猜测略好，但它们可以捕捉数据中的某些模式。

梯度提升框架的发展经历了几个重要的里程碑。首先是梯度提升回归树（Gradient Boosting Regression Tree, GBR）的提出，紧接着是梯度提升决策树（Gradient Boosting Decision Tree, GBDT）的广泛应用。这些模型在各种机器学习竞赛中屡获佳绩，如Kaggle比赛，证明了其强大的预测能力和泛化性能。

### 2.1.2 梯度提升树与随机森林的比较

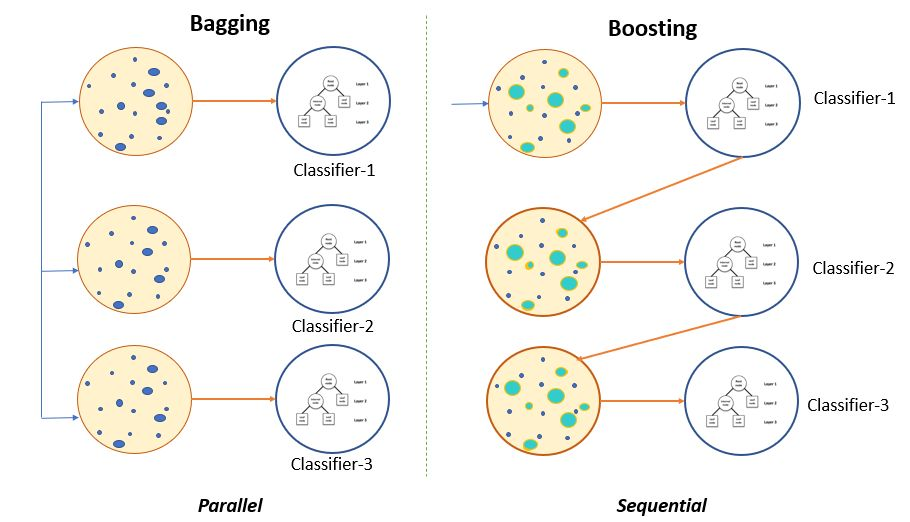
梯度提升树与随机森林都是集成学习方法，它们都通过组合多个基学习器来提高模型性能，但它们的工作机制和优化目标存在显著差异。

随机森林通过构建多个深度不同的决策树，每一棵树在训练时都会在输入特征和样本上引入随机性，通过投票或平均的方式输出最终结果。其优点在于对异常值和噪声具有很强的鲁棒性，同时能够处理大规模数据集。

梯度提升树则通过迭代地添加新的树模型，每一次添加都基于前一轮模型的残差进行优化，最终得到一个强学习器。其优点在于能够对模型的预测进行连续的优化，往往可以获得比随机森林更高的精度。

## 2.2 梯度提升树的数学基础

### 2.2.1 损失函数的梯度计算

在梯度提升框架中，损失函数用于衡量模型预测值与真实值之间的差异。在不同的问题中，可能需要选择不同的损失函数，如均方误差（MSE）、对数损失（Log Loss）等。

梯度提升算法的基本思想是：在每一步迭代中，都通过最小化损失函数的梯度来添加新的基学习器。具体的，对于回归问题，损失函数通常是关于预测值的函数，梯度则是损失函数关于预测值的导数。在每次迭代过程中，通过计算损失函数相对于当前模型预测的梯度，来确定新的基学习器应该如何调整以减少损失。

### 2.2.2 基学习器的选择和优化

在梯度提升树中，基学习器主要是决策树，尤其是回归树。基学习器的选择和优化是提升性能的关键因素。一棵好的基学习器应该能够捕捉到数据中残差的模式，并且足够简单以避免过拟合。

决策树的深度、节点的分裂方式、分裂点的选择等都会影响到模型的性能。在梯度提升过程中，通常会限制决策树的深度，以防止模型变得过于复杂。同时，会采用如正则化参数来控制模型的复杂度和过拟合的风险。

## 2.3 梯度提升树的算法步骤详解

### 2.3.1 迭代提升过程

梯度提升树的算法过程是迭代的。初始时，我们用一个简单的模型（通常是常数模型）开始，然后进行多次迭代，每一次迭代都会添加一个新的基学习器。在每一次迭代中，会根据上一次迭代的预测残差来训练新的基学习器。

具体来说，第t轮迭代的目标是找到一棵树，它能够最好地拟合之前所有树预测结果与实际标签之间的负梯度（即残差）。这个过程是通过最小化损失函数来完成的，通常采用贪心算法来搜索最佳分裂点和分裂方式。

### 2.3.2 正则化策略和剪枝技术

正则化策略是控制模型复杂度、预防过拟合的重要手段。在梯度提升树中，常用的正则化方法包括树的深度限制、叶子节点的最小样本数以及学习率。

剪枝技术则是在训练完一棵树后对树进行简化，去除一些对最终预测结果影响不大的节点。这可以减少模型的复杂度，并可能提高模型的泛化能力。

例如，预剪枝是提前停止树的生长，当一个节点的分裂不再显著降低目标函数时停止分裂。后剪枝则是在树完全生长后，通过评估不同子树的性能，合并那些对最终预测结果影响不大的子树。

通过本章的讨论，我们已经了解了梯度提升树模型的核心原理。下一章我们将探讨梯度提升树并行化的理论基础及其应用实践，进一步深入模型的应用层面。

# 3. 并行化策略的理论与实践

随着数据规模的不断膨胀和计算需求的日渐增长，传统的串行计算模型已经难以满足大规模机器学习任务的计算需求。梯度提升树（Gradient Boosting Tree，GBT）作为一种强大的集成学习算法，在处理大规模数据集时，