FLACS自适应网格技术：智能调整网格的高级策略


# 摘要
本文全面探讨了FLACS自适应网格技术的理论基础、实现优化、应用案例及面临的挑战和发展趋势。首先介绍了FLACS自适应网格技术的概念，然后详细阐述了其理论基础、FLACS软件中的应用特点以及相关的数学基础。接着，本文重点讨论了自适应网格技术的实现策略，包括网格生成与调整算法、计算效率优化以及在特定案例中的应用。此外，文章还分析了当前技术的局限性和面临的计算挑战，并展望了自适应网格技术的未来发展方向，尤其是跨学科应用的潜力。最后，通过对实际案例的研究、软件实现和性能测试，本文对FLACS自适应网格技术的实际应用和性能进行了评估，并对未来发展进行了展望。

# 关键字
FLACS；自适应网格技术；网格生成；计算效率；案例研究；性能测试

参考资源链接：[FLACS 8用户手册：3D模拟爆炸与环境影响分析的关键工具](https://wenku.csdn.net/doc/6fkzhigpko?spm=1055.2635.3001.10343)
# 1. FLACS自适应网格技术概述

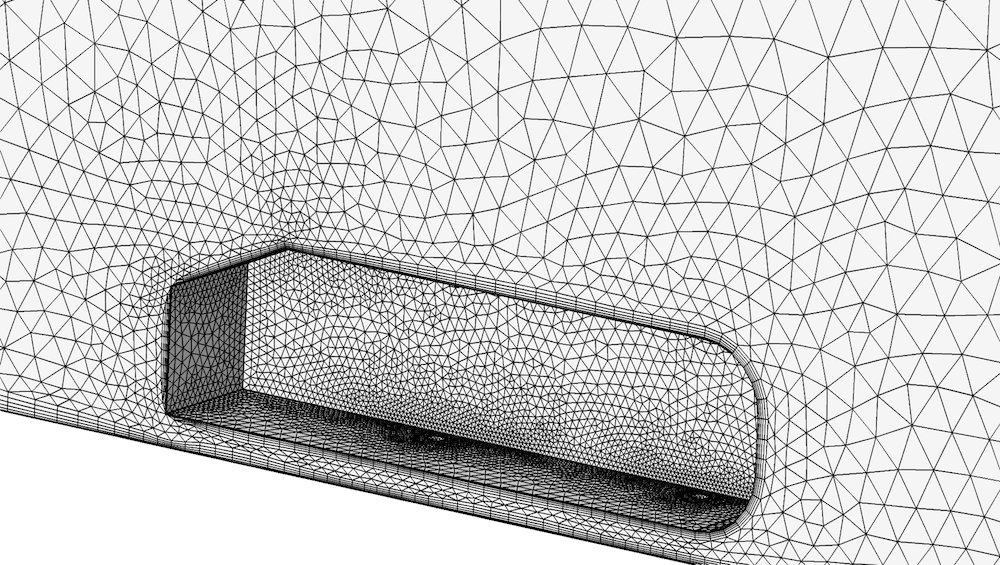
在计算机模拟和计算流体动力学(CFD)领域，FLACS软件因其对复杂场景中气体爆炸和火灾模拟的高效性而被广泛应用于工业安全分析。自适应网格技术作为FLACS的核心，它不仅提高了模拟精度，还优化了计算资源的使用。本章将概述FLACS中的自适应网格技术，为理解后续章节中更为详细的技术分析和应用实例打下基础。自适应网格技术允许在计算过程中根据解的特征动态调整网格的密度，从而在关键区域提供更高的精度，同时在变化不大的区域减少计算负担。这种技术显著提高了模拟的效率和精确度，尤其是在处理爆炸和火灾这类动态变化剧烈的问题时，能够更精确地捕捉到流体动力学的变化。

# 2. 理论基础与自适应网格技术

## 2.1 自适应网格技术的理论框架

### 2.1.1 网格自适应的基本原理

自适应网格技术，简而言之，是让计算网格能够根据问题的特性自动调整自身结构以提高计算精度和效率的算法。其核心思想在于依据局部误差估计，动态优化网格分布，实现局部细化或粗糙化处理。

网格自适应算法通常包括误差估计、网格生成、映射变换和网格光滑等关键步骤。误差估计是为了识别出模拟过程中的关键区域并生成更密集的网格以提升模拟精度。网格生成是创建符合误差估计结果的网格结构。映射变换确保物理变量在新旧网格之间的连续性，而网格光滑则是为了提高网格质量，避免过度扭曲。

在网格自适应过程中，重要的是保持网格质量和适应性的同时，尽可能地控制计算成本。具体操作中，会使用不同的策略来达成上述目标，比如局部细化、网格合并、节点移动等方法。

### 2.1.2 网格自适应的关键技术

网格自适应的关键技术包含局部误差估计方法、动态网格管理技术、以及各种网格优化算法。

局部误差估计技术主要有基于物理量梯度的方法、残差估计方法以及特征线法等。这些技术通过分析计算结果的局部差异来确定网格应如何调整。

动态网格管理技术主要处理网格的生成、调整和删除过程，确保网格的动态适应性。它涉及到复杂的数据结构和算法，比如二叉树、四叉树或者八叉树等，用于管理网格单元的父子关系。

网格优化算法，如网格光滑和网格平衡技术，则用于优化网格质量，提高数值计算的稳定性和准确性。例如，Laplace网格光滑算法通过迭代调整网格节点位置来减少网格扭曲。

## 2.2 FLACS软件中的自适应网格方法

### 2.2.1 FLACS软件介绍

FLACS，全称为Fire, Explosion, and Gas Dispersions Simulator，是一款专门用于模拟气体爆炸、火灾蔓延和气体扩散的专业仿真软件。它被广泛应用于工业安全评估、环境影响分析和安全工程设计等领域。

FLACS软件采用先进的计算流体动力学（CFD）技术，结合自适应网格技术，可以在复杂的几何环境中实现高精度的模拟计算。自适应网格技术允许FLACS在模拟过程中根据流场特性自动调整网格的密度和大小，从而在保证计算精度的同时提高计算效率。

### 2.2.2 FLACS中的网格技术特点

FLACS中的自适应网格技术体现在其动态网格调整功能。在模拟开始之前，FLACS会根据设定的初始条件和计算域的几何特性生成初始网格。随后，在模拟过程中，FLACS根据预设的误差估计策略和目标误差水平动态地调整网格。

这些网格调整策略包括：在流体流动剧烈、温度梯度大、压力变化显著的区域进行网格细化，而在变化平缓的区域则减少网格密度。此外，FLACS也支持局部网格细化以提高特定区域的模拟精度，这在处理如障碍物周围的流动和复杂边界条件时尤为重要。

FLACS的自适应网格技术还能够保证网格的连续性，避免因网格调整导致的数值解不连续性问题。软件通过插值算法确保物理变量在网格转换过程中的连续性。

## 2.3 高级自适应网格策略的数学基础

### 2.3.1 有限元分析与网格细化

有限元分析（FEA）是分析复杂工程问题的一种数值计算方法。它将一个大的连续域划分为更小的、更易处理的子域（即元素），通过求解每个元素的局部方程来近似求得整个域的解。

在FLACS中，有限元分析与网格细化相结合，使得软件能够在计算过程中自适应地调整网格。这种自适应细化技术包括p-细化（多项式阶数细化）和h-细化（网格大小细化）。p-细化通过提高元素的多项式阶数来提升计算精度，而h-细化通过减小元素的尺寸来达到相同的目的。

### 2.3.2 多重网格技术与迭代求解

多重网格技术是解决大规模稀疏线性系统的有效方法。它通过在不同的网格层次上进行迭代求解，加速迭代过程，从而提升计算效率。多重网格技术的核心思想是利用粗网格层的快速迭代，来估计细网格层迭代误差的变化趋势。

在FLACS中，多重网格技术配合迭代求解器，可以提高大型CFD问题求解的速度与稳定性。通过在不同精度层次的网格上交替迭代，多重网格技术可以快速减少整体的数值误差。

在多重网格技术中，每层网格上的迭代过程通常是迭代求解器的一种，比如共轭梯度法（CG），双共轭梯度法（Bi-CG）等。这些求解器通过迭代过程逐步逼近线性系统的解。同时，多重网格方法中会引入平滑过程，如高斯-赛德尔（Gauss-Seidel）迭代等，帮助消除高频误差分量，进一步提高数值解的精确度。

通过多重网格技术的应用，FLACS在进行复杂的爆炸和火灾模拟时，能够更加高效地处理大规模的计算问题，提供准确且可靠的模拟结果。

# 3. 自适应网格技术的实现与优化

## 3.1 网格生成与调整算法

### 3.1.1 网格生成算法简介

在进行复杂的物理模拟或计算流体动力学（CFD）分析时，网格生成算法是构建数值模型的基础。传统的网格生成方法包括结构化网格和非结构化网格。结构化网格通常用于简单几何区域，其优势在于规则的拓扑结构，便于实施边界条件和算法优化。而非结构化网格适用于复杂几何区域，提供了更高的灵活性。随着计算需求的提升，自适应网格生成技术逐渐成为了优化数值模拟的核心方法。

自适应网格技术的核心在于根据求解过程中的物理量变化，动态调整网格的密度。这就意味着在物理量变化剧烈的区域，网格会自动细化以提高计算精度；而在变化较小的区域，则可能采用较粗的网格以节省计算资源。自适应网格生成算法通常分为几类：基于误差估计的自适应，基于特征提取的自适应，以及基于解后处理的自适应。每种方法在网格密度调整的依据上有所区别，但都需要精确的数学模型和高效的算法来支撑。

以基于误差估计的自适应网格技术为例，该方法通常包括误差指示器的构建、误差估计和网格更新三个主要步骤。误差指示器可以是基于残差的，也可以是基于解的导数。误差估计则需要评估当前网格下的解的精度，通常是通过比较不同网格级别下解的差异来实现。网格更新则是根据误差估计的结果，增加或减少网格的细化程度。

### 3.1.2 网格调整的实时性和精确性