深度学习中的超参数敏感性分析：关键参数的识别技巧

# 1. 超参数敏感性分析简介

在深度学习模型的训练过程中，超参数的选择往往直接影响模型的性能。这些参数如学习率、批量大小等，在模型的训练过程中起到关键作用。超参数敏感性分析是研究不同超参数对模型性能影响的过程，它有助于我们更深层次地理解模型的内在工作机制，并指导我们在实际应用中做出更为合理的超参数选择。

本章将简要介绍超参数敏感性分析的必要性和基本概念，为后续章节的理论基础、分析方法以及实践案例打下坚实的基础。

- **超参数的定义**：超参数是外部设定的参数，不是通过训练数据学习得到的。它控制着学习过程和模型结构的高级属性。
- **敏感性分析的重要性**：通过分析超参数对模型性能的影响，可以找到最优化超参数组合，减少过拟合和欠拟合的风险。
- **分析的目的**：为数据科学家和机器学习工程师提供决策支持，通过系统化地评估超参数的影响来提升模型训练的效率和准确性。

让我们继续深入探索超参数的理论基础及其分类，为开展有效的超参数敏感性分析做好准备。

# 2. 理论基础与超参数分类

## 2.1 超参数定义及其在深度学习中的作用

### 超参数与模型参数的区别

在深度学习模型中，超参数和模型参数是两个截然不同的概念。模型参数，如神经网络中的权重和偏置，是通过学习过程从数据中得到的，它们定义了模型的具体行为。而超参数则是指在学习过程之前设定的，对学习过程有重大影响的参数，它们定义了模型的学习过程。超参数的设置不是通过训练得到的，而是通过经验、实验或交叉验证来决定。

### 超参数的类型和范围

超参数的类型和范围非常广泛，包括但不限于学习率、网络层数、每层的神经元数、激活函数的选择、批量大小、正则化系数等。它们可以分为两类：结构超参数和训练超参数。结构超参数涉及网络的架构，如层数和神经元数；训练超参数包括学习率和批量大小等，影响模型的训练过程。

graph TD
    A[超参数] --> B[结构超参数]
    A --> C[训练超参数]
    B --> D[层数]
    B --> E[每层神经元数]
    C --> F[学习率]
    C --> G[批量大小]

## 2.2 常见超参数的作用与影响

### 学习率的选择与调整

学习率是控制模型在参数空间中搜索最优解的速度。如果学习率太高，模型可能会在最优解附近振荡甚至发散；而如果学习率太低，模型的学习过程会变得缓慢，甚至有可能陷入局部最优解。因此，合适的学习率选择和调整对于模型训练至关重要。

### 批量大小与网络训练稳定性

批量大小是指在一次训练迭代中所使用的训练样本数量。它对网络训练的稳定性有显著影响。较小的批量大小可以提供更加稳定的梯度估计，但同时会带来较大的方差。较大的批量大小则反之。理想的批量大小应当能够平衡训练的稳定性和效率。

### 正则化参数与模型泛化能力

正则化参数，如L1和L2惩罚项的系数，用于控制模型复杂度，防止过拟合。正则化可以增强模型的泛化能力，但过度的正则化会导致欠拟合。因此，选择合适的正则化参数，也是实现模型优化的关键步骤之一。

| 超参数类型 | 示例 | 影响 | 注意事项 |
| ---------- | ---- | ---- | -------- |
| 学习率 | 0.01, 0.001 | 控制优化速度和稳定 | 需要根据任务和模型调整 |
| 批量大小 | 32, 64, 128 | 影响梯度估计和训练稳定性 | 需平衡速度和内存消耗 |
| 正则化参数 | L2: 0.01, L1: 0.001 | 控制模型复杂度防止过拟合 | 通常需要交叉验证确定最佳值 |

import tensorflow as tf

# 示例：使用TensorFlow定义学习率调整策略
lr_schedule = tf.keras.optimizers.schedules.ExponentialDecay(
    initial_learning_rate=0.01,
    decay_steps=10000,
    decay_rate=0.9,
    staircase=True)

optimizer = tf.keras.optimizers.Adam(learning_rate=lr_schedule)

以上代码块展示了如何在TensorFlow中使用学习率衰减策略。在初始学习率设置为0.01后，每10000个训练步骤，学习率将按照0.9的比例进行衰减。这是一种常用的策略，有助于在训练初期快速收敛，并在训练后期通过减小学习率避免过度振荡。

# 3. 超参数敏感性分析方法

在深度学习模型的训练过程中，超参数的选择对最终模型性能的影响至关重要。为了找到最优的超参数配置，研究者和工程师们需要借助一系列的方法进行敏感性分析。本章节将深入探讨这些分析方法，提供理论基础，并详细描述不同分析技术的具体应用。

## 3.1 敏感性分析的理论与技术框架

### 3.1.1 敏感性分析的概念模型

在研究超参数对模型性能影响的过程中，敏感性分析是通过评估模型输出（性能指标）对输入超参数变化的反应来确定哪些超参数对模型性能最为关键。这种分析通常涉及到系统地改变超参数值，并观察模型表现的变化。

敏感性分析的概念模型通常包含以下几个要素：

- **输入变量**：超参数本身，例如学习率、批量大小、正则化系数等。
- **输出响应**：通过超参数的不同配置，我们观测到的模型性能指标，如准确率、损失值、ROC曲线下面积（AUC）等。
- **不确定性分析**：由于随机初始化和数据划分的随机性，通常模型性能具有一定的不确定性，敏感性分析需要考虑到这一点。

### 3.1.2 分析方法的分类与选择

敏感性分析的方法多种多样，大致可以分为定性和定量两大类。定性方法主要是基于观察和经验的判断，而定量方法则通过数学和统计学方法来评估超参数的影响力。

在选择适当的分析方法时，需要考虑模型的复杂度、计算资源、可解释性需求等因素。对于简单的模型，可以使用定性方法进行初步分析。但对于深度学习模型，尤其是参数众多的模型，定量方法更加适用，因为它们能够提供更为精确和系统的分析结果。

## 3.2 实验设计与统计学方法

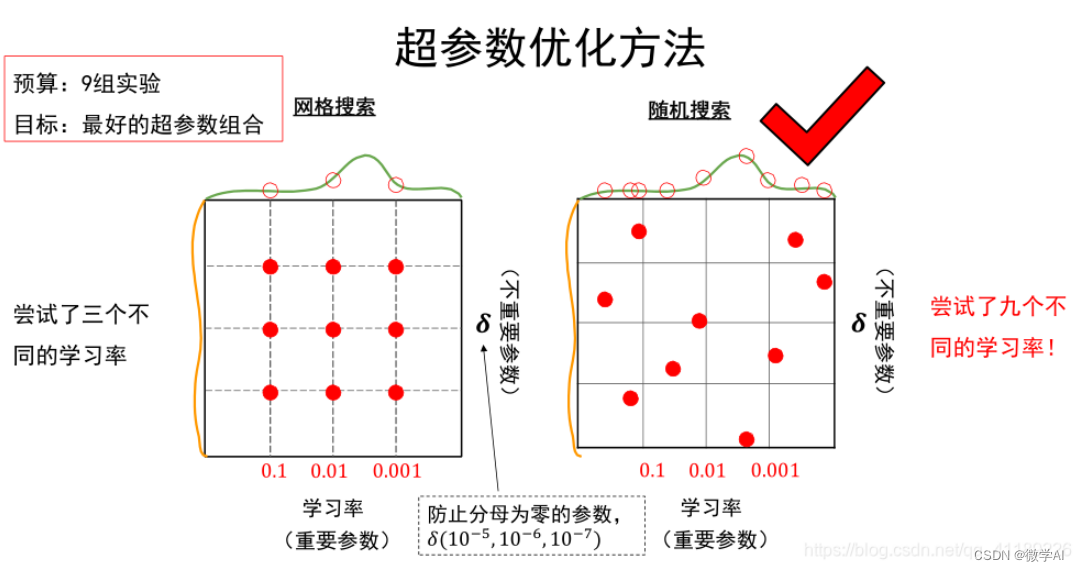
### 3.2.1 网格搜索与随机搜索

网格搜索（Grid Search）是评估超参数敏感性的基础方法之一，它通过穷举的方式遍历给定范围内的所有可能的超参数组合，评估每一组的性能指标。

**代码块示例：**

from sklearn.model_selection import GridSearchCV

param_grid = {
    'learning_rate': [0.01, 0.001, 0.0001],
    'batch_size': [32, 64, 128],
    'reg_lambda': [0.0, 0.1, 1.0]
}

grid_search = GridSearchCV(estimator=model, param_grid=param_grid, cv=5)
grid_search.fit(X_train, y_train)

此代码段展示了如何使用`GridSearchCV`对一个假设的深度学习模型进行网格搜索，其中`param_grid`定义了要搜索的超参数范围。

网格搜索虽然系统全面，但是当超参数数量较多或者参数的取值范围较大时，它需要的计算量可能成指数级增长。为了缓解这个问题，随机搜索（Random Search）被提出作为一种高效的替代方案。随机搜索不是遍历所有可能组合，而是在参数空间中随机选择组合进行评估，通常可以在较少的迭代次数内找到性能较好的模型。

### 3.2.2 基于贝叶斯优化的方法

贝叶斯优化是一种更高效的超参数调优方法，它使用贝叶斯模型来预测哪个超参数组合可能会带来最好的性能，然后有针对性地选择下一个要评估的超参数组合。

**代码块示例：**

from skopt import BayesSearchCV

bayes_search = BayesSearchCV(
    estimator=model,
    search_spaces=param_grid,
    n_iter=32,
    random_state=0
)
bayes_search.fit(X_train, y_train)

代码段使用`BayesSearchCV`进行贝叶斯优化，其中`n_iter`参数决定了优化过程中的迭代次数。

贝叶斯优化通常比网格搜索和随机搜索更快地收敛到最优解，尤其是在超参数空间很大且评估超参数组合的成本很高时。

### 3.2.3 梯度上升和遗传算法

梯度上升（Gradient