电路设计的创新解决方案:异或门与非门逻辑转换的全解析
发布时间: 2025-01-06 20:15:50 阅读量: 9 订阅数: 16 


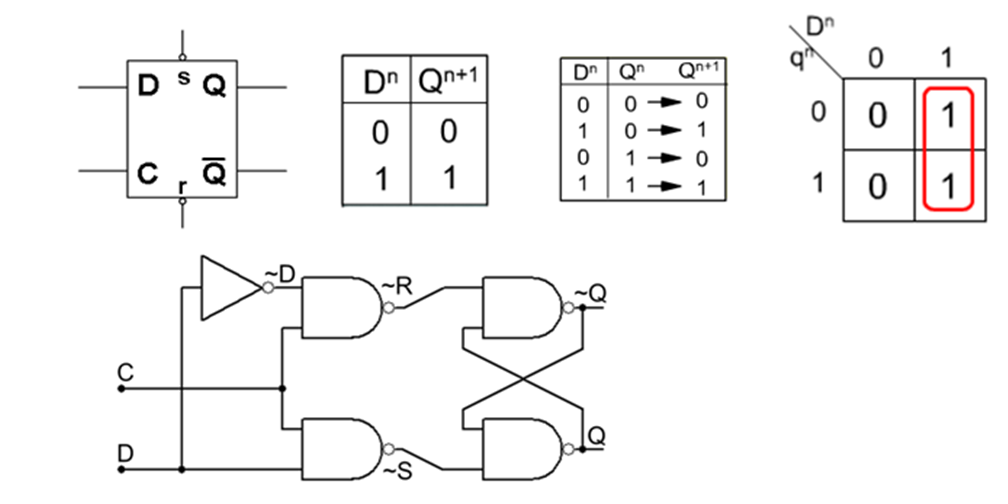
时序逻辑电路设计.docx
# 摘要
数字电路是电子工程领域的重要基础,其中逻辑门作为其基本构建块,具有核心作用。本文首先介绍了数字电路及逻辑门的基础知识,然后详细阐述了异或门与非门的工作原理及其在电路中的应用。在此基础上,本文进一步探讨了逻辑门之间的转换理论,并通过实际案例展示异或门与非门在电路设计中的应用。最后,本文展望了异或门与非门在现代电子技术中的创新应用,并预测了未来技术发展方向。研究成果不仅加深了对基本逻辑门的理解,也为逻辑门在复杂电路设计中的应用提供了理论和实践指导。
# 关键字
数字电路;逻辑门;异或门;非门;逻辑转换;电路设计
参考资源链接:[4个与非门构建异或逻辑](https://wenku.csdn.net/doc/3do5cfvxde?spm=1055.2635.3001.10343)
# 1. 数字电路基础与逻辑门简介
数字电路是电子技术的核心,它利用数字信号(0和1)来表示信息。逻辑门作为数字电路的基本构建块,负责执行布尔逻辑运算。在本章节中,我们将简要介绍数字电路的基本概念,并对逻辑门的功能和作用进行概述。为了更好地理解逻辑门,我们将从它的基本定义出发,探讨逻辑门在数字电路设计中的重要性,并为后续章节奠定基础。我们还将讨论为什么逻辑门是实现复杂数字系统不可或缺的基础组件。本章的内容为理解后续章节中涉及的具体逻辑门类型和它们的工作原理打下坚实基础。
# 2. 异或门与非门的基本工作原理
## 2.1 逻辑门的概念与分类
### 2.1.1 逻辑门定义及其在数字电路中的角色
逻辑门是数字电路的基础,是构建复杂电子系统的基石。它们可以实现基本的逻辑运算,如AND、OR和NOT等,是所有数字电路设计和计算过程中的最小逻辑单元。
数字电路可以被视作一种处理二进制信号的电路,它的信号只有两种状态,通常表示为0和1。逻辑门根据输入信号的不同组合,产生特定的输出。比如一个AND门,在两个输入都是1的情况下输出1,否则输出0。每个逻辑门都反映了某种特定的逻辑规则,这使得它们可以被串联和并联,构建出执行复杂操作的电路。
在数字电路中,逻辑门的作用不可或缺。它们不仅用于基本的逻辑运算,还能构建更复杂的函数电路,例如算术逻辑单元(ALU)、触发器、解码器等。逻辑门还可以被用来实现数据的存储和传输,对数据进行加密和解密,以及进行其他许多形式的信号处理。
### 2.1.2 异或门与非门的电路符号和逻辑功能
异或门(XOR)和非门(NOT)是两类最基本的逻辑门,它们各有独特的电路符号和逻辑功能。
非门,又被称为逻辑非门或反转门,它只有一个输入和一个输出。非门的唯一功能是反转输入信号:如果输入是1,输出就是0;如果输入是0,输出就是1。非门的电路符号通常是一个带有圆圈的小三角形,圆圈表示反转操作。在布尔代数中,非门的功能可以表示为Y = ¬A,其中A是输入,Y是输出,¬表示逻辑非运算。
异或门则稍微复杂一些,有两个输入和一个输出。异或门的输出在两个输入不同时为1,相同时为0。它的电路符号由三个输入输出端构成的圆形组成,带有一个斜线。在布尔代数中,异或门的功能可以表示为Y = A ⊕ B,其中A和B是输入,Y是输出,⊕代表异或运算。异或门可以实现简单的奇偶校验功能,还可以用于构建复杂的算术电路和数据转换电路。
## 2.2 异或门的工作原理
### 2.2.1 异或门的真值表和逻辑表达式
为了理解异或门的工作原理,我们首先需要查看它的真值表,真值表详细列出了所有可能输入组合下的输出结果。
下面是异或门的真值表:
| A (输入1) | B (输入2) | Y (输出) |
|-----------|-----------|----------|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
从真值表可以看出,只有当两个输入信号不一致时,输出才会是1;而当两个输入信号相同时,输出则是0。异或门的逻辑表达式可以表示为 Y = A ⊕ B。
### 2.2.2 异或门在电路中的实际应用
异或门在电路设计中非常有用,特别是在需要比较两个信号是否不同的场合。异或门在数据处理、错误检测与校验以及算术运算中都有广泛应用。
例如,在数据比较中,可以使用两个异或门来比较四位数字。如果所有相应的位都不相同,两个异或门的输出都会为1,通过一个后续的与门可以确定两个数字是否完全相异。
另一个例子是在奇偶校验位的生成中。在一些通信协议中,为了检测数据在传输过程中是否发生错误,会在数据的最后添加一个校验位,该位是数据中所有位的异或结果。如果数据位中包含偶数个1,则校验位为0;如果包含奇数个1,则校验位为1。接收方可以再次计算所有接收到的位的异或结果,若结果为0,则认为数据在传输过程中没有出错。
在算术运算中,异或门用于实现半加器和全加器的设计。半加器用于计算两个一位二进制数的和,它由一个异或门和一个与门组成。全加器则多了一个输入,可以用来计算三个一位二进制数的和,它包含了两个异或门、两个与门以及一个或门。
## 2.3 非门的工作原理
### 2.3.1 非门的真值表和逻辑表达式
非门的真值表非常简单,只有一个输入和一个输出,其输出始终是输入信号的逻辑非。以下是非门的真值表:
| A (输入) | Y (输出) |
|----------|----------|
| 0 | 1
0
0





