【CSP-S2数据结构与算法复赛精选题解】：深度剖析与实战应用技巧


# 摘要
本文全面介绍了CSP-S2复赛的关键知识点，重点阐述了数据结构和算法的深入解析及其应用。第一章为CSP-S2复赛概览与数据结构基础，第二章详细讨论了图论算法，并应用到实际案例中。第三章探讨了动态规划算法的策略与实现，强调了解题技巧。第四章分析了高级数据结构的实战应用，如Trie、AC自动机、线段树、树状数组和AVL Tree。第五章则专注于算法问题解决的思维模式，包括抽象思维、算法创新和时间管理。最后一章精选CSP-S2题目进行深入解析，讨论解题思路、算法与数据结构的融合，以及实战技巧。整体而言，本文旨在为读者提供一个全面的技术视角和解决复杂算法问题的策略。

# 关键字
CSP-S2复赛；数据结构；图论算法；动态规划；高级数据结构；算法思维

参考资源链接：[2020 CSP-J/S复赛题解与解析集锦](https://wenku.csdn.net/doc/5jt7bw5c0p?spm=1055.2635.3001.10343)
# 1. CSP-S2复赛概览与数据结构基础

## 1.1 CSP-S2复赛简介

中国计算机学会（CCF）举办的计算机软件能力认证（CSP-S2）复赛是中国IT行业的一项重要竞赛，它不仅考验了参赛者的编程能力，同时也检验了他们解决复杂问题的综合技能。复赛通常包含算法设计、数据结构应用、优化技巧等多个方面，要求参赛者具备扎实的计算机基础知识和快速编码实现的能力。

## 1.2 数据结构基础

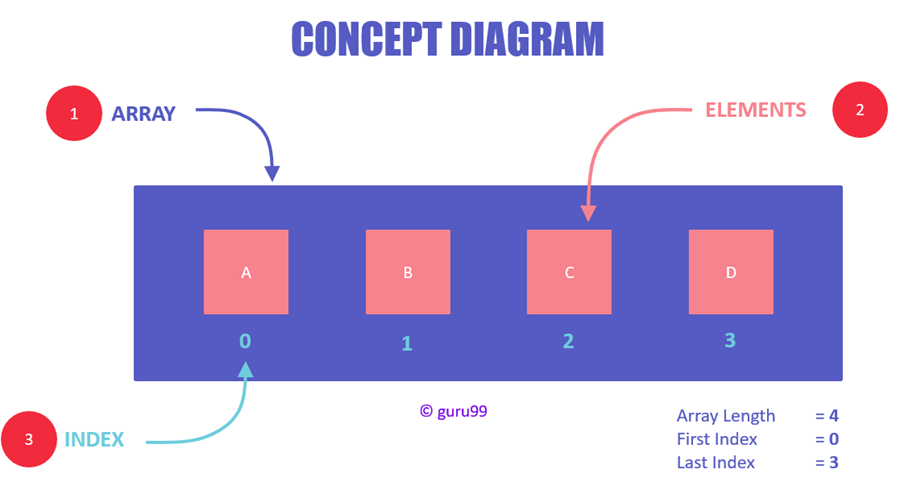
在准备CSP-S2复赛时，数据结构是基础中的基础。它涉及到如何高效地存储、管理和访问数据，是解决算法问题的基石。熟练掌握数组、链表、栈、队列、树、图等基本数据结构，对于解决算法问题至关重要。本章将重点回顾数据结构的基础知识，并为后续章节中更复杂的图论算法和动态规划算法打下坚实的基础。

## 1.3 数据结构学习路线

学习数据结构不能急于求成，需要按照以下步骤循序渐进：

- 理解每个数据结构的定义、特性和应用场景。
- 掌握基本操作，如插入、删除、查找等。
- 学习不同数据结构的高级操作和复杂算法。
- 通过解决具体问题来加深对数据结构使用的理解。
- 分析常见算法问题，如排序、搜索，以及它们与数据结构的关联。

在接下来的章节中，我们将深入探讨图论算法和动态规划算法，这两个领域通常在CSP-S2复赛中占有较大比重。通过大量的实例和实际题目的解析，我们将共同提升在这些领域的分析和解决能力。

# 2. 图论算法的深入解析与应用

### 2.1 图论基础知识回顾
图论是研究图的数学理论和应用的学科。图由顶点（vertices）和边（edges）组成，用来表示实体之间的某种特定关系。图可以分为有向图和无向图，分别表示为\( G = (V, E) \)，其中\( V \)是顶点集合，\( E \)是边集合。

#### 2.1.1 图的表示方法
图的表示方法主要有邻接矩阵和邻接表。邻接矩阵适用于边数量较少的稠密图，而邻接表适用于边数量较多的稀疏图。

1. **邻接矩阵**：用一个二维数组来表示图，其中\( adj[i][j] = 1 \)表示顶点\( i \)和顶点\( j \)之间有边，否则为0。
2. **邻接表**：通常用链表或数组实现，数组每个元素对应一个顶点，链表存储该顶点的所有邻接点。

#### 2.1.2 图的遍历算法
图的遍历算法主要有深度优先搜索（DFS）和广度优先搜索（BFS）。

1. **深度优先搜索（DFS）**：从一个顶点开始，尽可能深地搜索图的分支。
2. **广度优先搜索（BFS）**：从一个顶点开始，逐层向外扩展。

### 2.2 图的搜索算法详解
图的搜索算法用于在图中找到某点到另一点的路径或者是在无向图中寻找连通分量等。

#### 2.2.1 深度优先搜索（DFS）
DFS基于回溯的思想，使用递归或栈实现。

# Python代码示例
def dfs(graph, node, visited):
    if node not in visited:
        visited.add(node)
        print(node)  # 处理节点数据
        for neighbor in graph[node]:
            dfs(graph, neighbor, visited)

graph = {0: [1, 2], 1: [0, 3], 2: [0], 3: [1]}
visited = set()
dfs(graph, 0, visited)

在上述代码中，`graph` 是一个字典，表示图的邻接表形式。`dfs` 函数通过递归的方式实现深度优先遍历。每访问一个节点，就将其加入到`visited`集合中，确保每个节点只被访问一次。

#### 2.2.2 广度优先搜索（BFS）
BFS使用队列实现，从起点开始，逐层遍历图中的所有节点。

# Python代码示例
from collections import deque

def bfs(graph, start):
    visited = set()
    queue = deque([start])
    while queue:
        node = queue.popleft()
        if node not in visited:
            print(node)  # 处理节点数据
            visited.add(node)
            queue.extend(graph[node] - visited)  # 添加未访问的邻居节点到队列

graph = {0: [1, 2], 1: [0, 3], 2: [0], 3: [1]}
bfs(graph, 0)

在上述代码中，`bfs` 函数通过队列来控制遍历的顺序，确保从近到远地访问节点。

#### 2.2.3 应用案例分析
在解决实际问题时，图的搜索算法应用广泛，如迷宫问题、网络爬虫、社交网络分析等。

假设要解决一个简单的迷宫问题，可以用DFS来找到一条路径，或者用BFS来找到最短路径。

### 2.3 最短路径与网络流问题
最短路径问题是图论中一个经典问题，用于找到图中两节点之间的最短路径。网络流问题则是在网络中找到最大流量的路径。

#### 2.3.1 Dijkstra算法和Bellman-Ford算法
Dijkstra算法适用于没有负权边的图，可以找到单源最短路径。

# Python代码示例
import heapq

def dijkstra(graph, start):
    distances = {vertex: float('infinity') for vertex in graph}
    distances[start] = 0
    priority_queue = [(0, start)]

    while priority_queue:
        current_distance, current_vertex = heapq.heappop(priority_queue)
        if current_distance > distances[current_vertex]:
            continue
        for neighbor, weight in graph[current_vertex].items():
            distance = current_distance + weight
            if distance < distances[neighbor]:
                distances[neighbor] = distance
                heapq.heappush(priority_queue, (distance, neighbor))
    return distances

graph = {
    'A': {'B': 1, 'C': 4},
    'B': {'A': 1, 'C': 2, 'D': 5},
    'C': {'A': 4, 'B': 2, 'D': 1},
    'D': {'B': 5, 'C': 1}
}
print(dijkstra(graph, 'A'))

Dijkstra算法通过优先队列（最小堆）来优化搜索过程，从而降低时间复杂度。

Bellman-Ford算法则可以处理带有负权边的图，但它的时间复杂度较Dijkstra算法高。

#### 2.3.2 网络流基本概念与Ford-Fulkerson方法
网络流问题通过在网络中寻找最大流来解决。Ford-Fulkerson方法是寻找网络中最大流的一种方法，通过寻找增广路径来逐步增加流。

# 伪代码示例
def ford_fulkerson(graph, source, sink):
    residual_graph = create_residual_graph(graph)
    max_flow = 0

    while True:
        path = bfs(residual_graph, source, sink)
        if not path:
            break
        flow = find_min_capacity(path)
        max_flow += flow
        update_residula_graph(residual_graph, path, flow)
    return max_flow

上述伪代码中，`create_residual_graph` 创建残余网络，`bfs` 寻找增广路径，`find_min_capacity` 计算该路径上的最小容量，`update_residula_graph` 更新残余网络。

#### 2.3.3 题目实战演练
在实战演练中，可以结合实际问题，如社交网络中信息的传播、道路网络的交通规划等，应用最短路径和网络流算法解决问题。

### 结语
在深入理解图论的基础知识、搜索算法和最短路径以及网络流问题后，接下来的章节将探讨动态规划算法的策略与实现，并对高级数据结构的应用案例进行分析。

# 3. 动态规划算法的策略与实现

## 3.1 动态规划原理剖析

### 3.1.1 动态规划的概念和特点

动态规划是解决多阶段决策过程优化问题的一种数学方法，它将复杂问题拆分成相互关联的子问题，然后从最小子问题开始，逐步求解并储存子问题的解，以便于后续直接使用，避免重复计算。动态规划的特点是：问题可以分解为相互重叠的子问题，存在最优子结构（局部最优解能决定全局最优解），以及无后效性（子问题的解只与子问题的参数有关，与解决方案的步骤无关）。

动态规划常用于求解以下类型的问题：
- 计数问题（如求路径总数）
- 最值问题（如最大/小值问题）
- 存在性问题（是否能够达到某个状态）
- 构造性问题（构造出最终的解）

例如，在旅行推销员问题中，需要找到经过所有城市且总距离最短的路径。通过动态规划，可以将问题分解为寻找经过部分城市的最短路径问题，并构建一个解的表格来记录子问题的解。

### 3.1.2 状态转移方程的构建方法

构建状态转移方程是动态规划中最为关键的一步。一个有效的方法是将问题定义为状态，而状态之间的转移关系定义为状态转移方程。这通常需要根据问题的性质和已知条件，找到表示问题最优解的变量以及转移条件。

构建状态转移方程的一般步骤包括：
1. 定义状态：为每一个子问题定义一个或多个状态变量来表示子问题的解。
2. 确定状态转移方程：找到当前状态与子状态之间的关系，也就是如何从前一状态或多个状态得到当前状态。
3. 边界条件：确定状态转移方程的基础情况，即递归的终止条件。
4. 计算顺序：确定状态计算的顺序，即如何通过计算子状态来得到当前状态。

例如，对于背包问题，可以定义状态`dp[i][w]`表示考虑前`i`件物品，当前背包容量为`w`时能够装入的最大价值。状态转移方程则根据是否将第`i`件物品加入背包而分为两种情况。

## 3.2 动态规划问题的分类与解法

### 3.2.1 背包问题系列

背包问题可以分为以下几种：
- 0-1背包问题：每种物品只能使用一次。
- 完全背包问题：每种物品可以无限次使用。
- 多重背包问题：每种物品的数量有限。
- 分组背包问题：物