【Java编码到字节码】：打造可优化代码结构的10大秘诀

# 1. Java编码到字节码的转换过程

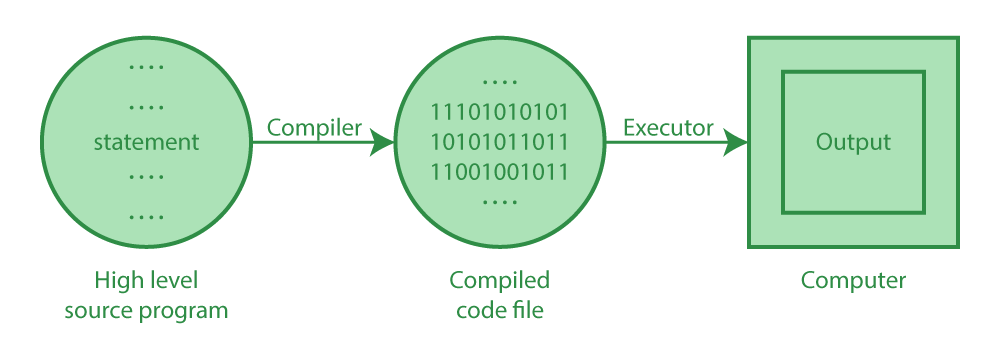
Java源代码通过编译器被转换为字节码是Java虚拟机（JVM）的核心能力之一。这一过程不仅涉及到语言本身的语法规则和结构，还包括了对代码的优化和安全检查。本章将介绍这一转换过程的基础知识，以及背后的概念和技术。

## 1.1 Java编译器的作用
Java编译器（javac）是负责将Java源代码转换为字节码的工具。源代码文件（.java）在经过编译后会生成一个或多个.class文件，每个文件都包含了对应源文件中类的字节码表示。

## 1.2 编译过程的步骤
这个过程大致分为两个步骤：首先是将源代码分解成一个个的词法单元（Token），然后是将这些单元组织成语法树（AST），最后编译为字节码。编译器还会进行类型检查和一些基本的优化。

## 1.3 字节码的特性
Java字节码是一种中间表示形式，具有平台无关性，这意味着相同的字节码文件可以在任何安装了Java虚拟机的系统上运行。字节码指令集合被设计为便于JVM快速执行，同时保持代码紧凑。

// 示例代码，Java源码
public class HelloWorld {
    public static void main(String[] args) {
        System.out.println("Hello, World!");
    }
}

编译后的字节码指令示例（部分展示）：

  public static void main(java.lang.String[]);
    descriptor: ([Ljava/lang/String;)V
    flags: ACC_PUBLIC, ACC_STATIC
    Code:
      stack=2, locals=1, args_size=1
         0: getstatic     #2                  // Field java/lang/System.out:Ljava/io/PrintStream;
         3: ldc           #3                  // String Hello, World!
         5: invokevirtual #4                  // Method java/io/PrintStream.println:(Ljava/lang/String;)V
         8: return
      LineNumberTable:
        line 3: 0
        line 4: 8
      LocalVariableTable:
        Start  Length  Slot  Name   Signature
            0       9     0  args   [Ljava/lang/String;

通过以上示例，我们可以了解到Java编译器在将源代码转换为字节码时的具体操作步骤，以及生成的字节码的基本结构。这一过程是Java运行时环境的基础，也是深入理解Java性能优化的关键起点。

# 2. ```
# 第二章：理解Java字节码

## 2.1 字节码基础

### 2.1.1 字节码与Java虚拟机(JVM)

Java字节码是Java源代码经过编译后生成的指令集合，它被设计为能够被Java虚拟机（JVM）理解并执行。JVM是一个抽象的计算机，它模拟了一台物理机器的行为，使得Java程序能够在不同的操作系统和硬件架构上运行，而无需重新编译。字节码是JVM的语言，Java程序一旦编译成字节码，就可以通过JVM在任何平台上运行，这个特性被称为“一次编写，到处运行”。

字节码文件通常以`.class`扩展名存在于Java项目中。JVM加载字节码文件并将其转换成对应操作系统的机器代码，然后执行。这种转换机制包括了JIT（Just-In-Time）编译，它在运行时将热点代码编译成本地机器码，以提升执行速度。

### 2.1.2 字节码文件结构

字节码文件是Java类的二进制表示，它包含了一系列指令和符号信息。一个典型的字节码文件结构可以分为以下几个部分：

- 魔数（Magic Number）：文件的第一个4个字节，用于确定文件是否是有效的Java类文件。
- 版本号：接下来的4个字节指明了Java类文件的版本，包括次版本号和主版本号。
- 常量池：紧接着版本信息后面的是常量池入口，常量池包含了一系列的字面量和符号引用信息。
- 访问标志：接下来两个字节定义了类或接口的访问权限和属性。
- 类索引、父类索引和接口索引集合：这些信息用于确定类的继承关系。
- 字段表、方法表和属性表：这些表包含了类中定义的所有字段、方法和类级别的属性信息。

// 示例：简单的Java类
public class HelloWorld {
  public static void main(String[] args) {
    System.out.println("Hello, World!");
  }
}

对应于上述Java代码的简单示例字节码指令可能包含如下操作：

public class HelloWorld
  minor version: 0
  major version: 52
  flags: ACC_PUBLIC, ACC_SUPER
// 类常量池入口
Constant pool:
   #1 = Methodref          #4.#18        // java/lang/Object."<init>":()V
   #2 = Fieldref           #3.#19        // HelloWorld.out:Ljava/io/PrintStream;
   #3 = Class              #20           // HelloWorld
   #4 = Class              #21           // java/lang/Object
   #5 = String             #22           // Hello, World!
   #6 = Methodref          #23.#24       // java/io/PrintStream.println:(Ljava/lang/String;)V
   #7 = Class              #25           // java/io/PrintStream
// ...
// main方法的字节码指令
public static void main(java.lang.String[]);
  descriptor: ([Ljava/lang/String;)V
  flags: ACC_PUBLIC, ACC_STATIC
  Code:
    stack=2, locals=1, args_size=1
       0: getstatic     #2                  // Field out:Ljava/io/PrintStream;
       3: ldc           #5                  // String Hello, World!
       5: invokevirtual #6                  // Method java/io/PrintStream.println:(Ljava/lang/String;)V
       8: return
    LineNumberTable:
      line 1: 0
      line 2: 8

这个简单的示例字节码文件包含了一个主方法，该方法向控制台打印出一条消息。字节码指令在JVM上执行，完成该Java程序的运行。

## 2.2 字节码与Java类文件

### 2.2.1 类文件的加载与验证

当JVM开始执行一个Java程序时，它会按照需要加载和链接必要的类文件。类的加载涉及到读取类文件并解析其中的二进制数据，这个过程包括验证、准备、解析三个步骤：

- 验证（Verification）：确保类文件的结构正确且符合JVM规范，包括校验魔数、版本号、字节码指令等。
- 准备（Preparation）：为类变量分配内存并设置类变量的默认初始值。
- 解析（Resolution）：将类、接口、字段和方法的符号引用转换为直接引用。

// 示例：简单的Java类加载和验证过程
// 该代码执行类加载和验证的简化操作
public class ClassLoaderExample {
  public static void main(String[] args) {
    try {
      Class<?> clazz = Class.forName("HelloWorld");
      System.out.println("Loaded class: " + clazz.getName());
    } catch (ClassNotFoundException e) {
      System.err.println("Class not found.");
    }
  }
}

### 2.2.2 类与方法的字节码指令

类文件中包含了类的定义和各种方法的字节码指令。每个方法都有一系列的字节码指令，它们按照一定顺序排列，用于完成方法体中指定的功能。

// 示例：某个方法的字节码指令
public void exampleMethod() {
  // 方法体
}

对应的字节码指令可能如下：

public void exampleMethod();
  descriptor: ()V
  flags: ACC_PUBLIC
  Code:
    stack=1, locals=1, args_size=1
       0: return
    LineNumberTable:
      line 5: 0

这段代码表示一个没有任何实际操作的空方法。在字节码中，`0: return`表示方法返回，且没有使用任何栈帧空间（stack=1）。

## 2.3 字节码的动态生成与修改

### 2.3.1 动态代理与字节码操作库

在Java中，动态代理是一种编程技术，它允许在运行时动态地创建接口的实现对象。动态代理通常用于实现AOP（面向切面编程）等技术，能够增强或改变对象的行为。实现动态代理的一个核心组件是字节码操作库，如ASM或CGLIB。这些库提供了直接操作字节码的能力，允许开发者在不修改源代码的情况下生成新的类。

字节码操作库通常包含以下功能：

- 分析现有类文件
- 动态创建和修改类文件
- 注册和管理生成的类

// 示例：使用CGLIB库创建动态代理类
Enhancer enhancer = new Enhancer();
enhancer.setSuperclass(HelloWorld.class);
enhancer.setCallback((MethodInterceptor) (obj, method, args, proxy) -> {
  System.out.println("Before method call");
  Object result = proxy.invokeSuper(obj, args);
  System.out.println("After method call");
  return result;
});
HelloWorld proxyInstance = (HelloWorld) enhancer.create();

### 2.3.2 字节码注入与框架实现

字节码注入是一种向目标类中插入新的代码片段的技术，它被广泛应用于框架开发中。通过字节码注入，框架可以在运行时修改类的行为，而不需要改变原始代码。常见框架如Spring AOP、Hibernate等内部使用了字节码技术来实现各种功能。

例如，在Spring框架中，可以通过