傅里叶变换在深度学习中的应用大揭秘：从图像分类到自然语言处理，让AI更智能

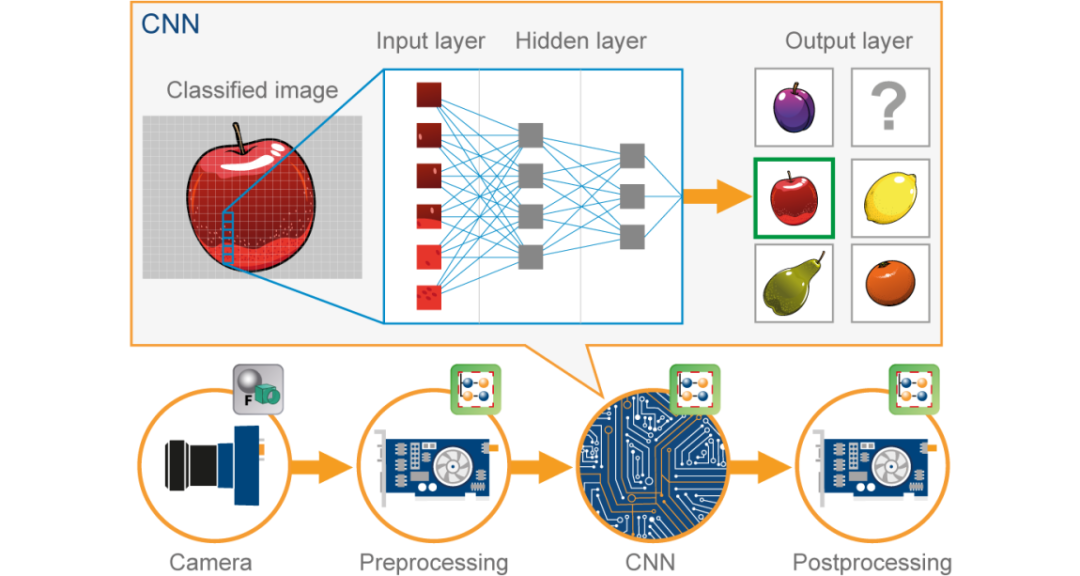
# 1. 傅里叶变换的基础理论

傅里叶变换是一种数学工具，用于将时域信号分解为频率域信号。它揭示了信号中不同频率分量的幅度和相位信息。

傅里叶变换的数学表达式为：

F(ω) = ∫_{-\infty}^{\infty} f(t) e^(-iωt) dt

其中：

* `f(t)` 是时域信号
* `F(ω)` 是频率域信号
* `ω` 是角频率

傅里叶变换具有线性、可逆和卷积等重要性质，使其在信号处理和分析中广泛应用。

# 2. 傅里叶变换在深度学习中的应用原理

### 2.1 图像分类中的傅里叶变换

#### 2.1.1 图像频谱分析

图像频谱分析是将图像表示为其频率分量的过程。傅里叶变换是一种数学工具，可以将图像从时域（像素值）转换为频域（频率分量）。

**代码块：**

import numpy as np
import cv2

# 读取图像
image = cv2.imread('image.jpg')

# 傅里叶变换
dft = cv2.dft(image, flags=cv2.DFT_COMPLEX_OUTPUT)

# 移位零频率分量到图像中心
dft_shift = np.fft.fftshift(dft)

# 计算幅度谱
magnitude_spectrum = 20 * np.log(cv2.magnitude(dft_shift[:, :, 0], dft_shift[:, :, 1]))

**逻辑分析：**

* `cv2.dft()` 函数执行傅里叶变换，生成复数输出，其中实部和虚部分别表示图像的幅度谱和相位谱。
* `np.fft.fftshift()` 函数将零频率分量移到图像中心，便于可视化。
* `cv2.magnitude()` 函数计算幅度谱，表示每个频率分量的强度。

#### 2.1.2 卷积神经网络中的傅里叶变换

卷积神经网络（CNN）是一种深度学习模型，广泛用于图像分类。傅里叶变换可以帮助理解 CNN 的工作原理。

**代码块：**

import tensorflow as tf

# 定义卷积层
conv_layer = tf.keras.layers.Conv2D(32, (3, 3), activation='relu')

# 获取卷积核权重
weights = conv_layer.get_weights()[0]

# 计算卷积核的频谱
weights_fft = np.fft.fft2(weights)

**逻辑分析：**

* CNN 的卷积操作本质上是图像与卷积核的乘积和。
* 傅里叶变换可以将卷积核分解为其频率分量。
* 分析卷积核的频谱可以揭示其对不同频率图像特征的敏感性。

### 2.2 自然语言处理中的傅里叶变换

#### 2.2.1 文本频谱分析

文本频谱分析是将文本表示为其频率分量的过程。傅里叶变换可以将文本从时域（单词序列）转换为频域（频率分量）。

**代码块：**

import numpy as np
from sklearn.feature_extraction.text import CountVectorizer

# 提取文本特征
vectorizer = CountVectorizer()
X = vectorizer.fit_transform(['sentence 1', 'sentence 2', 'sentence 3'])

# 傅里叶变换
X_fft = np.fft.fft(X)

**逻辑分析：**

* `CountVectorizer()` 函数将文本转换为词频矩阵，其中每个单词是一个特征。
* 傅里叶变换将词频矩阵转换为频域，揭示了文本中单词共现的频率模式。

#### 2.2.2 循环神经网络中的傅里叶变换

循环神经网络（RNN）是一种深度学习模型，广泛用于自然语言处理。傅里叶变换可以帮助理解 RNN 的时间依赖性。

**代码块：**

import tensorflow as tf

# 定义循环层
rnn_layer = tf.keras.layers.LSTM(128)

# 获取循环层的权重
weights = rnn_layer.get_weights()[0]

# 计算循环层的频谱
weights_fft = np.fft.fft(weights)

**逻辑分析：**

* RNN 的循环操作本质上是前一时间步状态与当前时间步输入的乘积和。
* 傅里叶变换可以将循环层的权重分解为其频率分量。
* 分析循环层的频谱可以揭示其对不同时间尺度输入的敏感性。

# 3. 傅里叶变换在深度学习中的实践案例

### 3.1 图像分类中的傅里叶变换应用

#### 3.1.1 图像去噪和增强

傅里叶变换在图像去噪和增强中发挥着至关重要的作用。通过将图像转换为频域，我们可以有效地分离噪声和图像信号。

import numpy as np
import cv2
import matplotlib.pyplot as plt

# 读取图像
image = cv2.imread('noisy_image.jpg')

# 傅里叶变换
dft = cv2.dft(np.float32(image), flags=cv2.DFT_COMPLEX_OUTPUT)
dft_shift = np.fft.fftshift(dft)

# 创建一个掩码来过滤高频噪声
mask = np.zeros((dft_shift.shape[0], dft_shift.shape[1]), np.uint8)
mask[dft_shift.shape[0]//2-50:dft_shift.shape[0]//2+50, dft_shift.shape[1]//2-50:dft_shift.shape[1]//2+50] = 1

# 应用掩码
filtered