递归与迭代：疫情模拟中效率与精准度的比较


参考资源链接：[递归算法求解传染病问题](https://wenku.csdn.net/doc/6412b75bbe7fbd1778d4a00d?spm=1055.2635.3001.10343)
# 1. 递归与迭代概念解析

在计算机科学中，递归和迭代是两种基础且常见的算法设计模式。尽管它们都能解决同样的问题，但它们在逻辑结构、效率和实现方式上存在着明显的差异。理解这两种模式，对于编写高效、优雅的代码至关重要。

## 递归的基本概念

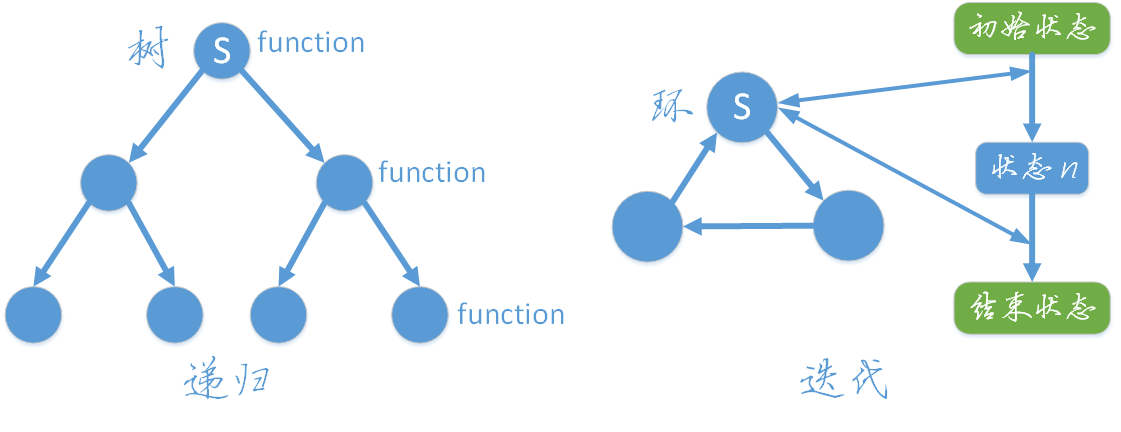
递归是一种问题解决方法，其中函数调用自身来解决问题的子问题。递归函数通常包含两个主要部分：基本情况（base case）和递归步骤（recursive case）。基本情况是递归结束的条件，而递归步骤则是缩小问题规模并继续递归的过程。递归函数的每次调用都创建一个新的函数实例，这可能导致较大的内存开销。

## 迭代的基本概念

迭代则是通过循环结构（如for或while循环）重复执行一组指令来解决问题。与递归不同，迭代不会创建新的函数调用栈，因此通常内存效率更高。迭代方法更依赖于循环条件和迭代过程中的变量状态更新。

递归和迭代在实际应用中各有优势。递归的代码通常更简洁，易于理解，特别适用于树形或图的遍历等问题。而迭代则更适合解决简单的线性问题，并且可以避免递归可能引起的栈溢出问题。选择使用递归还是迭代，往往取决于具体问题的性质和对性能的考虑。

# 2. 理论基础与疫情模型构建

## 2.1 递归的理论基础

### 2.1.1 递归的工作原理

递归是计算机科学中一种强大的算法设计技巧，其核心思想在于将一个复杂的问题分解为若干个更小、更易于解决的相似问题。在解决这些问题时，递归方法会反复调用自身，直到达到一个基准情形（base case），这个基准情形是不需要递归就可以直接解决的简单问题。递归通过“分而治之”的原则，使得复杂的算法问题变得可解。

递归函数通常具有以下三个重要特征：
1. **基准情形（Base Case）**：递归停止的条件，防止无限递归。
2. **递归情形（Recursive Case）**：函数调用自身来处理子问题的步骤。
3. **递归关系**：问题分解的规则，确定如何通过组合子问题的解来构造原问题的解。

### 2.1.2 递归在疫情模型中的应用

在疫情模型中，递归可以用来模拟病毒传播的连锁反应。例如，通过递归算法可以计算出在给定的感染率和接触模式下，一个感染者在特定时间内可能传染给多少人。递归模型可以构建出病毒传播的树状结构，展示每个感染者如何成为新的感染源。

def calculate_new_infections(current_infections, days, infection_rate):
    """
    递归计算未来几天内的新感染人数。
    :param current_infections: 当前感染人数
    :param days: 计算的天数
    :param infection_rate: 感染率
    :return: 新增感染人数列表
    """
    if days <= 0:
        return []
    new_infections = current_infections * infection_rate
    return [int(new_infections)] + calculate_new_infections(new_infections, days - 1, infection_rate)

# 示例：当前有10个感染者，每天感染率为10%，计算未来3天的感染人数
infections = calculate_new_infections(10, 3, 0.10)
print(infections)

在这个示例中，`calculate_new_infections` 函数展示了如何使用递归计算接下来几天内可能出现的新感染人数。每次递归调用都会计算出一天后的新感染人数，并将其添加到列表中。

## 2.2 迭代的理论基础

### 2.2.1 迭代的工作原理

与递归不同，迭代是通过重复应用相同的处理过程来逐步逼近问题解决方案的方法。迭代通常使用循环结构来实现，如for循环和while循环。迭代的优点在于它不需要额外的系统调用栈空间，因此通常比递归实现占用更少的内存空间，并且避免了递归可能导致的栈溢出问题。

迭代过程通常由以下步骤构成：
1. 初始化变量或数据结构。
2. 在满足循环条件的前提下，重复执行循环体内的操作。
3. 更新循环条件所依赖的变量。
4. 当循环条件不再满足时，退出循环。

### 2.2.2 迭代在疫情模型中的应用

在构建疫情模型时，迭代方法可以用来模拟每日新增感染数的变化。例如，可以使用迭代方法来预测接下来几天内，根据当前的感染率和治愈率，每天的新增和减少的感染人数。

def iterative_infection_simulation(initial_infected, days, infection_rate, recovery_rate):
    """
    迭代模拟疫情发展。
    :param initial_infected: 初始感染人数
    :param days: 模拟的天数
    :param infection_rate: 感染率
    :param recovery_rate: 治愈率
    :return: 每天的感染人数列表
    """
    infections = [initial_infected]
    for _ in range(days - 1):
        new_infections = infections[-1] * infection_rate
        recoveries = infections[-1] * recovery_rate
        infections.append(new_infections - recoveries)
    return infections

# 示例：初始感染人数为50，模拟10天，感染率为20%，治愈率为5%
infection_simulation = iterative_infection_simulation(50, 10, 0.20, 0.05)
print(infection_simulation)

在这个示例中，函数`iterative_infection_simulation`使用了迭代方法来预测疫情的发展趋势。通过模拟每天的新增和减少的感染人数，可以得到一个时间序列，描述了疫情的变化过程。

## 2.3 疫情模型的构建

### 2.3.1 SIR模型简介

SIR模型是描述传染病在人群中传播的一种经典模型。该模型将人群分为三类：易感者（Susceptible），即尚未感染但有感染风险的人群；感染者（Infected），即当前已经被感染的人群；移除者（Recovered），即已经康复并获得免疫力的人群。

- **S(t)**：时间t的易感者数量。
- **I(t)**：时间t的感染者数量。
- **R(t)**：时间t的移除者数量。
根据经典的SIR模型，每天的感染者数量变化可以表示为：

dI/dt = β * I(t) * S(t) / N - γ * I(t)

其中，β为感染率，γ为康复率。

### 2.3.2 疫情模型参数设定

为了建立一个实用的疫情模型，我们必须设定合理的参数。参数通常包括感染率、康复率、初始的感染者数量以及人群的总数。模型的准确性在很大程度上取决于这些参数是否能够反映真实世界中的疫情状态。

例如，如果我们设定一个地区的人口总数为100万，初始感染者为100人，感染率为20%，康复率为5%，我们可以使用上述的SIR模型来模拟疫情的发展。

flowchart LR
    S(Suscepti