NIST随机数算法原理深度剖析：数学基础与实现细节


参考资源链接：[NIST随机数测试标准中文详解及16种检测方法](https://wenku.csdn.net/doc/1cxw8fybe9?spm=1055.2635.3001.10343)
# 1. NIST随机数算法的背景与重要性

在现代信息安全领域中，随机数算法的背景和重要性不容忽视。美国国家标准与技术研究院（NIST）提出的随机数算法为众多信息安全应用提供了坚实的理论基础和实践指导。这不仅仅是因为随机数广泛应用于密码学和安全通信领域，更是因为随机数的不可预测性和均匀分布性是保障数字安全的关键要素。本章我们将探讨NIST随机数算法的起源、其在不同技术领域的重要性，以及在当前信息安全领域所扮演的核心角色。这将为我们后续深入了解NIST算法的技术细节和应用案例打下坚实基础。

# 2. 随机数生成的数学基础

### 2.1 随机数的分类与特性

#### 2.1.1 真随机数与伪随机数

在密码学和信息安全领域，随机数扮演着核心的角色。它们被用来生成密钥、初始化向量、盐值等，是构建安全系统不可或缺的组成部分。随机数可以根据其产生的本质属性被分为两类：真随机数（True Random Numbers）和伪随机数（Pseudorandom Numbers）。

真随机数是由物理过程或物理现象产生的，它们的产生不依赖于任何算法。例如，通过测量放射性原子核的衰变事件、热噪声或量子现象来生成的随机数被认为是真随机数。真随机数的不可预测性和不可重现性是它们的最大特点，这使它们在安全性要求极高的场合中成为首选。

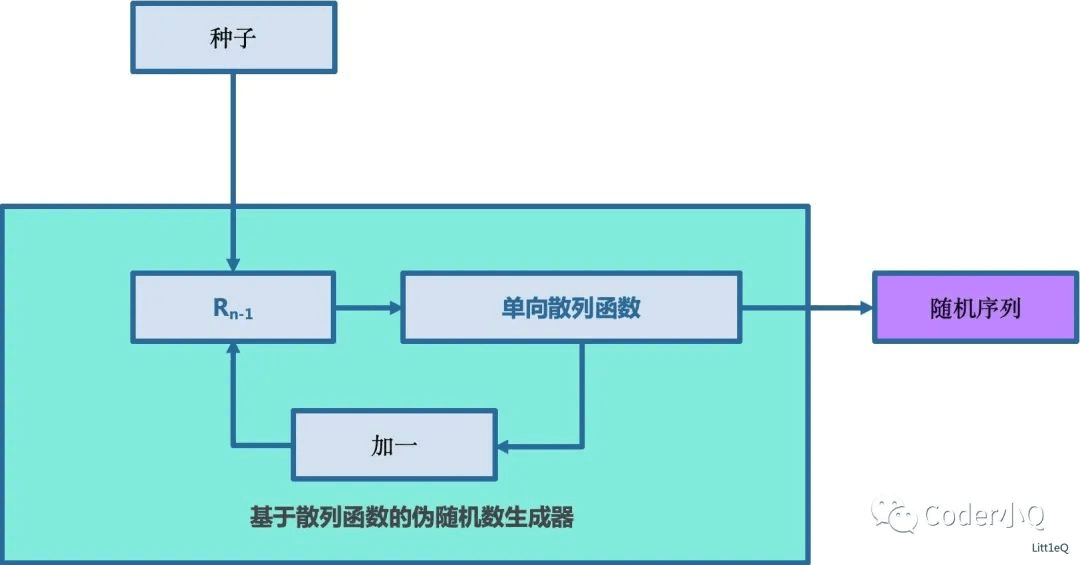
伪随机数则不同，它们由确定性算法生成。尽管这些算法可以产生序列，从统计上看起来很随机，但它们是完全可预测的，只要知道种子值和算法本身。这意味着如果伪随机数生成器的内部状态被泄露，那么生成的所有随机数序列就不再安全。然而，由于伪随机数生成器具有快速、高效的特点，它们在许多应用中仍然非常流行。

#### 2.1.2 随机数的统计特性

随机数的统计特性是指随机数序列中数字分布的统计规律。理想情况下，随机数应该均匀分布，即每个数字在0到1之间出现的概率应该相等。然而，由于各种算法的差异和物理实现的限制，现实中生成的随机数往往难以达到完美均匀。

在随机数的统计测试中，常见的几个特性包括：

- **均匀性**：每个数字出现的概率应该相同。
- **独立性**：任意两个数字之间的出现应该是独立的，不存在统计相关性。
- **不可预测性**：下一个数字的出现应该是不可预测的。

### 2.2 密码学中的随机数要求

#### 2.2.1 随机数的不可预测性

密码学应用要求生成的随机数必须具有很高的不可预测性。在加密算法中，随机数用作密钥或初始化向量，这些值如果可预测，那么加密过程就有可能被破解。为了达到不可预测的要求，现代密码学中使用的随机数生成器通常是基于硬件的真随机数生成器，或者是高级的伪随机数生成器，它们使用复杂的算法来确保不可预测性。

#### 2.2.2 随机数的均匀分布性

均匀分布性对于确保密码学算法的强度至关重要。如果随机数分布不均，那么某些数字序列可能会被过于频繁地使用，这会减少密钥空间的实际大小，从而降低加密系统的安全性。举例来说，在密钥生成中，如果某个特定的值生成的概率比其他值要高，那么密钥的强度就会降低，因为攻击者可以利用这一点来集中破解。

### 2.3 随机数生成的数学原理

#### 2.3.1 概率论基础

概率论是数学的一个分支，它研究随机事件及其发生的概率。随机数生成的原理基于概率论中的随机变量和随机过程。一个随机变量是一个变量，其值由随机现象的结果决定。而随机过程则是指一系列的随机变量构成的序列。

在随机数生成的过程中，我们关注的是均匀随机变量，即每个可能结果出现的概率都相等的随机变量。通过选择合适的数学模型和概率分布，我们可以确保生成的随机数序列在统计上达到理想的均匀性。

#### 2.3.2 随机过程与随机变量

随机过程是随机变量按照时间顺序排列的集合，它可以被看作是一个随机的"动态系统"。在密码学中，常见的随机过程包括线性同余生成器、线性反馈移位寄存器（LFSR）等。这些过程产生的随机数序列可以通过特定的数学公式进行描述。

随机变量是随机过程中的一个概念，它表示可能的结果。在随机数生成中，我们通常希望随机变量具有特定的概率分布，比如均匀分布或正态分布。通过精心设计的数学公式和参数选择，我们可以使生成的随机数序列尽可能地接近理论上的分布。

随机数生成器在实际应用中需要具备高性能和高安全性。因此，深入理解这些数学原理对于开发、评估和使用随机数生成器至关重要。在下一章，我们将探讨NIST随机数算法的技术细节，并深入了解其如何实现这些数学原理。

# 3. NIST随机数算法的技术细节

## 3.1 NIST算法概述

### 3.1.1 算法的设计理念

NIST随机数算法的设计理念侧重于提供高质量、可重现的随机数序列，以满足现代密码学中对随机性的严格要求。这些算法通过使用一系列精心挑选的数学函数和变换，确保生成的随