机器学习中的概率密度估计：核密度估计与高斯混合模型的实用技巧


# 摘要
本文首先介绍了概率密度估计的基础知识，随后详细阐述了核密度估计和高斯混合模型的理论与应用。核密度估计部分重点讲解了其基本概念、核函数的选择、带宽选择的重要性以及在实际中的应用技巧。高斯混合模型章节则从模型简介出发，覆盖了参数估计、评估与选择方法，并探讨了其在数据聚类中的应用。两者的比较与实践应用分析了它们在密度估计中的优势与局限，提出了选择和结合两者的策略，并探讨了性能优化技巧。最后，通过金融数据、生物信息学数据以及社交媒体行为的案例研究，展示了所讨论技术在实际问题中的应用与效果。

# 关键字
概率密度估计；核密度估计；高斯混合模型；核函数；带宽选择；数据聚类

参考资源链接：[概率视角下的机器学习：深度解析与实践探索](https://wenku.csdn.net/doc/6412b67fbe7fbd1778d46eff?spm=1055.2635.3001.10343)
# 1. 概率密度估计基础

在统计学和机器学习中，概率密度估计是一项基础而重要的任务，它致力于根据有限的样本数据推断出总体的概率分布特征。本章将首先介绍概率密度估计的基本概念及其重要性，并为理解后续章节中核密度估计和高斯混合模型打下坚实的基础。

## 1.1 概率密度估计的重要性

概率密度函数（Probability Density Function, PDF）对于理解随机变量的行为至关重要。PDF 描述了变量取某个值或落在某个区间内的概率密度。在实际应用中，往往需要估计这个分布，特别是在数据样本有限的情况下。正确的概率密度估计能帮助我们更好地进行预测、分类和决策。

## 1.2 概率密度估计的方法

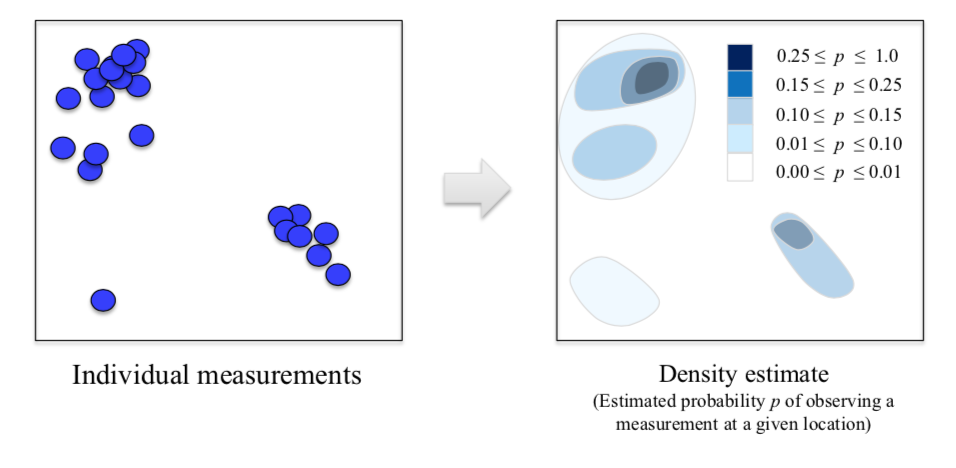
概率密度估计的方法多种多样，包括直方图法、核密度估计法和参数估计方法等。直方图法简单直观，但依赖于区间的选择；核密度估计克服了直方图的一些局限性，提供了一种更平滑的估计方式；而参数估计方法则需要假定数据符合某个分布模型。在这一章节中，我们将重点介绍核密度估计，因为它在现实世界中的应用更为广泛且效果显著。

# 2. 核密度估计的理论与应用

核密度估计（Kernel Density Estimation，简称KDE）是一种用于估计概率密度函数的非参数方法。它通过在每个数据点附近放置一个核函数，然后将这些核函数叠加起来形成整个数据集的概率密度估计。核密度估计在许多领域，如统计学、机器学习、信号处理和数据分析中都得到了广泛应用。

## 2.1 核密度估计的基本概念

### 2.1.1 概率密度函数的重要性

在概率论和统计学中，概率密度函数（Probability Density Function，简称PDF）对于描述连续随机变量的分布至关重要。PDF可以告诉我们某个值在多大程度上是可能的，但它不直接给出随机变量取特定值的概率。取而代之，概率密度函数允许我们计算随机变量落在某个区间内的概率。概率密度估计则是寻找一个连续的概率密度函数，最准确地反映数据集中的分布。

### 2.1.2 核密度估计的定义和原理

核密度估计是一种非参数估计方法，其核心思想是在每个数据点周围放置一个核函数（kernel function），常见的核函数包括高斯核、Epanechnikov核等。核函数的选择决定了密度估计的平滑程度和形状。通过将这些核函数在数据点处叠加，我们可以得到数据集的概率密度估计。

核密度估计的公式可以表示为：
\[ f(x) = \frac{1}{n}\sum_{i=1}^{n}K_h(x-x_i) \]
其中，\( f(x) \) 是概率密度函数的估计值，\( n \) 是样本数量，\( x_i \) 是数据点，\( K_h \) 是带有带宽参数 \( h \) 的核函数，它负责调节每个数据点对密度估计的影响。

## 2.2 核函数的选择与应用

### 2.2.1 常见核函数的特性对比

不同的核函数会影响核密度估计的结果，因此选择合适的核函数非常重要。下面列出一些常见的核函数及其特性：

| 核函数名称 | 公式 | 特性 |
| --- | --- | --- |
| 高斯核 | \( K(u) = \frac{1}{\sqrt{2\pi}} e^{-\frac{u^2}{2}} \) | 形状接近正态分布，对异常值不敏感。 |
| Epanechnikov核 | \( K(u) = \frac{3}{4}(1-u^2), |u|\leq 1 \) | 最优的均方误差特性。 |
| 矩形核 | \( K(u) = \frac{1}{2} \) | 计算简单，但边界效应明显。 |
| 三角核 | \( K(u) = \frac{3}{4}(1-|u|), |u|\leq 1 \) | 介于矩形核和Epanechnikov核之间。 |

### 2.2.2 如何选择合适的核函数

选择核函数时需要考虑数据的特性以及密度估计的目的。一般来说，高斯核是应用最广泛的选择，因为它对异常值的鲁棒性较好，且数学性质较为稳定。Epanechnikov核在理论上是最优的，但在实际中使用较少，因为其导数在边界处不连续。矩形核计算简单，但边缘效应过于明显，而三角核则是在矩形核和Epanechnikov核之间的一个折中选择。

## 2.3 核密度估计的带宽选择

### 2.3.1 带宽的理论基础

带宽（bandwidth）是核密度估计中非常重要的一个超参数，决定了每个核函数的宽度。带宽的选择直接影响到密度估计的平滑程度。如果带宽太小，密度估计会出现很多“峰值”，对噪声过度敏感；如果带宽太大，密度估计又会过于平滑，可能掩盖真实的分布特征。

### 2.3.2 实践中带宽选择的策略

带宽的选择策略可以分为两类：经验规则和交叉验证方法。

经验规则中最常用的是Silverman规则：
\[ h = \min\left\{ \sigma, \frac{IQR}{1.34} \right\} n^{-1/5} \]
其中，\( \sigma \) 是样本标准差，\( IQR \) 是四分位距，\( n \) 是样本大小。

交叉验证方法包括留一法（leave-one-out cross-validation，简称LOOCV）和最小化交叉验证均方误差（cross-validation mean square error，简称CV-MSE）等。这些方法通过优化准则函数，可以更客观地选择带宽。

## 2.4 核密度估计的实践技巧

### 2.4.1 使用Python进行核密度估计

Python通过`scipy`和`numpy`库提供了核密度估计的功能。这里展示一个简单的使用例子：

import numpy as np
from scipy.stats import gaussian_kde

# 假设有一些样本数据
data = np.random.randn(100)

# 创建核密度估计器对象
kde = gaussian_kde(data)

# 计算在一组点上的密度估计值
x = np.linspace(-4, 4, 200)
density_values = kde.evaluate(x)

# 输出结果
print(density_values)

在上述代码中，我们首先生成了一组随机数据，然后使用`gaussian_kde`方法创建了一个高斯核密度估计器，并在一系列点上计算了概率密度估计值。

### 2.4.2 核密度估计的参数调优案例

核密度估计参数调优的案例，可以使用交叉验证的方法选择带宽。以下代码展示了使用`scipy`库中`gaussian_kde`的带宽选择过程：

import numpy as np
from scipy.stats import gaussian_kde
from sklearn.model_selection import GridSearchCV

# 创建样本数据
data = np.random.randn(100)

# 设置带宽候选值
bandwidths = np.logspac