ISO-2859-1抽样计划设计：中文版步骤、技巧及误区揭秘


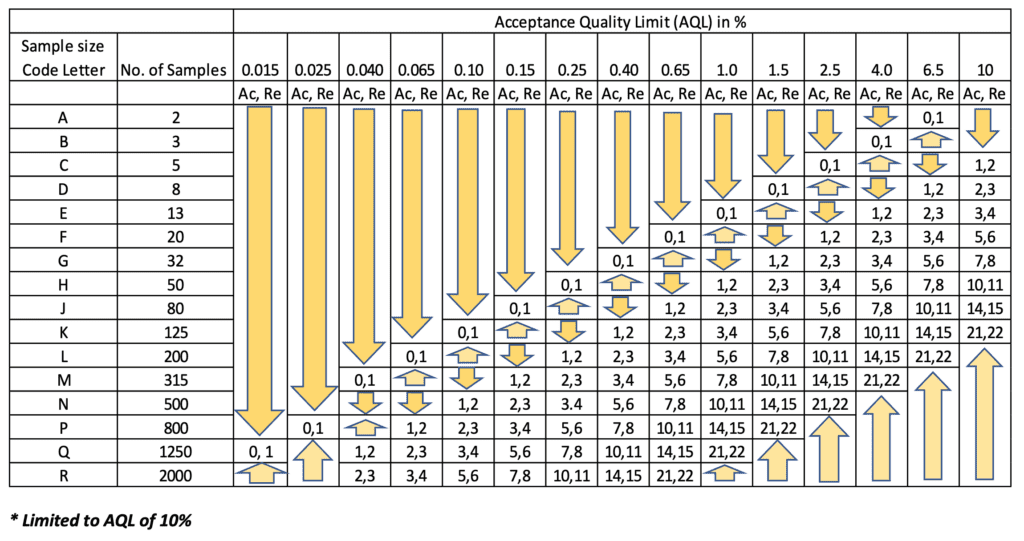
参考资源链接：[ISO2859-1标准解读：属性检验与AQL抽样规则](https://wenku.csdn.net/doc/2v0ix307mq?spm=1055.2635.3001.10343)
# 1. ISO-2859-1抽样计划概述

## ISO-2859-1抽样计划的背景与目的

ISO-2859-1抽样计划是一种国际标准化的抽样技术，广泛应用于工业生产和质量控制中。该抽样标准的核心在于提供一种系统化的抽样方法，以减少产品检验过程中的资源浪费并提供有效的质量控制手段。通过实施ISO-2859-1抽样计划，企业能够以统计学原理为基础，选择合适的样本数量进行检验，从而确保生产过程的稳定性和产品的可靠性。简而言之，ISO-2859-1抽样计划通过提供科学、标准化的抽样框架，帮助企业实现成本效益最大化和质量风险最小化。

# 2. ISO-2859-1抽样计划的理论基础

## 2.1 抽样计划的基本概念

### 2.1.1 抽样计划定义及其重要性

在生产和供应链管理中，质量控制是确保产品和服务符合既定标准的关键环节。ISO-2859-1抽样计划提供了一套科学的方法论，用于在保证质量的同时，最小化样本测试的成本和时间。抽样计划是一种通过分析一部分样本数据来推断总体特性的方法。它的核心在于从大量产品中抽取少量样本进行检查，以此评估整批产品质量。

抽样计划的重要性体现在它能够在成本和时间允许的范围内，以较低的风险来预测和保证产品质量。通过合理的抽样计划，企业能够减少检验工作量，缩短产品上市时间，同时还能发现潜在的质量问题，从而提高客户满意度并增强市场竞争力。

### 2.1.2 抽样计划与质量控制的关系

抽样计划是质量控制不可或缺的一环。它作为质量控制过程中的一个工具，帮助组织量化产品质量水平，并为持续改进提供数据支持。通过抽样计划，可以对产品进行分类和评级，进而进行有效的过程控制。

在与质量控制的关系中，抽样计划有助于确定何时需要采取纠正措施来消除质量问题的根本原因。另外，通过统计分析抽样数据，可以检测到趋势和异常情况，防止可能的缺陷扩散到更广泛的产品批次中。

## 2.2 ISO-2859-1抽样标准的结构与原理

### 2.2.1 ISO-2859-1标准的组成框架

ISO-2859-1标准，也称为“连续抽样标准”，提供了用于自动检验和属性检验的抽样计划。这个标准的组成框架包括了抽样表、抽样方案的描述、抽样程序和决策规则等。标准中的每个抽样表都考虑了不同的批量大小、可接受质量水平(AQL)和抽样大小代码字母。

抽样表是ISO-2859-1标准中的核心部分，它们为不同情况下的抽样决策提供了指南。这些表基于统计学原理，提供了针对特定风险水平和质量要求的样本大小推荐。

### 2.2.2 标准化抽样的理论依据

ISO-2859-1抽样标准的理论依据基于概率抽样和统计假设检验。概率抽样意味着每个样本被选中的概率都是已知的，这为推断总体特性提供了数学上的保证。统计假设检验，则允许根据样本数据对总体参数进行判断。

在标准化抽样中，重点是控制两类错误：第一类错误（α错误）是指错误地拒绝一个良好的批次；第二类错误（β错误）是指错误地接受了一个不良批次。抽样计划旨在最小化这两种错误，同时确保结果的可信度和有效性。

## 2.3 抽样技术与统计学原则

### 2.3.1 抽样技术的分类及其适用场景

抽样技术可以分为简单随机抽样、分层抽样、系统抽样、整群抽样等。每种抽样技术都有其适用的场景和目的。简单随机抽样保证每个样本都有相同的被选中的机会，适用于几乎所有的场景。分层抽样通过将总体分成不同的组或层，然后从每一层中进行随机抽样，适用于总体差异较大的情况。系统抽样是从列表中以固定的间隔进行抽样，适用于样本较为均匀分布的情况。整群抽样则是将总体分成多个群组，然后随机选择几个群组进行全面测试，适用于成本较高或难以访问的情况。

在实施抽样计划时，正确选择抽样技术是至关重要的。根据研究目标、总体的特征和资源的限制，选择合适的抽样技术能够提高抽样的准确性和代表性。

### 2.3.2 统计学在抽样计划设计中的应用

统计学提供了评估抽样计划有效性的工具和方法。在设计抽样计划时，统计学原则能够帮助我们确定样本大小、评估误差范围、计算置信区间，以及选择合适的检验方法。

例如，根据总体大小、预期的方差、希望达到的置信水平等因素，可以使用公式或统计软件来计算出所需的样本大小。这样，当检验结果出来后，我们能够有足够的统计力来确定总体参数是否在可接受的范围内。

接下来，为满足内容要求，我将展示一个代码块以及它的逻辑分析：

# 示例：计算所需的样本大小
import numpy as np
from statsmodels.stats.proportion import proportions_ztest

def calculate_sample_size(estimated_proportion, margin_of_error, confidence_level):
    # 计算Z值，对应于置信水平
    alpha = 1 - confidence_level
    z_value = np.abs(np.array(stats.norm.ppf(alpha/2)))
    # 计算所需的样本大小
    sample_size = (z_value**2 * estimated_proportion * (1 - estimated_proportion)) / margin_of_error**2
    return np.ceil(sample_size).astype(int)

# 假设估计比例为0.5（最大方差），允许误差为5%，置信水平为95%
margin_of_error = 0.05
confidence_level = 0.95
estimated_proportion = 0.5

# 计算所需样本大小
required_sample_size = calculate_sample_size(estimated_proportion, margin_of_error, confidence_level)
print(f"对于比例估计为0.5，误差为{margin_of_error}，置