【泛型算法】：设计通用数据结构与高效算法

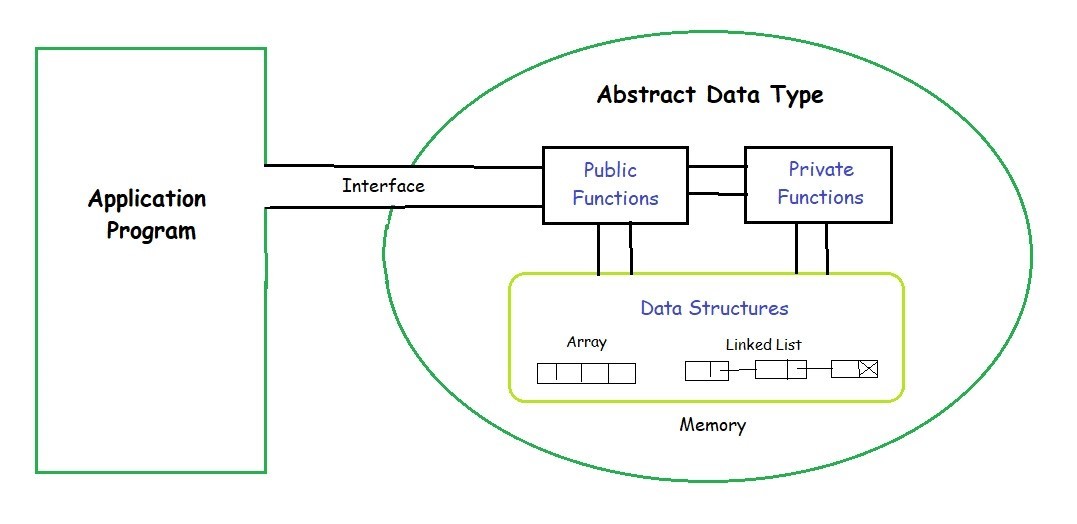
# 1. 泛型算法的基础理论与设计原则

在现代编程实践中，泛型算法是构建高效和可重用软件组件的关键技术之一。本章将从基础理论入手，探讨泛型算法的设计原则和核心概念，为后续章节关于泛型数据结构的设计、实现及其在实际中的应用打下坚实的基础。

## 泛型算法的定义和分类
泛型算法是指那些不依赖于特定数据类型，能够处理多种数据类型的一般性算法。它们通过抽象的方式，将操作定义在一组概念之上，如比较、赋值和复制等，这样算法就不受具体数据类型的限制，增加了代码的复用性。

## 泛型算法的核心特性
泛型算法的主要特性包括类型安全、代码复用和效率。它们能够保持类型安全，因为编译器能在编译时检查类型错误；提高代码复用性，减少重复代码的编写；同时保持效率，因为泛型操作通常不会比针对特定类型的实现慢。

## 泛型算法的设计原则
泛型算法的设计应当遵循简洁、高效和可维护的原则。简洁意味着算法应当尽量减少对操作对象的要求，提高其通用性；高效是指算法在实际使用中应该有良好的时间复杂度和空间复杂度；可维护则是指算法设计应当考虑到未来可能的扩展和维护的便捷性。

# 2. 泛型数据结构的设计与实现

### 2.1 泛型数据结构的基本概念

#### 2.1.1 泛型数据结构的定义和分类

泛型数据结构是指在数据结构的设计与实现中，使用类型参数来允许算法在编译时决定具体数据类型的一种数据结构。这种方式在处理不同的数据类型时可以重用相同的算法和数据结构代码，提高了代码的可复用性和抽象程度。泛型数据结构可以分为线性结构和非线性结构两大类。

线性结构包括：
- 链表：一种通过指针把一系列节点连接起来形成的数据结构。
- 栈：一种后进先出（LIFO）的数据结构，支持压入（push）和弹出（pop）操作。
- 队列：一种先进先出（FIFO）的数据结构，支持入队（enqueue）和出队（dequeue）操作。

非线性结构包括：
- 树：一种分层数据结构，每个节点有零个或多个子节点。
- 图：一种由顶点（节点）的有穷非空集合和顶点之间边的集合构成的结构。

### 2.1.2 泛型数据结构的关键特性分析

泛型数据结构的关键特性包括类型安全、代码复用、灵活性和性能。

- 类型安全：在编译时检查数据类型，可以避免运行时类型错误。
- 代码复用：泛型算法和数据结构可以适用于不同的数据类型，减少了代码量。
- 灵活性：类型参数使得数据结构可以适应更多的数据类型和算法需求。
- 性能：合理设计的泛型数据结构可以接近甚至达到非泛型数据结构的性能。

### 2.2 常见泛型数据结构的设计模式

#### 2.2.1 链表、栈、队列的泛型实现

泛型链表允许在编译时指定元素类型，其节点定义如下：

public class Node<T>
{
    public T Data { get; set; }
    public Node<T> Next { get; set; }

    public Node(T data)
    {
        Data = data;
        Next = null;
    }
}

泛型栈和队列实现类似，主要区别在于它们的操作方法，如 `Push`、`Pop`、`Enqueue`、`Dequeue` 等。

#### 2.2.2 树和图的泛型构建技术

树和图的泛型构建技术需要在节点定义中包含泛型类型，以允许存储不同类型的数据。例如，二叉树的节点定义：

public class TreeNode<T>
{
    public T Value { get; set; }
    public TreeNode<T> Left { get; set; }
    public TreeNode<T> Right { get; set; }

    public TreeNode(T value)
    {
        Value = value;
        Left = null;
        Right = null;
    }
}

图结构的节点可能包含一个邻接节点列表，泛型允许列表中存储任何类型的数据。

#### 2.2.3 映射和集合的泛型操作

映射（Map）和集合（Set）是泛型数据结构中比较复杂的结构，通常由哈希表实现以达到快速的查找性能。例如：

public class HashSet<T>
{
    private Dictionary<T, object> dictionary = new Dictionary<T, object>();

    public void Add(T item)
    {
        if (!dictionary.ContainsKey(item))
        {
            dictionary.Add(item, null);
        }
    }

    // 其他集合操作...
}

### 2.3 泛型数据结构的效率分析

#### 2.3.1 时间复杂度和空间复杂度分析

泛型数据结构的效率分析需要考虑时间复杂度和空间复杂度两个方面。时间复杂度涉及到算法执行的步骤数，空间复杂度涉及到算法执行过程中所占用的内存空间。例如，链表的插入操作通常具有 O(1) 的时间复杂度，但整个结构的空间复杂度是 O(n)，其中 n 是链表的长度。

#### 2.3.2 泛型结构的优化策略

泛型数据结构的优化策略包括：
- 使用更高效的数据存储结构，如平衡二叉搜索树减少查找时间。
- 避免不必要的内存分配，例如，在栈操作中重用节点。
- 对频繁操作进行内联优化，减少函数调用开销。

通过这些策略，可以在保持泛型数据结构灵活性的同时，提高其运行效率。

# 3. 泛型算法的应用实践

在本章节中，我们将探讨泛型算法在实际编程中的应用，包括排序与搜索、数据处理、以及在特定领域中的应用。泛型算法的核心优势在于其能够在多种数据类型上进行高效的通用操作，而这在今天的多样化的软件开发环境中尤其重要。我们将深入探讨如何在具体场景中利用泛型算法来解决实际问题，以及它们所展现的灵活性和效率。

## 3.1 泛型排序与搜索算法

### 3.1.1 泛型快速排序和归并排序

快速排序和归并排序是两种最常用的排序算法，而泛型算法的出现使得它们可以应用于任意类型的集合。泛型快速排序和归并排序的关键在于将比较和交换操作泛化，从而支持不同数据类型的集合排序。

在设计泛型排序算法时，可以采用C++中的模板技术或者Java中的泛型接口。以下是一个泛型快速排序的伪代码示例：

template <typename T>
void quickSort(T arr[], int low, int high) {
    if (low < high) {
        int pivotIndex = partition(arr, low, high);
        quickSort(arr, low, pivotIndex - 1);
        quickSort(arr, pivotIndex + 1, high);
    }
}

template <typename T>
int partition(T arr[], int low, int high) {
    T pivot = arr[high];
    int i = low - 1;
    for (int j = low; j < high; j++) {
        if (arr[j] < pivot) {
            i++;
            std::swap(arr[i], arr[j]);
        }
    }
    std::swap(arr[i + 1], arr[high]);
    return (i + 1);
}

在这个示例中，`quickSort` 函数和 `partition` 函数都是泛型的，可以用于排序任何支持 `<` 操作符的数据类型。泛型归并排序算法的实现原理类似，但主要的区别在于其通过归并两个已排序的子数组来排序整个数组。

### 3.1.2 泛型二分搜索和散列查找

泛型算法不仅在排序算法中占有一席之地，在查找算法中也十分有用。泛型二分搜索是一种有效的查找技术，适用于有序的泛型数组。而泛型散列查找则利用散列表来实现快速查找。

泛型二分搜索算法要求数据结构是有序的，如下示例所示：

template <typename T>
int binarySearch(const T arr[], int l, int r, const T& x) {
    while (l <= r) {
        int m = l + (r - l) / 2;

        if (arr[m] == x)
            return m;

        if (arr[m] < x)
            l = m + 1;
        else
            r = m - 1;
    }

    return -1;
}

此示例中的 `binarySearch` 函数对任何有序集合进行泛型操作，它查找元素 `x` 的位置，如果找到则返回位置索引，否则返回 `-1`。

## 3.2 泛型数据处理技术

### 3.2.1 泛型数据过滤和映射

泛型数据处理技术包括数据过滤和映射等操作。数据过滤是指根据特定条件选择数据集中的元素，而映射则是将数据集中的每个元素转换为另一种形式。

例如，在C++中，我们可以使用STL中的 `std::remove_if` 和 `std::transform` 算法。假设我们有以下的泛型