【算法实战高手】：Labuladong动态规划应用，解决实际问题的不二法门


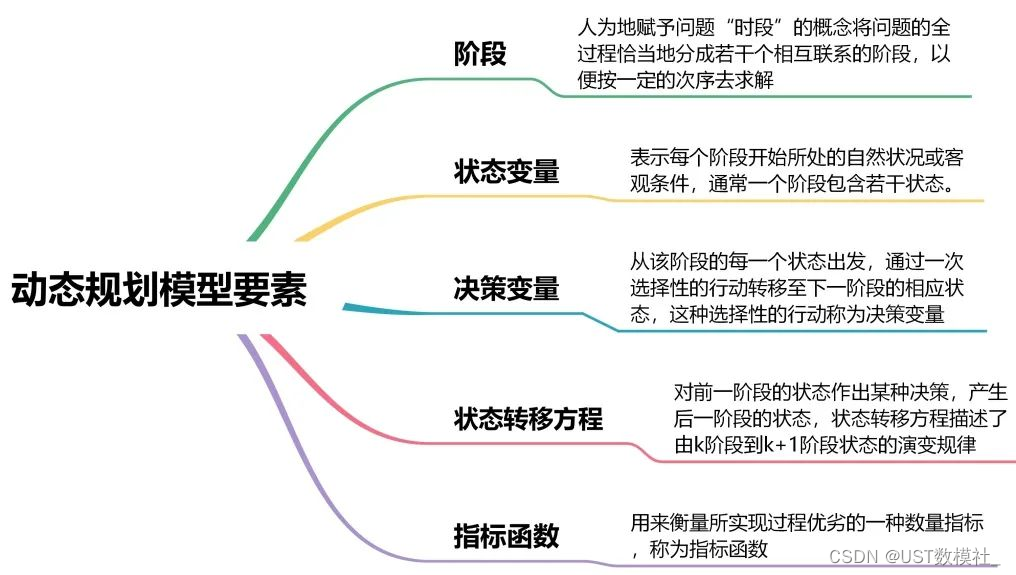
# 摘要
动态规划作为一种解决优化问题的算法策略，在理论和实践层面都具有重要的地位。本文从理论基础讲起，逐步深入解析动态规划的核心概念，包括状态定义、状态转移方程、初始条件和边界情况的处理，以及优化技巧。随后，文章对动态规划问题进行分类讨论，并提供背包问题、序列问题和区间问题的解法实例。实战演练章节通过分析LeetCode题目和面试准备策略，加深对动态规划应用的理解。最后，本文探讨了动态规划在经济学和计算机科学中的实际案例，以及算法进阶和未来发展的方向。

# 关键字
动态规划；状态转移方程；优化技巧；背包问题；序列问题；算法面试；并行化计算

参考资源链接：[labuladong算法秘籍：数据结构与刷题攻略](https://wenku.csdn.net/doc/5ss8mev03x?spm=1055.2635.3001.10343)
# 1. 动态规划理论基础

## 1.1 动态规划简介
动态规划（Dynamic Programming，DP）是解决多阶段决策过程优化问题的一种方法。它将复杂问题拆分成更小的子问题，并存储这些子问题的解，避免重复计算。动态规划特别适用于具有重叠子问题和最优子结构特性的问题。

## 1.2 动态规划的适用条件
为了有效地应用动态规划，问题必须满足两个重要条件：
- 最优子结构：问题的最优解包含其子问题的最优解。
- 重叠子问题：在解决问题的过程中，相同的子问题会被多次求解。

## 1.3 动态规划的求解步骤
通常，动态规划求解问题的步骤可以分为以下几个阶段：
1. 定义状态：确定决策变量和状态变量。
2. 状态转移方程：找出状态之间的递推关系。
3. 初始条件和边界情况：为递推过程设定起点。
4. 计算顺序：确定计算状态的顺序。
5. 结果提取：从计算结果中提取问题的解。

动态规划是计算复杂性理论中一个重要的算法设计技巧，广泛应用于各种优化问题，如资源分配、路径搜索等领域。掌握动态规划的关键在于熟练掌握以上各个步骤，以及对不同问题进行适当的变通和抽象。接下来的章节将对动态规划的核心概念进行更详细的解释。

# 2. 动态规划核心概念详解

### 2.1 状态和状态转移方程

动态规划的核心在于定义问题的“状态”和从一个状态转移到另一个状态的规律，即“状态转移方程”。理解并正确表达这两个概念是解决动态规划问题的关键步骤。

#### 2.1.1 定义状态

在动态规划问题中，状态通常是指解决问题过程中某一阶段的结果。一个状态通常由一个或多个参数构成，这些参数的变化范围定义了状态空间的大小。例如，在背包问题中，状态可以是当前背包中物品的总重量和总价值。

以0-1背包问题为例，定义一个状态s[i][v]表示考虑前i个物品，当前背包容量为v时能够达到的最大价值。这样定义的状态s能够准确描述问题的动态变化。

def dp(N, W, weights, values):
    # 初始化状态数组，维度为(N+1) * (W+1)，初始值为0
    dp = [[0] * (W + 1) for _ in range(N + 1)]
    # 遍历所有物品
    for i in range(1, N + 1):
        # 遍历所有可能的重量
        for v in range(W + 1):
            # 如果当前物品的重量小于等于背包容量
            if weights[i-1] <= v:
                # 状态转移方程，取最大值
                dp[i][v] = max(dp[i-1][v], dp[i-1][v-weights[i-1]] + values[i-1])
            else:
                # 如果当前物品重量大于背包容量，则不装入背包
                dp[i][v] = dp[i-1][v]
    return dp[N][W]

这段代码初始化了一个二维数组dp，用于保存每一个状态的最优解，N是物品的个数，W是背包的最大容量。通过遍历物品和重量，我们可以填充这个数组，最终dp[N][W]就是问题的解。

#### 2.1.2 设计状态转移方程

状态转移方程是动态规划的灵魂，它描述了从一个状态如何转变到另一个状态。在定义好状态之后，需要找到状态之间的转换逻辑。

在0-1背包问题中，状态转移方程可以表示为：

dp[i][v] = max(dp[i-1][v], dp[i-1][v-weights[i-1]] + values[i-1])

这个方程表明，对于第i个物品，有两种选择：不放入背包和放入背包。如果不放入背包，那么最大价值就是前i-1个物品在容量为v时的最大价值；如果放入背包，最大价值则是前i-1个物品在容量为v-weights[i-1]的最大价值加上当前物品的价值。

这个方程完整地描述了动态规划问题的状态转移过程，是解题过程中的关键。

### 2.2 初始条件和边界情况

在构建动态规划算法时，初始条件和边界情况的确定同样重要。它们是状态转移方程能够正确运行的基础。

#### 2.2.1 确定初始条件

初始条件通常指的是状态数组的边界值，也就是状态空间中最小的一个单元。在动态规划中，初始条件往往是解题的基础，它将为后续的状态转移提供依据。

例如，在0-1背包问题中，初始条件可以设置为dp[i][0] = 0（对于所有的i），表示背包容量为0时，不管物品数量如何，最大价值都是0。另一个初始条件是dp[0][v] = 0（对于所有的v），表示没有物品时，背包容量无论大小，最大价值都是0。

#### 2.2.2 处理边界情况

在实际问题中，除了初始条件之外，还需要特别注意处理那些可能会导致状态转移方程无法直接应用的边界情况。例如，如果物品的重量超过了背包的容量，那么这个物品就不应该被加入到背包中。

在背包问题中，当考虑一个物品的重量超过当前背包容量时，状态转移方程应该直接取不装入该物品的情况，即dp[i][v] = dp[i-1][v]。在编写代码时，可以通过if语句来确保不会出现负数索引或非法的状态转移。

def knapsack(weights, values, W):
    N = len(weights)
    dp = [0] * (W + 1)

    for i in range(N):
        for v in range(W, weights[i] - 1, -1):
            # 状态转移方程，考虑边界情况
            dp[v] = max(dp[v], dp[v - weights[i]] + values[i])

    return dp[W]

上述代码中，通过从后往前遍历背包容量，我们有效避免了在更新dp[v]时使用到尚未计算的dp[v]值，这是一种处理边界情况的常见技巧。

### 2.3 优化技巧与方法

动态规划算法的优化是提高效率的关键，通过优化可以减少不必要的计算，从而使得算法在处理大规模数据时仍然能够保持较高的效率。

#### 2.3.1 状态压缩技术

状态压缩是减少动态规划空间复杂度的常用技术。在很多动态规划问题中，状态的下一个状态只依赖于少量的前驱状态，这时可以利用位运算来压缩状态空间。

例如，如果状态只依赖于前一个状态，那么可以使用一个整数变量来存储状态，通过位运算来模拟状态的转移。

def count_bits(x):
    # 计算整数x的二进制表示中1的个数
    count = 0
    while x:
        count += x & 1
        x >>= 1
    return count

def state_compression_dp(N, W, weights, values):
    # 初始化一个一维数组，大小为W+1
    dp = [0] * (W + 1)

    for i in range(N):
        # 从大到小遍历容量
        for v in range(W, weights[i] - 1, -1):
            # 利用位运算更新状态
            dp[v] = max(dp[v], dp[v - weights[i]] + values[i])

    return dp[W]

在这个例子中，我们只用了一个一维数组dp来存储状态，通过位运算来处理状态转移。

#### 2.3.2 时间和空间复杂度优化

动态规划算法的时间和空间复杂度优化是算法优化中不可忽视的部分。通过减少不必要的计算以及利用额外的空间来存储中间结果，可以大幅提升算法性能。

以背包问题为例，如果我们使用一个二维数组来存储状态，那么空间复杂度为O(NW)，但通过状态压缩，我们可以将空间复杂度降低至O(W)。

对于时间复杂度的优化，可以考虑使用更高效的数据结构，如有序集合或者平衡二叉搜索树等，来存储中间结果，并减少查找时间。在一些动态规划问题中，可以应用滚动数组的技术，通过循环覆盖的方法减少空间的使用。

def time_and_space_optimization_dp(N, W, weights, values):
    # 初始化两个一维数组，用于滚动覆盖
    prev_dp = [0] * (W + 1)
    curr_dp = [0] * (W + 1)

    for i in range(1, N + 1):
        for v in range(W, weights[i-1] - 1, -1):
            # 使用滚动数组更新状态
            curr_dp[v] = max(prev_dp[v], prev_dp[v - weights[i-1]] + values[i-1])
        # 滚动数组更新，将当前数组内容复制到前一个数组
        for j in range(W + 1):
            prev_dp[j] = curr_d