单片机控制系统PID控制秘籍：理论与实践

# 1. PID控制理论基础**

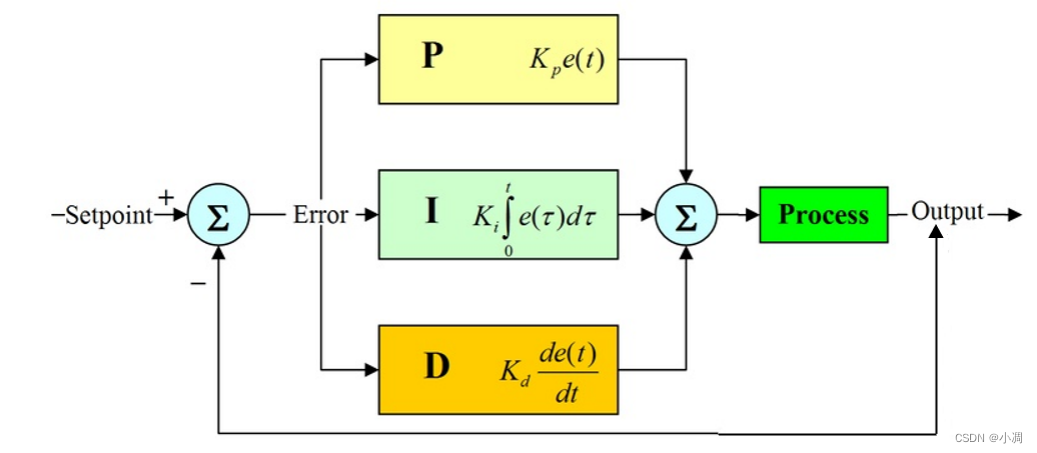
PID控制是一种闭环控制算法，它通过测量系统输出与期望输出之间的误差，并根据误差的大小和变化率来调整控制输出，从而达到控制目标。PID控制算法的原理和结构如下：

- **比例项（P）：**与误差成正比，用于快速响应误差变化。
- **积分项（I）：**与误差的积分成正比，用于消除稳态误差。
- **微分项（D）：**与误差的变化率成正比，用于预测误差变化并提前做出响应。

# 2. PID控制算法实现

### 2.1 PID算法的原理和结构

PID算法（比例-积分-微分算法）是一种经典的反馈控制算法，广泛应用于单片机控制系统中。其原理是根据被控对象的偏差（误差）信号，通过比例（P）、积分（I）和微分（D）三个环节进行综合计算，从而输出控制信号，使被控对象达到期望状态。

PID算法的结构如下图所示：

graph LR
    subgraph PID算法
        A[误差] --> B[比例环节] --> C[积分环节] --> D[微分环节] --> E[控制信号]
    end

**比例环节（P）**：根据误差信号的大小，按比例输出控制信号。比例系数Kp越大，控制信号越大，响应越快，但容易产生振荡。

**积分环节（I）**：根据误差信号的积分值，输出控制信号。积分时间Ti越大，积分作用越强，可以消除稳态误差，但响应速度较慢。

**微分环节（D）**：根据误差信号的变化率，输出控制信号。微分时间Td越大，微分作用越强，可以提高控制系统的稳定性，但容易产生噪声。

### 2.2 PID算法的调参方法

PID算法的调参至关重要，直接影响控制系统的性能。常用的调参方法有：

#### 2.2.1 Ziegler-Nichols方法

该方法基于被控对象的阶跃响应曲线，通过测量上升时间（Tu）和峰值时间（Tp），根据下表确定PID参数：

| 控制类型 | Kp | Ti | Td |
|---|---|---|---|
| P | 0.5Tu | - | - |
| PI | 0.45Tu | 0.85Tu | - |
| PID | 0.6Tu | 0.5Tu | 0.125Tu |

#### 2.2.2 Cohen-Coon方法

该方法基于被控对象的传递函数，通过测量时延（L）和时间常数（T），根据下表确定PID参数：

| 控制类型 | Kp | Ti | Td |
|---|---|---|---|
| P | 1.2 / L | - | - |
| PI | 2 / L | 0.5L | - |
| PID | 3.2 / L | 0.4L | 0.8L |

### 2.3 PID算法的仿真和验证

在实际应用之前，通常需要对PID算法进行仿真和验证，以确保其性能满足要求。可以使用MATLAB、Simulink等仿真工具，构建PID控制系统的模型，并输入各种输入信号进行仿真。通过观察输出响应曲线，可以评估PID算法的稳定性、响应速度和抗干扰能力等性能指标。

# 3. 单片机PID控制实践**

### 3.1 单片机PID控制系统硬件设计

单片机PID控制系统硬件主要包括单片机、传感器、执行器、电源等。

**单片机：**选择具有足够处理能力和存储空间的单片机，如STM32系列、MSP430系列等。

**传感器：**根据被控对象的类型选择合适的传感器，如温度传感器、压力传感器、位置传感器等。

**执行器：**根据被控对象的类型选择合适的执行器，如电机、电磁阀、继电器等。

**电源：**为系统提供稳定的电源，通常使用稳压电源或电池。

**硬件设计步骤：**

1. 根据被控对象和控制要求确定硬件配置。
2. 选择合适的单片机、传感器、执行器和电源。
3. 设计电路原理图和PCB板。
4. 焊接和调试硬件。

### 3.2 单片机PID控制软件实现

#### 3.2.1 PID算法的移植

将PID算法移植到单片机中，需要考虑单片机的硬件资源和实时性要求。

**移植步骤：**

1. 将PID算法的数学公式转换为单片机可执行的代码。
2. 根据单片机的寄存器和中断机制优化代码效率。
3. 编写PID算法的初始化函数、计算函数和输出函数。

#### 3.2.2 控制策略的优化

除了PID算法本身，还需要优化控制策略以提高系统的性能。

**优化策略：**

**采样时间：**根据被控对象的动态特性选择合适的采样时间。采样时间过长会导致控制延迟，过短会导致计算量增加。

**积分项：**积分项可以消除稳态误差，但过大的积分增益会导致系统不稳定。

**微分项：**微分项可以提高系统的响应速度，但过大的微分增益会导致系统振荡。

**抗积分饱和：**当积分项累积过大时，可能会导致系统饱和，需要采取抗积分饱和措施。

**代码示例：**

// PID算法计算函数
void PID_Calc(float setpoint, float feedback) {
  // 计算误差
  float error = setpoint - feedback;

  // 计算积分
  integral += error * dt;

  // 计算微分
  derivative = (error - prev_error) / dt;

  // 计算输出
  output = kp * error + ki * integral + kd * derivative;

  // 抗积分饱和
  if (output >