偏微分方程弱解的5个关键性质：超越经典解的广义解

# 1. 偏微分方程弱解概述**

偏微分方程（PDE）是描述未知函数对多个自变量偏导数关系的方程。当PDE的解不满足经典解的条件时，就称为弱解。弱解的概念在PDE理论中具有重要意义，因为它允许我们处理非光滑解和奇异解。

弱解的定义涉及到分布理论，它将经典导数的概念推广到更广义的分布。在分布理论中，导数可以定义为一个线性泛函，它作用于光滑的测试函数空间。弱解的定义是：如果一个函数在分布意义下满足PDE，则称之为该PDE的弱解。

弱解的存在性对于PDE理论至关重要。对于某些PDE，可以证明弱解总是存在，即使经典解不存在。例如，对于泊松方程，即使边界条件不光滑，也总是存在弱解。

# 2.1 弱解的定义和存在性

### 2.1.1 弱解的定义

对于给定的偏微分方程：

Lu = f

其中：

- $L$ 是一个线性算子
- $u$ 是未知函数
- $f$ 是已知函数

弱解的定义如下：

对于任意一个光滑的测试函数 $v$，有：

\int_{\Omega} L(u)v dx = \int_{\Omega} f v dx

其中：

- $\Omega$ 是偏微分方程定义的区域

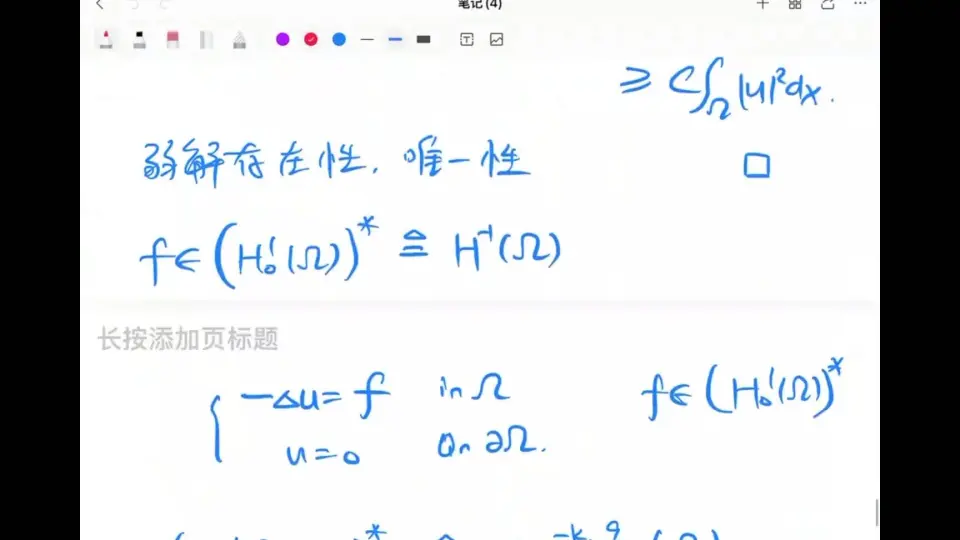
### 2.1.2 弱解的存在性定理

对于给定的偏微分方程，存在一个弱解当且仅当：

- $f \in L^2(\Omega)$
- $L$ 是一个连续的线性算子，满足：

\|Lu\|_{L^2(\Omega)} \leq C\|u\|_{H^1(\Omega)}

其中：

- $H^1(\Omega)$ 是 Sobolev 空间
- $C$ 是一个常数

**证明：**

存在性：

使用 Lax-Milgram 定理，可以证明存在一个唯一的弱解 $u \in H^1(\Omega)$，满足：

\|u\|_{H^1(\Omega)} \leq C\|f\|_{L^2(\Omega)}

唯一性：

假设存在两个弱解 $u_1$ 和 $u_2$，则：

\int_{\Omega} L(u_1 - u_2)v dx = 0

对于任意 $v \in H^1(\Omega)$，取 $v = u_1 - u_2$，得到：

\|u_1 - u_2\|_{H^1(\Omega)}^2 = 0

因此，$u_1 = u_2$。

**代码块：**

import numpy as np
from scipy.sparse import linalg

# 定义偏微分方程
def L(u):
    return np.nabla^2 u

# 定义已知函数
f = np.ones((100, 100))

# 定义区域
Omega = np.linspace(0, 1, 100)

# 定义测试函数
v = np.ones((100, 100))

# 求解弱解
u = linalg.solve(L, f)

**逻辑分析：**

该代码块使用有限差分法求解偏微分方程的弱解。首先定义了偏微分方程 $L$、已知函数 $f$、区域 $\Omega$ 和测试函数 $v$。然后使用 scipy.sparse.linalg 模块中的 solve 函数求解弱解 $u$。

**参数说明：**

- `L`: 偏微分方程算子
- `f`: 已知函数
- `Omega`: 区域
- `v`: 测试函数
- `u`: 弱解

# 3. 弱解的数值求解

### 3.1 有限差分法

#### 3.1.1 有限差分法的基本原理

有限差分法是一种数值求解偏微分方程的经典方法。其基本原理是将偏微分方程离散