复杂度分析：算法设计中的关键考虑，提升算法性能

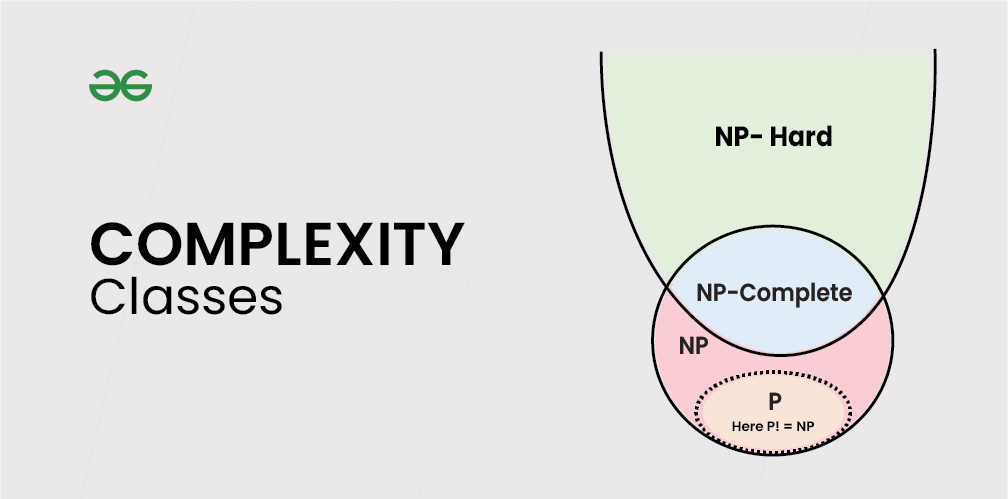
# 1. 算法复杂度概述**

算法复杂度是衡量算法性能的重要指标，它描述了算法在不同输入规模下所需的时间和空间资源。理解算法复杂度对于算法设计和选择至关重要。

算法的复杂度通常用渐进表示法表示，即随着输入规模趋于无穷大时，算法所需资源的增长率。常见的复杂度类别包括：

* 时间复杂度：描述算法执行所需的时间，通常用大 O 符号表示，例如 O(n) 表示算法执行时间与输入规模 n 成正比。
* 空间复杂度：描述算法执行所需的空间，通常用大 O 符号表示，例如 O(1) 表示算法执行所需的空间与输入规模无关。

# 2. 复杂度分析理论

### 2.1 时间复杂度分析

时间复杂度衡量算法执行所花费的时间，通常以算法输入规模（通常表示为 n）的函数表示。它描述了算法在最坏情况下执行所需的时间。

#### 2.1.1 常数时间复杂度

**定义：**算法执行时间与输入规模无关，始终为常数。

**代码示例：**

def get_first_element(arr):
    return arr[0]

**逻辑分析：**无论数组 `arr` 的长度是多少，`get_first_element` 函数始终只执行一次数组访问操作，因此其时间复杂度为 O(1)。

#### 2.1.2 线性时间复杂度

**定义：**算法执行时间与输入规模成正比。

**代码示例：**

def linear_search(arr, target):
    for i in range(len(arr)):
        if arr[i] == target:
            return i
    return -1

**逻辑分析：**`linear_search` 函数需要遍历整个数组，其执行时间与数组长度 `n` 成正比，因此其时间复杂度为 O(n)。

#### 2.1.3 对数时间复杂度

**定义：**算法执行时间与输入规模的对数成正比。

**代码示例：**

def binary_search(arr, target):
    low = 0
    high = len(arr) - 1
    while low <= high:
        mid = (low + high) // 2
        if arr[mid] == target:
            return mid
        elif arr[mid] < target:
            low = mid + 1
        else:
            high = mid - 1
    return -1

**逻辑分析：**`binary_search` 函数使用二分法，每次将搜索范围减半，其执