微服务架构设计与实现：从概念到实战应用

# 1. 微服务架构概述

微服务架构是一种软件设计风格，将应用程序分解为一组松散耦合、独立部署的微服务。每个微服务负责特定功能，并通过轻量级通信机制相互通信。

微服务架构提供了许多好处，包括：

- **可扩展性：** 微服务可以独立扩展，以满足不断变化的负载需求。
- **灵活性：** 微服务可以轻松地添加、删除或替换，以适应新的业务需求。
- **可维护性：** 微服务易于维护和更新，因为它们是独立部署的，并且具有明确定义的接口。

# 2. 微服务架构设计**

微服务架构是一种软件架构风格，它将应用程序分解为一组松散耦合、独立部署的微服务。与传统单体应用程序相比，微服务架构具有许多优点，包括：

- **可扩展性：**微服务可以独立扩展，而无需影响其他服务。
- **可维护性：**微服务易于维护，因为它们是独立的单元。
- **灵活性：**微服务可以根据需要轻松添加或删除，从而使应用程序更具灵活性。

## 2.1 架构原则和最佳实践

### 2.1.1 松散耦合和高内聚

松散耦合是指微服务之间依赖关系较弱。这使得微服务可以独立开发和部署，而不会影响其他服务。高内聚是指微服务具有明确定义的职责，并且只关注特定功能。这有助于提高应用程序的可维护性和可扩展性。

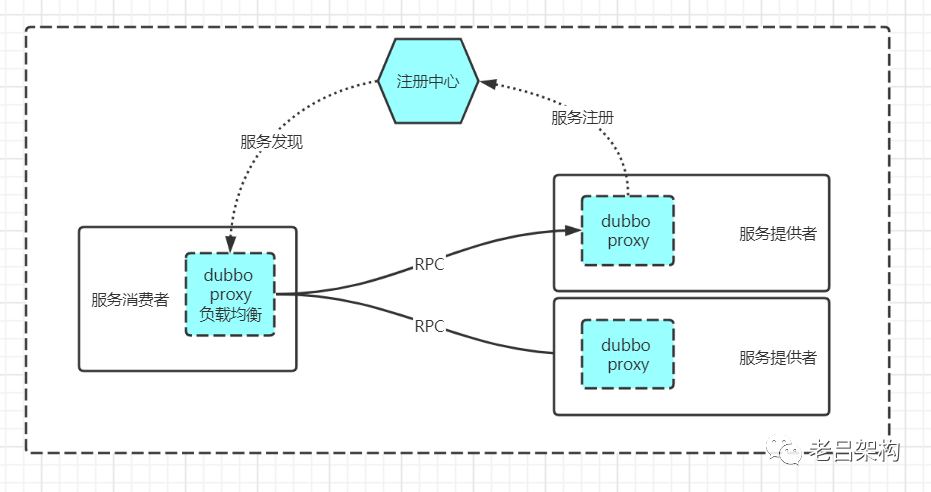
### 2.1.2 服务发现和负载均衡

服务发现是微服务架构中的一项关键机制，它允许微服务相互发现并进行通信。负载均衡是一种技术，它将请求分布到多个微服务实例，以提高应用程序的可用性和性能。

## 2.2 服务设计模式

### 2.2.1 RESTful API设计

RESTful API是一种基于HTTP协议的API设计风格。RESTful API使用一组标准化的HTTP动词（如GET、POST、PUT、DELETE）来执行不同的操作。RESTful API易于使用和理解，并且可以与各种客户端语言和框架集成。

### 2.2.2 事件驱动的架构

事件驱动的架构是一种软件架构风格，它使用事件来触发微服务之间的通信。事件是描述应用程序中发生的事情的消息。事件驱动的架构可以提高应用程序的松散耦合和可扩展性。

## 2.3 通信机制

### 2.3.1 HTTP/HTTPS

HTTP/HTTPS是用于在Web上发送和接收数据的标准协议。HTTP/HTTPS是微服务之间通信最常用的协议。

### 2.3.2 消息队列

消息队列是一种中间件，它允许微服务异步通信。消息队列存储消息，以便微服务可以在需要时检索它们。消息队列可以提高应用程序的可靠性和可扩展性。

**代码示例：**

# 使用 RESTful API 进行通信
import requests

# 发送 GET 请求
response = requests.get("http://example.com/api/v1/users")

# 解析 JSON 响应
users = response.json()

# 使用消息队列进行通信
import pika

# 连接到消息队列
connection = pika.BlockingConnection(pika.ConnectionParameters("localhost"))

# 创建信道
channel = connection.channel()

# 声明队列
channel.queue_declare(queue="my-queue")

# 发布消息
channel.basic_publish(exchange="", routing_key="my-queue", body="Hello, world!")

# 消费消息
def callback(ch, method, properties, body):
    print("Received message: {}".format(body))

channel.basic_consume(callback, queue="my-queue", no_ack=True)

# 开始消费消息
channel.start_consuming()

**逻辑分析：**

* RESTful API示例使用requests库发送HTTP GET请求并解析JSON响应。
* 消息队列示例使用pika库连接到消息队列，声明队列，发布消息并消费消息。

**参数说明：**

* **requests.get()**：发送HTTP GET请求。
* **response.json()**：解析JSON响应。
* **pika.BlockingConnection()**：连接到消息队列。
* **channel.queue_declare()**：声明队列。
* **channel.basic_publish()**：发布