【PID控制原理与应用】：揭秘PID算法如何在工业自动化中成为关键


# 摘要
PID（比例-积分-微分）控制是工业自动化中广泛使用的控制策略，它通过调整控制系统的比例、积分和微分参数以达到期望的控制效果。本文首先概述了PID控制原理，然后深入解析PID控制器的理论基础和组成，包括P、I、D三种控制方式的作用与影响，以及参数调整方法。文章进一步探讨了PID控制算法的数学模型及其在计算机中的实现。在应用案例章节，通过温度、流量和位置控制系统的需求分析和设计实现，展示了PID控制在工业自动化中的实际应用。最后，本文介绍了PID控制的高级应用与优化，包括多变量控制、非线性控制，以及利用先进优化技术如遗传算法、神经网络和预测控制对PID进行优化的研究进展。

# 关键字
PID控制；比例控制；积分控制；微分控制；自动化；优化技术

参考资源链接：[TwinCAT PLC Control PID库详细指南：功能块与应用实例](https://wenku.csdn.net/doc/7ez3qkgfrn?spm=1055.2635.3001.10343)
# 1. PID控制原理概述

PID控制是一种常见的反馈控制算法，广泛应用于工业自动化领域。它通过比例（P）、积分（I）、微分（D）三个基本控制动作的组合，实现对被控制对象的精确控制。PID控制的原理可以简单概述为：根据期望值和实际测量值的差异（即误差），计算出一个控制量，该控制量通过调整被控制对象的输入，以减少误差，从而达到控制目标。本章将初步介绍PID控制的基本概念，为后续深入理解和应用PID控制打下基础。

# 2. 深入解析PID控制器的组成

## 2.1 PID控制器的理论基础
### 2.1.1 比例（P）控制的作用和影响

比例控制是PID控制器中最为直观的部分，其作用是对系统的偏差进行量化，并产生相应的控制作用。在比例控制中，控制器输出与系统偏差成正比，即偏差越大，控制器产生的作用也越强。在数学表达上，比例控制可以表示为：

\[ u(t) = K_p \cdot e(t) \]

其中，\( u(t) \)是控制器在时间\( t \)的输出，\( e(t) \)是当前时刻的系统偏差，\( K_p \)是比例增益。

比例控制对系统响应有快速反应的效果，但往往不能消除稳态误差，而且过高的比例增益可能导致系统振荡。为了减少这些问题，积分和微分控制被引入PID控制器中。

### 2.1.2 积分（I）控制的作用和影响

积分控制的作用是消除系统长期存在的稳态误差。它通过累积偏差的值（即积分）来产生控制器的输出。在数学上，积分控制可以表示为：

\[ u(t) = K_i \cdot \int_{0}^{t} e(\tau) d\tau \]

在这里，\( K_i \)是积分增益，\( e(\tau) \)是时间从\( 0 \)到\( t \)的偏差值的积分。

积分控制使系统能够消除长期稳态误差，但是它可能增加系统的响应时间并引起较大的超调。因此，与比例控制相结合使用是常见的做法。

### 2.1.3 微分（D）控制的作用和影响

微分控制通过预测系统的未来行为来减少或防止超调。它根据偏差的变化率产生控制器的输出，数学上可以表示为：

\[ u(t) = K_d \cdot \frac{de(t)}{dt} \]

在上式中，\( K_d \)是微分增益，\( \frac{de(t)}{dt} \)是偏差变化率。

微分控制提供了一种机制，使控制器能够提前对偏差的变化做出反应，减小超调和振荡。但是，它对噪声非常敏感，因此通常与比例和积分控制结合使用。

## 2.2 PID控制器的参数调整

### 2.2.1 参数调整方法概述

PID控制器的参数调整是一个关键步骤，它决定了控制器性能的好坏。参数调整方法大致可以分为三类：手动调整、基于规则的方法和基于优化的方法。

手动调整方法依赖于工程师的经验和直觉。基于规则的方法，如Ziegler-Nichols方法，提供了一套调整规则来获取初步参数，然后基于系统响应进行微调。基于优化的方法，如使用遗传算法或模拟退火算法，可以自动找到最佳的PID参数组合，以达到最优的控制效果。

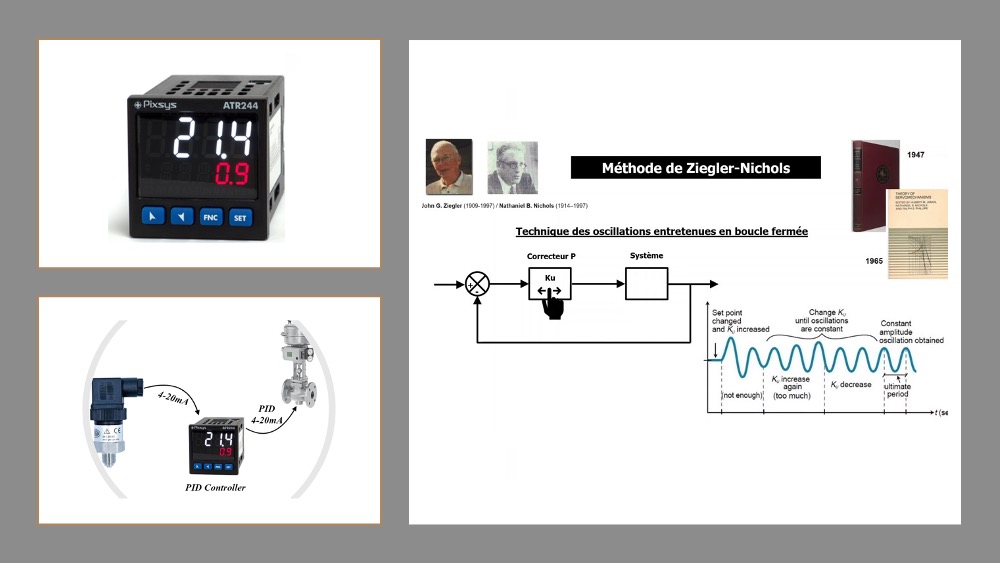
### 2.2.2 Ziegler-Nichols方法详解

Ziegler-Nichols方法是自动PID控制器参数调整中最著名的方法之一。它通过以下步骤进行参数调整：

1. 设置\( K_p \)和\( K_i \)为零，\( K_d \)保持非零值。
2. 逐步增加\( K_p \)，直到系统振荡，记录此时的\( K_p \)值（即临界增益\( K_{cr} \)）。
3. 测量振荡周期\( T_{cr} \)。
4. 根据振荡条件下的临界参数，应用Ziegler-Nichols提供的公式来设置PID参数：

\[ K_p = 0.6 \cdot K_{cr} \]
\[ K_i = 1.2 \cdot K_p / T_{cr} \]
\[ K_d = 0.075 \cdot K_p \cdot T_{cr} \]

### 2.2.3 Cohen-Coon方法详解

Cohen-Coon方法是一种基于过程模型的参数调整方法。它首先需要获取系统的脉冲响应，并基于此建立一个简化的过程模型。然后，根据模型的特性参数来计算PID控制器的参数。这种方法比Ziegler-Nichols更为复杂和精确，但在获取系统脉冲响应数据方面可能存在困难。

## 2.3 PID控制算法的实现

### 2.3.1 PID控制算法的数学模型

PID控制算法的数学模型通常表示为一个线性微分方程，它描述了控制器的输出\( u(t) \)与系统偏差\( e(t) \)之间的关系：

\[ u(t) = K_p \cdot e(t) + K_i \cdot \int_{0}^{t} e(\tau) d\tau + K_d \cdot \frac{de(t)}{dt} \]

该模型涉及到比例、积分和微分三个部分，需要通过选择合适的\( K_p \)、\( K_i \)和\( K_d \)来优化控制效果。

### 2.3.2 PID控制算法的计算机实现

在计算机实现PID控制器时，通常使用离散时间模型来替代连续时间模型。这是因为计算机处理的都是离散的数据。离散时间的PID控制器公式表示为：

\[ u(k) = K_p \cdot e(k) + K_i \cdot T \cdot \sum_{j=0}^{k} e(j) + K_d \cdot \frac{e(k) - e(k-1)}{T} \]

其中，\( u(k) \)是在第\( k \)个采样时刻的控制器输出，\( T \)是采样时间间隔，\( e(k) \)是第\( k \)个采样时刻的偏差。

代码块通常用于展示PID算法在编程语言中的具体实现方式。

// C语言中简单的PID控制算法实现示例
double Kp = 1.0, Ki = 0.1, Kd = 0.05;
double previous_error = 0.0;
double integral = 0.0;
double dt = 0.1; // 假设的采样时间间隔

void update_pid(double setpoint, double measured_value) {
    double error = setpoint - measured_value;
    integral += error * dt;
    double derivative = (error - previous_error) / dt;
    double output = Kp*error + Ki*integral + Kd*derivative;
    // 将output应用到被控对象
    // ...
    previous_error = error;
}

// 使用update_pid函数进行周期性的控制更新

在上述代码中，我们看到一个简单的PID控制器的实现，涉及到比例、积分和微分的计算。通过不断地调用`update_pid`函数并更新控制输出，我们可以实现对一个过程的PID控制。

继续本章节深入的内容，下文将对PID控制在工业自动化中的应用进行详细的案例分析。

# 3. PID控制在工业自动化中的应用案例

在现代工业自动化领域，PID控制器因其结构简单、可靠性高以及易于理解和实现等特点，已经成为了一种标准的控制方式。这一章将介绍PID控制在不同工业应用中的实际案例，深入分析其设计与实现过程，并对特定案例进行详细的探讨。

## 3.1 温度控制系统

### 3.1.1 温度控制的需求分析

在众多工业过程中，温度控制是一个关键的环节。从化学反应的精确控制到食品加工和材料处理，温度必须保持在一定的范围内以确保过程的安全和产品的质量。温度控制系统的需求分析通常需要考虑如下几个因素：

- 稳定性：系统的输出需要维持在一个目标温度值附近，波动幅度要小。
- 响应速度：系统对温度变化的响应需要尽可能快，以减少过冲和振荡。
- 抗干扰能力：温度控制系统需要能够抵抗环境噪声和内部干扰的影响。

### 3.1.2 PID控制器的设计与实现

在设计一个温度控制的PID系统时，通常会遵循以下步骤：

1. 选择合适的传感器来精确测量当前温度。
2. 使用一个微控制器或PLC（可编程逻辑控制器）来实现PID算法。
3. 设定PID控制参数，即比例（P）、积分（I）和微分（D）。
4. 将计算出的控制量转换为相应的驱动信号，驱动加热或冷却设备。

PID控制算法的数学模型在此场景中的表现是通过调整温度来达到和保持目标温度。这涉及到三个环节的运算：比例环节决定当前偏差的响应大小；积分环节累计偏差，消除静态误差；微分环节预测偏差趋势，提前调整控制量以防止过冲。

### 3.1.3 案例分析：某工厂热处理过程的温度控制

在某汽车零件制造厂的热处理过程中，需要对零件进行精确的温度控制，以达到材料的机械性能要求。工厂采用了一个PID控制系统来维持炉内温度的稳定。

系统实现的步骤如下：

- 首先，通过热电偶实时监测炉内温度。
- 数据通过模拟信号转换器进入PLC。
- PLC内部实现PID控制算法，计算出控制量。
- 控制量通过数字输出驱动加热元件，或者开启冷却系统。
- 通过调整PID参数，实现对炉内温度的精确控制。

系统中PID参数的优化是通过不断的试验和调整，依据经验和实际效果进行调整。在生产中，还会有安全检测机制，一旦温度超出预定范围，系统会自动进入安全模式，以保护设备和操作人员的安全。

## 3.2 流量控制系统

### 3.2.1 流量控制的需求分析

流量控制系统广泛应用于化工、水处理、食品加工等行业，它需要确保物料或液体以一定的速率通过系统。在流量控制系统的设计和实施过程中，需要考虑以下要点：

- 精确度：系统要能准确控制流量，以满足工艺要求。
- 线性：系统控制响应与流量之间的关系应尽可能线性，以简化控制策略。
- 抗扰动：系统应具有良好的抗扰动能力，能抵御来自管道压力波动、温度变化等因素的干扰。

### 3.2.2 PID控制器的设计与实现

在流量控制中，PID控制器的设计与实现和温度控制类似，但是关注的参数是流量而不是温度。以下是实现步骤：

1. 选择适当的流量计来检测管道中的流量。
2. 使用控制器（如微控制器或专用PID控制器）来实现控制算法。
3. 设定PID参数，以便系统能够根据流量的变化及时作出调整。
4. 将控制器的输出转化为调节阀门开度或泵转速等实际操作。

### 3.2.3 案例分析：水处理厂的流量调节系统

一个水处理厂需要控制流入和流出处理设施的水流量，以保证水质和水量的稳定。PID控制系统在这里扮演了关键角色。

具体实现包括：

- 在管道中安装电磁流量计来监测实时流量。
- 使用PLC来处理流量计的数据并执行PID控制算法。
- 利用PID控制器调整出水和入水阀门的开度，保持设定的流量值。
- 在实际操作中，需要对PID参数进行微调，以适应不同的水处理阶段和流量需求。

该系统的工作稳定性对于整个水处理过程至关重要。异常流量可能导致处理效率下降或设备损坏，因此，PID控制系统需要设计得足够鲁棒，能够应对各种突发情况。

## 3.3 位置控制系统

### 3.3.1 位置控制的需求分析

位置控制在如机器人、精密定位设备及装配线等领域中至关重要。在设计位置控制系统时，重点考虑以下方面：

- 精度：系统必须能够以高精度将执行元件移动到指定的位置。
- 响应性：系统需要快速对指令作出响应，以便高效完成任务。
- 抗干扰：执行元件运动过程中可能受到各种干扰，系统应保证定位的准确性和重复性。

### 3.3.2 PID控制器的设计与实现

位置控制的PID控制器设计与实现通常包括以下几个方面：

1. 利用编码器或光栅尺等测量设备获取精确的位置信息。
2. 控制器根据测量的位置值和目标位置值计算偏差，并应用PID控制算法。
3. 输出调节信号给伺服电机或其他驱动装置，使其动作以调整位置。
4. 通过优化PID参数，减少位置偏差，并确保快速且平稳地到达目标位置。

### 3.3.3 案例分析：精密定位平台的位置控制

在半导体制造或光刻领域，精密定位平台要求极高的位置控制精度，以便对芯片或光刻板进行精确定位。一个精密定位平台的PID控制系统可能包括：

- 安装高精度的线性编码器来实时测量平台位置。
- 使用高性能微处理器结合PID控制算法进行位置调整。
- 控制信号通过功率放大器传递给线性驱动器或步进电机。
- 根据位置偏差的反馈，系统自动调整PID参数以达到预期精度。

实现高精度定位的关键在于PID参数的精细化调整，以及对非线性因素的补偿。此外，为了保证系统的稳定性和快速响应，可能需要实现更高级的控制策略，如PID前馈控制或复合控制等。

在以上三个案例中，我们可以看到PID控制在工业自动化中的广泛应用，并且通过调整和优化PID参数，可以满足从温度到流量再到位置的多种工业控制需求。随着工业自动化技术的进步，PID控制器正变得更加智能和高效，但其核心控制原理始终没有改变，仍然建立在比例、积分、微分这三个基本控制作用之上。

# 4. PID控制的高级应用与优化

## 4.1 多变量PID控制

### 4.1.1 多变量控制系统的特点

多变量PID控制主要处理的是具有多个输入和输出（MIMO）的系统。与单变量PID控制不同，多变量控制面对的是更复杂的系统，其中多个控制变量相互影响。在这些系统中，对一个控制变量的调整可能会引起其他变量的变化。例如，在化工行业中，温度、压力和流量可能需要同时控制以达到特定的反应条件。

### 4.1.2 多变量PID控制器的设计与优化

设计一个有效的多变量PID控制器需要考虑的因素包括系统耦合和各控制回路之间的干扰。为了减少这种影响，控制器设计通常采用解耦控制策略。一个常见的方法是将多变量问题分解为一组单变量问题，然后应用常规PID控制器。

在优化方面，对多变量PID控制系统的优化通常使用多目标优化技术，来同时满足多个控制指标，如快速响应、低超调量和良好的抗干扰能力。优化算法可以是遗传算法、粒子群优化或模拟退火算法等。

flowchart TD
    A[开始] --> B[定义多变量控制问题]
    B --> C[进行系统耦合分析]
    C --> D[设计解耦策略]
    D --> E[单变量PID控制回路设计]
    E --> F[多变量PID控制器优化]
    F --> G[选择优化算法]
    G --> H[运行优化算法]
    H --> I[控制器参数微调]
    I --> J[多变量PID控制系统部署]
    J --> K[结束]

### 4.1.3 多变量PID控制器的实现与案例

在实现多变量PID控制器时，需要考虑到各个控制通道间的相互作用，并引入适当的解耦控制逻辑。在工业应用中，多变量PID控制的一个典型应用是在飞行控制系统中，飞机的姿态控制需要同时协调多个通道（如滚转、俯仰、偏航）以保持稳定飞行。

## 4.2 非线性PID控制

### 4.2.1 非线性系统的挑战

非线性系统的行为比线性系统要复杂得多，它们的输出并不与输入成正比。例如，在一个非线性控制系统中，相同大小的控制输入可能会在系统状态不同时产生完全不同的效果。这种特性使得标准PID控制器难以应对非线性系统的行为。

### 4.2.2 非线性PID控制器的设计策略

设计非线性PID控制器需要对系统的非线性特性有深入的理解。一种常用的设计策略是使用增益调度PID控制器，其中PID控制器的参数会根据系统状态的变化而动态调整。另外一种方法是使用自适应控制，其中控制器可以自动调整其参数以应对系统特性变化。

例如，一个典型的非线性PID控制应用是在机器人运动控制中，机器人关节的控制就是一个典型的非线性问题，需要通过复杂的数学模型和算法来实现精确控制。

## 4.3 PID控制的先进优化技术

### 4.3.1 遗传算法在PID参数优化中的应用

遗传算法是一种受自然选择启发的优化算法，它通过模拟生物进化过程来解决优化问题。在PID参数优化中，可以将PID控制器的参数编码为染色体，并使用遗传算法的交叉、变异和选择过程来搜索最优解。这种方法特别适合于那些有着复杂响应曲线和多个局部最优的控制系统。

import numpy as np

def fitness_function(parameter_vector):
    # 这里是一个假设的适应度函数，用于评估PID参数
    # 实际中需要根据系统的具体性能指标来设计
    return np.sum((desired_output - actual_output)**2)

# 遗传算法参数
population_size = 100
num_generations = 50
mutation_rate = 0.01

# 初始化种群
population = np.random.rand(population_size, len(parameter_vector))

# 运行遗传算法优化PID参数
for generation in range(num_generations):
    # 计算每个染色体的适应度
    fitness = np.array([fitness_function(individual) for individual in population])
    # 选择过程
    parents = select_parents(population, fitness)
    # 交叉和变异过程
    population = crossover_and_mutation(parents, mutation_rate)

# 找到最优的PID参数
best_individual = population[np.argmax(fitness)]

### 4.3.2 神经网络在PID控制中的应用

神经网络由于其强大的非线性拟合能力和自学习特性，在PID控制中可以用来在线调整PID参数。神经网络可以接受系统的实时数据作为输入，并输出最优的PID控制参数，从而适应环境和系统动态变化。

### 4.3.3 预测控制与PID控制的结合

预测控制是一种先进的控制策略，它考虑到了系统的未来行为，并据此计算控制输入。将预测控制与PID控制相结合可以形成预测PID控制（Predictive PID Control, PPC），它通过预测模型来预测未来的系统输出，并将此信息反馈到PID控制器中，从而提高控制系统的性能。

在实际应用中，这种结合可以使得PID控制更加预见性，特别是在那些动态变化快和噪声干扰大的系统中，预测PID控制展现出了其独特的优势。

# 5. PID控制系统的故障诊断与维护

## 5.1 故障诊断的必要性

在现代工业自动化系统中，PID控制系统作为关键环节，其运行状态直接影响到整个系统的性能和效率。故障诊断不仅是为了保障系统稳定运行，更是为了及时发现问题，预防潜在的生产事故，以及实现对系统性能的持续优化。了解故障诊断的重要性有助于提前采取措施，减少生产过程中的风险和损失。

## 5.2 常见的PID控制故障类型

PID控制系统的故障类型多种多样，通常可以分为以下几类：

- **传感器故障**：传感器故障是PID控制中最常见的问题之一。传感器的精度降低或完全失效都会导致错误的反馈信号，进而影响PID控制器的调整准确性。

- **执行器故障**：执行器包括电机、阀门等，这些部件的故障会直接影响控制系统的执行能力。

- **PID参数设置不当**：不当的PID参数设置会导致系统响应缓慢、振荡或稳定性差等问题。

- **外部干扰**：各种外部环境因素如温度、湿度变化等，可能对系统产生干扰。

- **通信故障**：在复杂的控制系统中，各个组件间的通信至关重要。通信故障可能包括信号丢失、错误或延迟。

## 5.3 故障诊断的步骤与方法

故障诊断是一个系统性的过程，需要一步步地排查以确定问题所在。以下是一些常见的故障诊断步骤：

- **观察系统行为**：首先监控系统的实际行为，如输出是否达到设定目标、是否存在振荡或者波动等异常现象。

- **检查反馈信号**：比较实际反馈信号与预期信号之间的差异，以识别传感器可能出现的问题。

- **检验PID参数**：通过查看历史记录和调整参数，分析PID控制器的调整是否合理。

- **诊断执行器响应**：查看执行器是否能够准确响应PID控制器的输出，确保执行器工作正常。

- **分析外部干扰和通信状态**：检查外部环境变化，以及通信链路的状态，确保它们不会影响系统。

以下是一个示例代码，用于检测系统输出与设定点之间的偏差：

def check_system_behavior(setpoint, actual_output):
    # 设定阈值，偏差超过阈值则认为存在问题
    THRESHOLD = 0.05
    deviation = abs(setpoint - actual_output)
    if deviation > THRESHOLD:
        print(f"系统输出与设定点偏差较大：{deviation}")
    else:
        print(f"系统运行正常，偏差为：{deviation}")

# 示例设定点和实际输出
setpoint = 100
actual_output = 95

check_system_behavior(setpoint, actual_output)

## 5.4 维护策略与预防措施

为了避免PID控制系统出现故障，采取适当的维护策略和预防措施至关重要：

- **定期校准传感器**：定期对传感器进行校准，以保证测量的准确性和系统的稳定性。

- **执行器的维护**：定期检查和维护执行器，确保其响应迅速且准确。

- **参数优化**：根据系统性能反馈，定期调整PID参数，以适应系统变化。

- **环境控制**：尽可能地减少外部干扰，比如改善设备周围的环境条件。

- **建立通信冗余**：在系统设计时考虑通信的冗余，以避免通信故障导致的系统停机。

通过上述故障诊断步骤和预防措施的实施，可以大大减少PID控制系统故障的风险，确保整个系统的稳定运行和高效生产。