MATLAB数值计算方法：深入浅出，掌握科学计算利器

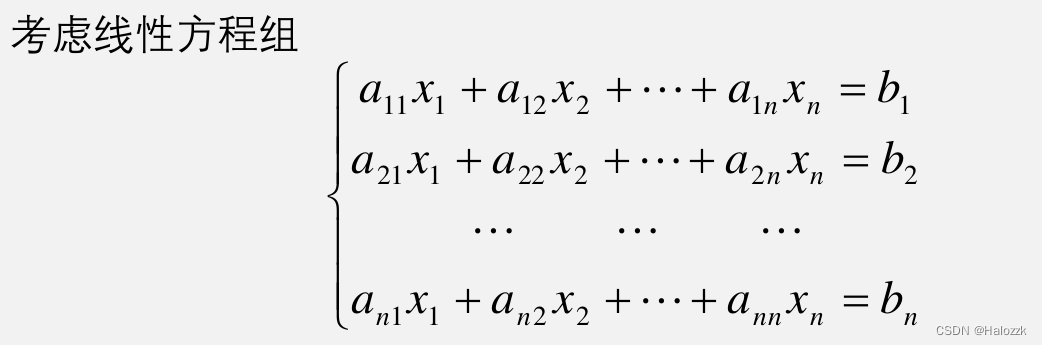
# 1. MATLAB基础**

MATLAB（矩阵实验室）是一种强大的数值计算环境，广泛应用于科学研究、工程和金融等领域。它提供了一系列用于矩阵和数组操作、数据可视化、数值分析和算法开发的函数和工具。

MATLAB 具有直观的语法和交互式开发环境，使其易于学习和使用。它还支持面向对象的编程，允许用户创建自定义函数和类，以扩展 MATLAB 的功能。

# 2. 数值计算基础

数值计算是 MATLAB 的核心功能之一，它提供了一系列强大的工具和算法，用于解决各种科学和工程问题。本章将介绍数值计算的基础知识，包括误差和精度、算法以及 MATLAB 中实现这些算法的函数。

### 2.1 数值计算的误差和精度

#### 2.1.1 误差的类型和来源

数值计算中不可避免地会产生误差，其类型包括：

- **舍入误差：**由于计算机有限的精度，在执行算术运算时会产生舍入误差。
- **截断误差：**当使用近似算法求解问题时，会产生截断误差。
- **数据误差：**由于测量或数据输入错误而产生的误差。
- **算法误差：**由于算法本身的局限性而产生的误差。

#### 2.1.2 精度的控制和优化

控制和优化精度的方法包括：

- **使用更高精度的浮点数：**MATLAB 提供了单精度（`float`）和双精度（`double`）浮点数，双精度具有更高的精度。
- **选择合适的算法：**不同的算法具有不同的精度，选择精度更高的算法可以提高结果的准确性。
- **控制迭代次数：**对于迭代算法，增加迭代次数可以提高精度。
- **使用容差：**在某些情况下，可以设置一个容差，当误差小于容差时停止迭代。

### 2.2 数值计算的算法

MATLAB 提供了各种数值计算算法，包括：

#### 2.2.1 线性方程组求解算法

- **高斯消去法：**一种经典的算法，通过行变换将线性方程组化为上三角形，然后回代求解。
- **LU 分解：**将矩阵分解为下三角矩阵和上三角矩阵，然后分别求解。
- **QR 分解：**将矩阵分解为正交矩阵和上三角矩阵，然后求解。

#### 2.2.2 非线性方程组求解算法

- **牛顿法：**一种迭代算法，通过线性逼近求解非线性方程组。
- **拟牛顿法：**牛顿法的变种，不需要计算雅可比矩阵。
- **共轭梯度法：**一种迭代算法，适用于大型稀疏线性方程组。

#### 2.2.3 插值和逼近算法

- **线性插值：**使用直线连接已知数据点，估计未知点的值。
- **多项式插值：**使用多项式拟合已知数据点，估计未知点的值。
- **样条插值：**使用分段多项式拟合已知数据点，估计未知点的值。

**代码块：**

% 求解线性方程组
A = [2 1; 3 4];
b = [5; 7];
x = A \ b;

% 求解非线性方程组
f = @(x) x^3 - 2*x + 1;
x0 = 1;
x = newton(f, x0);

% 线性插值
x_data = [0, 1, 2];
y_data = [0, 1, 4];
x_query = 1.5;
y_query = interp1(x_data, y_data, x_query);

**逻辑分析：**

- 求解线性方程组：使用 `A \ b` 直接求解。
- 求解非线性方程组：使用牛顿法迭代求解。
- 线性插值：使用 `interp1` 函数进行线性插值。

**参数说明：**

- `A`：系数矩阵
- `b`：常数向量
- `x0`：初始猜测值
- `f`：非线性方程组
- `x_data`：已知数据点的 x 坐标
- `y_data`：已知数据点的 y 坐标
- `x_query`：要估计的未知点的 x 坐标

# 3.1 线性代数计算

### 3.1.1 矩阵运算和分解

MATLAB 提供了一系列强大的矩阵运算和分解函数，可用于解决各种线性代数问题。

**矩阵运算**

MATLAB 支持矩阵的加、减、乘、除等基本运算，以及转置、求逆、行列式等高级运算。

% 创建两个矩阵 A 和 B
A = [1 2; 3 4];
B = [5 6; 7 8];

% 矩阵加法
C = A + B; % C = [6 8; 10 12]

% 矩阵减法
D = A - B; % D = [-4 -4; -4 -4]

% 矩阵乘法
E = A * B; % E = [19 22; 43 50]

% 矩阵转置
A_transpose = A'; % A_transpose = [1 3; 2 4]

% 矩阵求逆
A_inverse = inv(A); % A_inverse = [-2  1; 1.5 -0.5]

% 矩阵行列式
det_A = det(A); % det_A = -2

**矩阵分解**

MATLAB 提供了多种矩阵分解方法，如 LU 分解、QR 分解和奇异值分解 (SVD)。这些分解可用于求解线性方程组、特征值和特征向量等问题。

% LU 分解
[L, U] = lu(A); % L = [1 0; 3 1], U = [1 2; 0 2]

% QR 分解
[Q, R] = qr(A); % Q = [0.5774 -0.8165; 0.8165 0.5774], R = [1.7321 1.4142; 0 0.7071]

% 奇异值分解
[U, S, V] = svd(A); % U = [0.5774 -0.8165; 0.8165 0.5774], S = [2.2361 0; 0 0.7071], V = [0.7071 0.7071; -0.7071 0.7071]

### 3.1.2 特征值和特征向量求解

特征值和特征向量是线性代数中重要的概念，可用于分析矩阵的性质和求解线性方程组。

**特征值**

矩阵的特征值是满足以下方程的标量：

Ax = λx

其中：

* A 是矩阵
* x 是特征向量
* λ 是特征