【PFC电感瞬态响应】：理论计算与实际案例，快速解决设计难题


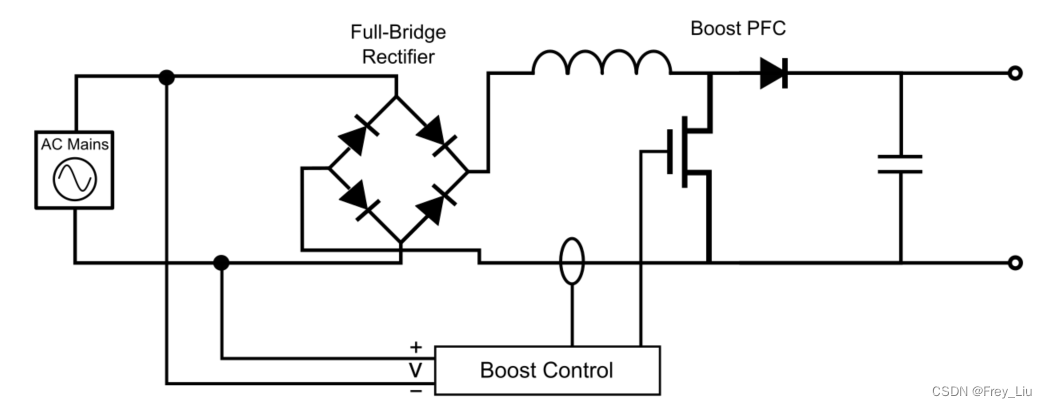
参考资源链接：[Boost PFC电感计算详解：连续模式、临界模式与断续模式](https://wenku.csdn.net/doc/790zbqm1tz?spm=1055.2635.3001.10343)
# 1. PFC电感瞬态响应概述

在现代电力电子系统中，功率因数校正（PFC）电感扮演着至关重要的角色。它不仅影响着系统的能量效率，还决定了电源的瞬态响应品质。PFC电感的瞬态响应特性和其优化策略在保证系统稳定性与可靠性方面不可或缺。

瞬态响应指的是当电力系统经历负载变化或电压波动时，PFC电感所表现出的动态特性。良好的瞬态响应能确保电力系统迅速恢复稳定状态，减少能量损失，并降低对负载的影响。

在本章节中，我们将概述PFC电感的瞬态响应，并引出下一章将深入讨论的理论基础与计算方法。这将为读者建立一个理解PFC电感设计与优化的坚实基础，为后续章节做好铺垫。

# 2. 理论基础与计算方法

## 2.1 PFC电感的工作原理

### 2.1.1 PFC电感在功率因数校正中的作用

功率因数校正（Power Factor Correction, PFC）是电力电子领域的重要技术，主要目的是改善交流电能质量，提高电能利用率。PFC电感是功率因数校正电路中的关键元件之一，它通过储存和释放能量来调整电路的电流波形，使得输入电流波形与电压波形尽量同相，从而提高功率因数。

在交流电路中，电流与电压存在相位差可能导致功率因数下降，而功率因数的下降意味着更多的无功功率需要电网提供。通过在电路中加入PFC电感，可以减少电流和电压之间的相位差，使得更多的有功功率被有效利用，而减少无功功率的消耗。

### 2.1.2 理想与实际电感的行为差异

理想情况下，电感是纯粹的感性负载，它仅存储能量并以磁场的形式释放能量。然而，在实际应用中，PFC电感由于材料、温度、频率等因素的影响，会表现出复杂的阻性和容性特性。

现实中的PFC电感会受到铜损（线圈电阻导致的热损耗）、铁损（磁芯材料引起的损耗）以及漏感（磁场未完全耦合到线圈产生的能量损失）的影响。因此，在设计时需要考虑这些实际因素，以确保PFC电感在预期的频率和温度范围内表现符合预期。

## 2.2 瞬态响应的理论模型

### 2.2.1 电路瞬态分析的基本理论

瞬态响应是指电路在受到瞬时扰动或输入变化时的行为响应，是在一定时间内电流或电压从一个稳态到另一个稳态的过渡过程。在PFC电感的设计中，瞬态响应分析对于确保电路在动态条件下的稳定性和可靠性至关重要。

电路的瞬态分析基于基尔霍夫电压和电流定律，结合电感和电容的特性方程。通过构建和求解线性或非线性微分方程组，可以获得电路在特定初始条件和输入条件下的瞬态行为。这些分析通常需要结合数学软件工具进行。

### 2.2.2 常见电路模型与等效电路分析

为了简化分析，实际电路的复杂性通常通过构建等效电路模型来降低。在PFC电感的瞬态分析中，常用的电路模型包括RC电路、LC串联或并联电路等。这些模型能够模拟电路在瞬态过程中的基本行为。

等效电路通常用来模拟PFC电感在实际工作条件下的性能。例如，使用等效串联电阻（ESR）和等效串联电感（ESL）来表示实际电感的损耗和寄生效应。通过计算等效电路在特定激励下的响应，可以预测PFC电感在电路中的表现。

## 2.3 瞬态响应的数学计算

### 2.3.1 使用微分方程描述瞬态过程

瞬态过程的数学描述一般通过微分方程来表达。在PFC电感的应用中，电流和电压随时间变化的关系可以通过线性或非线性微分方程描述。这些微分方程可以是常微分方程或偏微分方程，具体取决于电路的复杂度和所应用的物理模型。

例如，对于一个简单的LC电路，可以建立以下二阶常微分方程：
\[ V_L(t) + V_C(t) = V_{in}(t) \]
其中 \( V_L(t) \) 和 \( V_C(t) \) 分别为电感和电容两端的电压，\( V_{in}(t) \) 为输入电压。

### 2.3.2 求解微分方程的数值方法

在实际应用中，手工求解复杂的微分方程往往是不切实际的，因此通常采用数值方法进行求解。数值方法如欧拉法、龙格-库塔法（Runge-Kutta）等可以有效地求解初值问题和边值问题。

在PFC电感的瞬态分析中，常见的步骤包括：

1. 将微分方程离散化，将时间轴划分为小的时间步长。
2. 在每个时间步长上应用数值积分方法，迭代求出电流和电压随时间的变化值。
3. 使用迭代方法时，需要设定初始条件，如初始电流和电压值。
4. 根据计算结果绘制瞬态响应曲线，评估电路的动态性能。

下面是一个使用Python进行数值解的简单示例：

import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import odeint

# 定义微分方程组
def circuit_odes(y, t):
    V_in = 10  # 假设输入电压为常量10V
    L = 1e-3  # 电感值1mH
    C = 1e-6  # 电容值1uF
    R = 100   # 电阻值100欧姆
    di_dt = (V_in - y[1]) / L
    dv_dt = y[0] / (C * R)
    return [di_dt, dv_dt]

# 初始条件
y0 = [0, 0]  # 初始电流和电压都为0

# 时间点设置
t = np.linspace(0, 1e-3, 100)  # 从0到1ms的100个时间点

# 解微分方程
solution = odeint(circuit_odes, y0, t)

# 绘图
plt.plot(t, solution[:, 0], label='Current')
plt.plot(t, solution[:, 1], label='Voltage')
plt.legend(loc='best')
plt.xlabel('Time (s)')
plt.grid()
plt.show()

在这个例子中，我们首先定义了一个函数 `circuit_odes` 来表示电路的微分方程组。然后我们使用 `odeint` 函数来求解微分方程组，最后通过matplotlib绘制电流和电压随时间变化的图像。这个简单的脚本可以作为一个起点，用于对更复杂的PFC电路进行瞬态分析。

# 3. PFC电感设计标准与规范

### 3.1 设计要求与规格参数

#### 3.1.1 标准中对PFC电感的要求

在现代电子系统中，PFC电感是实现功率因数校正的关键组件。它需要根据具体的应用场景、电源类型、开关频率以及所需的功率等级来设计。在设计PFC电感时，首要步骤是参考IEEE、IEC等国际标准和特定行业的规范，如EN61000-3-2等，确保设计符合相关电磁兼容（EMC）和电磁干扰（EMI）的规定。

PFC电感的性能直接影响到整个电源系统的效率和稳定性。为了满足这些标准，电感设计必须考虑到诸如额定电流、饱和电流、电感值、品质因数（Q因子）、直流电阻（DCR）、尺寸和成本等因素。例如，一个PFC电感的设计可能需要在高效率和小型化之间寻求平衡，而这些因素都将在电感的性能规格上体现出来。

#### 3.1.2 选取关键参数的原则与方法

在设计PFC电感时，关键参数的选择需要遵循一些基本原则，如效率最大化、温升最小化、成本控制以及对开关电源工作频率的适应性。

- **效率最大化**：选择合适的导线尺寸、磁芯材料和结构可以降低损耗，提高电感的效率。
- **温升最小化**：电感在工作过程中会产生热量，合理的设计可以确保电感在最大工作电流下，其温升低于标准规定的极限。
- **成本控制**