定点数舍入误差：分析舍入方式对定点数计算精度的影响，掌握精度控制的奥秘

# 1. 定点数概述

定点数是一种计算机数字表示形式，它将数字表示为一个固定的小数点位置。与浮点数不同，定点数的小数点位置是固定的，不会随着数字的大小而变化。这使得定点数在某些应用中具有优势，例如需要确定精度或范围有限的应用。

定点数通常使用二进制补码表示，其中最高位表示符号（0表示正数，1表示负数），其余位表示数字的幅度。小数点隐含在最高有效位的右侧，其位置由数据类型决定。例如，一个 8 位定点数可能具有 7 位整数位和小数点后一位。

# 2. 定点数舍入误差的理论分析

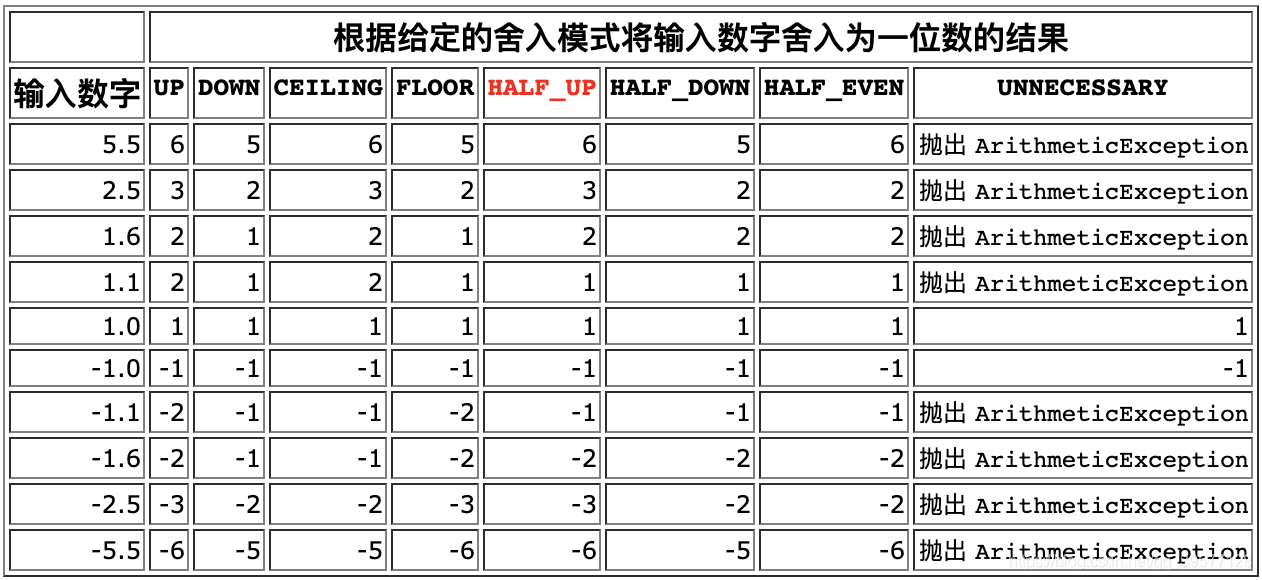
### 2.1 舍入方式对舍入误差的影响

舍入误差是定点数计算中固有的问题，它是由将无限长的实数舍入到有限位宽的定点数表示时产生的。不同的舍入方式会对舍入误差产生不同的影响。

#### 2.1.1 截断舍入

截断舍入是将小数部分直接舍弃，不进行任何四舍五入。这种舍入方式简单易行，但产生的误差可能是最大的。

**代码块：**

def truncate_round(x):
  """截断舍入函数。

  Args:
    x: 待舍入的实数。

  Returns:
    舍入后的定点数。
  """
  return int(x)

**逻辑分析：**

`truncate_round` 函数将输入实数 `x` 直接转换为整数，舍弃小数部分。

#### 2.1.2 四舍五入

四舍五入是将小数部分四舍五入到最接近的整数。这种舍入方式产生的误差一般较小，但可能存在舍入到错误方向的情况。

**代码块：**

def round_half_even(x):
  """四舍五入函数。

  Args:
    x: 待舍入的实数。

  Returns:
    舍入后的定点数。
  """
  return int(round(x))

**逻辑分析：**

`round_half_even` 函数使用 `round` 函数将输入实数 `x` 四舍五入到最接近的整数。`round` 函数采用四舍五入规则，即如果小数部分大于或等于 0.5，则向上舍入；否则，向下舍入。

#### 2.1.3 向上舍入

向上舍入是将小数部分始终向上舍入到最接近的整数。这种舍入方式产生的误差总是正的，但可以保证舍入结果不会比原实数小。

**代码块：**

def ceil(x):
  """向上舍入函数。

  Args:
    x: 待舍入的实数。

  Returns:
    舍入后的定点数。
  """
  return int(math.ceil(x))

**逻辑分析：**

`ceil` 函数使用 `math.ceil` 函数将输入实数 `x` 向上舍入到最接近的整数。`math.ceil` 函数返回大于或等于 `x` 的最小整数。

#### 2.1.4 向下舍入

向下舍入是将小数部分始终向下舍入到最接近的整数。这种舍入方式产生的误差总是负的，但可以保证舍入结果不会比原实数大。

**代码块：**

def floor(x):
  """向下舍入函数。

  Args:
    x: 待舍入的实数。

  Returns:
    舍入后的定点数。
  """
  return int(math.floor(x))

**逻辑分析：**

`floor` 函数使用 `math.floor` 函数将输入实数 `x` 向下舍入到最接近的整数。`math.floor` 函数返回小于或等于 `x` 的最大整数。

### 2.2 舍入误差的量化评估

为了量化舍入误差，可以引入以下度量指标：

####