单片机程序设计中的PID控制实战：打造稳定可靠的系统

# 1. PID控制理论基础

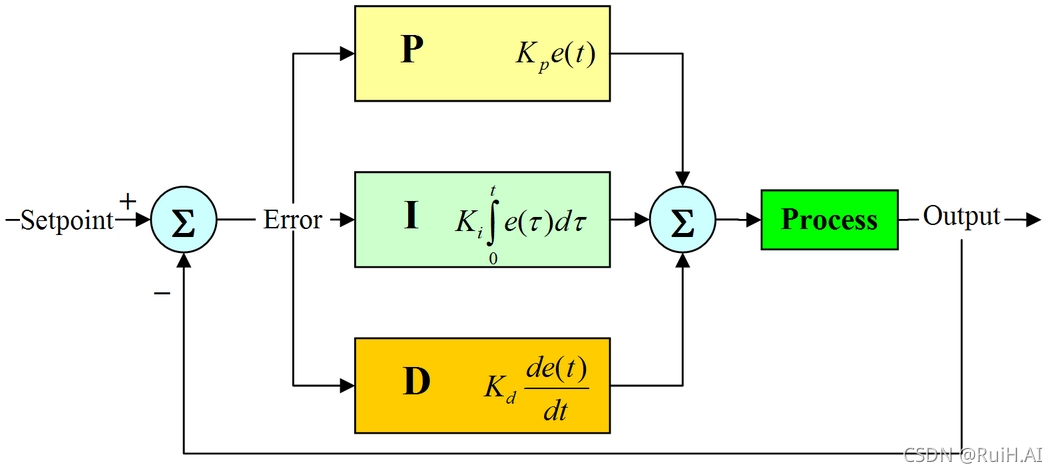
PID控制是一种经典的反馈控制算法，广泛应用于工业自动化、机器人控制等领域。其基本原理是通过测量系统输出与期望输出之间的偏差，并根据偏差大小调整控制信号，从而使系统输出尽可能接近期望输出。

PID算法的数学模型如下：

u(t) = Kp * e(t) + Ki * ∫e(t)dt + Kd * de(t)/dt

其中：

* `u(t)` 为控制信号
* `e(t)` 为系统输出与期望输出之间的偏差
* `Kp` 为比例增益
* `Ki` 为积分增益
* `Kd` 为微分增益

# 2. 单片机PID控制算法实现

### 2.1 PID算法的数学模型

PID算法的数学模型为：

u(t) = Kp * e(t) + Ki * ∫e(t)dt + Kd * de(t)/dt

其中：

- `u(t)`：控制输出
- `e(t)`：误差，即设定值与实际值之差
- `Kp`：比例系数
- `Ki`：积分系数
- `Kd`：微分系数

### 2.2 PID算法的离散化实现

为了在单片机中实现PID算法，需要将其离散化。离散化后的PID算法模型为：

u(k) = Kp * e(k) + Ki * T * ∑[e(i) * T] + Kd * (e(k) - e(k-1)) / T

其中：

- `k`：采样时刻
- `T`：采样周期

### 2.3 PID参数的整定方法

PID参数的整定至关重要，它直接影响控制系统的性能。常用的整定方法有：

- **齐格勒-尼科尔斯法：**该方法基于系统阶跃响应，通过观察系统响应时间和过冲量来确定PID参数。
- **科恩-库恩法：**该方法也基于系统阶跃响应，但通过观察系统响应的上升时间和延迟时间来确定PID参数。
- **经验法：**该方法根据经验和工程实践来确定PID参数，通常用于简单系统或对控制精度要求不高的场合。

### 代码示例

以下代码段展示了离散化PID算法的实现：

def pid_control(error, kp, ki, kd, dt):
  """
  PID控制算法的离散化实现

  参数：
    error: 误差
    kp: 比例系数
    ki: 积分系数
    kd: 微分系数
    dt: 采样周期

  返回：
    控制输出
  """

  # 积分项
  integral = 0
  integral += error * dt

  # 微分项
  derivative = (error - self.prev_error) / dt

  # 控制输出
  output = k