【C语言递归算法深度探索】：计算复杂表达式的计算器开发


参考资源链接：[编写一个支持基本运算的简单计算器C程序](https://wenku.csdn.net/doc/4d7dvec7kx?spm=1055.2635.3001.10343)
# 1. 递归算法的理论基础

递归算法是计算机科学的核心概念之一，它允许算法调用自身来解决问题。这种技术非常强大，但也需要谨慎使用，因为不当的递归可能导致性能问题甚至系统崩溃。本章将带你走进递归算法的世界，从基础理论出发，逐步深入理解其工作原理和设计要点。

## 1.1 递归算法的基本原理

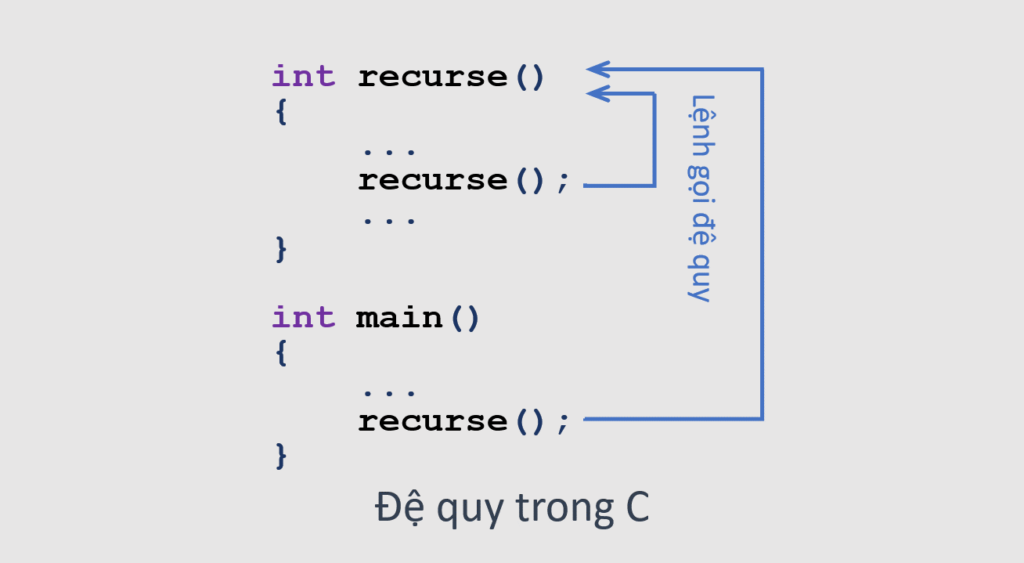
递归算法通过将一个复杂问题分解为相似的小问题，直至到达一个简单的基准情形（base case），然后将小问题的解组合起来形成原问题的解。递归的过程可以用递归函数来实现，每个递归函数都包含两部分：基准情形和递归步骤。

在递归函数中，基准情形负责结束递归调用，防止无限循环；而递归步骤则负责将问题规模缩小，逐步逼近基准情形。理解递归的核心在于把握如何将问题分解以及如何合并子问题的解。

## 1.2 递归与迭代的比较

递归与迭代是解决重复性问题的两种不同方法。迭代方法通常使用循环结构来重复执行代码，直至达到预期结果。而递归则使用函数自身调用自身的方式来实现重复处理。

递归的代码通常更简洁，易于理解和实现，尤其是对于那些天然具有递归性质的问题，如树结构的遍历。然而，递归可能导致较高的内存消耗，因为每一次函数调用都需要在调用栈中保留状态信息。迭代方法通常更加内存高效，但在某些情况下，代码的可读性可能不如递归实现。

理解递归算法的基础知识和与迭代的差异，将为深入学习递归算法的实现和应用打下坚实的基础。在下一章中，我们将探索递归在C语言中的具体实现和设计技巧。

# 2. C语言中的递归函数实现

### 2.1 递归函数的基础知识

#### 2.1.1 递归函数的定义和原理

递归函数在计算机科学中是一种强大的编程结构，它允许函数调用自身以解决问题。这种机制基于数学中的递归定义，其中一个问题可以分解为更小的、形式相似的子问题，直到达到一个简单的基准情形（base case），可以直接解决而不需进一步递归。

从逻辑上讲，一个递归函数包含两个主要部分：

1. **基准情形（Base Case）**：直接解决的最小情况，防止无限递归。
2. **递归步骤（Recursive Case）**：将问题分解为更小的子问题，并调用自身。

递归函数的执行流程可以概括为以下几个步骤：

1. 判断基准情形是否满足，如果满足，则返回基准情形的解。
2. 若不满足基准情形，则执行递归步骤，将问题分解成更小的子问题。
3. 调用自身函数来解决更小的子问题。
4. 将子问题的解合并起来，形成当前问题的解。
5. 返回最终解。

一个经典的递归函数例子是计算阶乘的函数：

int factorial(int n) {
    if (n <= 1) {
        return 1;  // 基准情形
    } else {
        return n * factorial(n - 1);  // 递归步骤
    }
}

在上述代码中，`factorial` 函数首先判断参数 `n` 是否小于等于 1，若是，直接返回 1（基准情形）。否则，函数返回 `n` 与 `n-1` 的阶乘的乘积（递归步骤）。

#### 2.1.2 递归与迭代的区别

递归和迭代是解决重复性问题的两种不同方法。两者在某些情况下可以相互替代，但各自有其优缺点。

- **递归：**
- **优点：** 代码通常更简洁，易于理解和实现。对问题的表达自然，容易看出算法的逻辑结构。
- **缺点：** 需要额外的内存来保存每次函数调用的上下文信息，可能导致栈溢出；通常效率低于迭代方法。

- **迭代：**
- **优点：** 通常需要更少的内存，执行效率高；避免栈溢出的问题。
- **缺点：** 对复杂问题来说，实现可能较为复杂，代码可读性可能下降。

以计算阶乘为例，迭代方法的实现如下：

int factorial_iterative(int n) {
    int result = 1;
    for (int i = n; i > 1; --i) {
        result *= i;
    }
    return result;
}

在这个迭代版本中，通过使用一个循环来重复乘以递减的数，直到达到 1，避免了递归的栈开销。然而，在理解算法逻辑上，递归版本通常被认为更直观。

### 2.2 递归函数的设计技巧

#### 2.2.1 基准情形的重要性

基准情形是递归函数设计中的关键组成部分，它保证了递归能够在有限步骤内终止，防止了无限递归的发生。基准情形通常是问题的最简单实例，可以直接解决而不需要进一步分解。

设计基准情形时应考虑以下几点：

- **完整性**：确保所有的基本情况都被考虑到，没有任何遗漏。
- **最小性**：基准情形应当是问题可以解决的最小子集，避免过早地终止递归。
- **正确性**：基准情形的解应该是正确的，为递归解提供正确的出发点。

举一个例子，计算斐波那契数列的第 `n` 项：

int fibonacci(int n) {
    if (n <= 1) {
        return n;  // 基准情形
    } else {
        return fibonacci(n - 1) + fibonacci(n - 2);  // 递归步骤
    }
}

在这个函数中，基准情形是 `n` 小于等于1的情况，直接返回 `n`。

#### 2.2.2 递归步骤的构造方法

构造有效的递归步骤是递归函数设计的另一个核心部分。这通常涉及到将问题分解成更小的子问题，并且这些子问题与原问题有相同的结构，允许相同函数对它们进行处理。

在构造递归步骤时，应遵循以下原则：

- **子问题的规模**：子问题应比原问题规模小，但结构相同，这样可以保证递归能逐渐接近基准情形。
- **问题分解的策略**：选择合适的策略将大问题分解为小问题，常见的策略有：减治、分治、变治等。
- **解的合并**：在返回上一层递归之前，需要有一个逻辑来合并子问题的解，形成当前问题的解。

举例，考虑二分搜索算法：

int binary_search(int arr[], int left, int right, int x) {
    if (right >= left) {
        int mid = left + (right - left) / 2;
        if (arr[mid] == x) {
            return mid;  // 基准情形
        }
        if (arr[mid] > x) {
            return binary_search(arr, left, mid - 1, x);  // 递归步骤
        }
        return binary_search(arr, mid + 1, right, x);  // 递归步骤
    }
    return -1;  // 未找到
}

在这个例子中，递归步骤是将数组的搜索区间缩小一半，直到找到目标元素或区间为空。

### 2.3 递归函数的性能考量

#### 2.3.1 递归深度的影响

递归深度指的是递归调用的最大层数，这与栈内存的使用息息相关。每个函数调用都会在栈上分配一定的内存空间，用于保存函数的参数、局部变量以及返回地址等信息。随着递归深度的增加，所需的栈空间也增加。在某些情况下，当递归深度过大时，可能会超出栈的大小，导致栈溢出错误。

为了确保递归程序的稳定性，需要合理控制递归深度：

- **优化递归算法**：通过减少递归次数或改用迭代方法降低递归深度。
- **增加栈空间**：在某些系统上，可能可以通过增加栈的大小来防止栈溢出。
- **尾递归优化**：编译器可以优化尾递归形式的递归函数（函数的最后一个操作是递归调用），将其转换为迭代形式，减少栈空间的使用。

一个简单的例子来说明递归深度的影响：

int recursive_sum(int arr[], int n) {
    if (n == 0) {
        return 0;
    } else {
        return recursive_sum(arr, n - 1) + arr[n - 1];  // 每次递归调用都会增加栈深度
    }
}

#### 2.3.2 递归效率的优化策略

递归函数在执行效率上往往不如迭代算法，主要是因为递归调用涉及额外的栈操作。为提高递归函数的效率，可以考虑以下优化策略：

- **记忆化（Memoization）**：存储已经计算过的子问题结果，避免重复计算。
- **尾递归优化**：将递归函数转换为尾递归形式，以便编译器优化。
- **循环展开**：手动地将递归逻辑转换为迭代逻辑，减少函数调用的开销。

例如，考虑计算斐波那契数列的第 `n` 项的优化版本：

int fibonacci_memoization(int n, int *memo) {
    if (n <= 1) {
        return n;
    } else if (memo[n] != -1) {
        return memo[n];  // 使用记忆化的结果
    } else {
        memo[n] = fibonacci_memoization(n - 1, memo) + fibonacci_memoization(n - 2, memo);
        return memo[n];
    }
}

在这个优化版本中，我们使用了一个数组 `memo` 来存储已经计算过的斐波那契数，以避免重复计算。

通过上述优化措施，可以显著提高递归算法的性能，减少不必要的资源消耗，并保证程序的稳定性。在下一章节中，我们将深入探讨递归在表达式解析和计算器开发中的应用。

# 3. 表达式解析与计算

## 3.1 表达式求值问题的定义

表达式求值是计算机科学中的一个基础问题，它涉及到将一系列